NLP复习之朴素贝叶斯
朴素贝叶斯分类器和加一平滑计算每个单词的似然值
贝叶斯规则:c表示类别,d表示数据
例题1
假设句子“I always like foreign films.”中每个单词对应每个类的似然估计如下,请判断该句子属于正面还是负面评论。
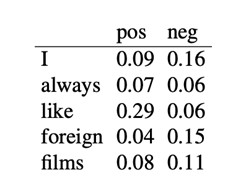
解
似然估计:
先验概率
后验概率
所以显然是负面评论
例题2
给出以下包含五个文档的训练集,每个文档都标记为不同的类型:comedy或action,
\1. fun, couple, love, love comedy
\2. fast, furious, shoot action
\3. couple, fly, fast, fun, fun comedy
\4. furious, shoot, shoot, fun action
\5. fly, fast, shoot, love action
请使用朴素贝叶斯分类器和加一平滑,计算每个单词的似然值,并判断新文档 – “fast, couple, shoot, fly”的类型。
解
先验概率
comedy中单词总数为:
action中总数为:
最大似然
其他同理
则后验概率
例题3
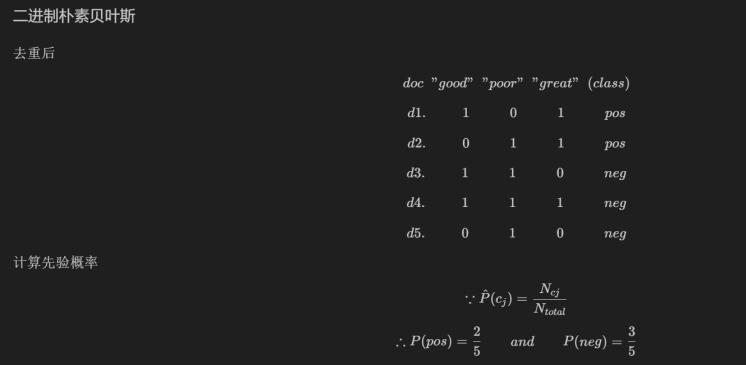
根据下面包含五个已标记的文档数据集(每个文档使用了情感词汇进行特征表示,例如的d1中包含3个good和3个great,且对应的类别为positive),使用加一平滑分别训练多项式朴素贝叶斯和二进制朴素贝叶斯两个模型。(二进制去重)
| doc | good | poor | great | (class) |
|---|---|---|---|---|
| d1 | 3 | 0 | 3 | pos |
| d2 | 0 | 1 | 2 | pos |
| d3 | 1 | 3 | 0 | neg |
| d4 | 1 | 5 | 2 | neg |
| d5 | 0 | 2 | 0 | neg |
使用训练好的两个朴素贝叶斯模型对句子“A good, good plot and great characters, but poor acting. ”进行分类。

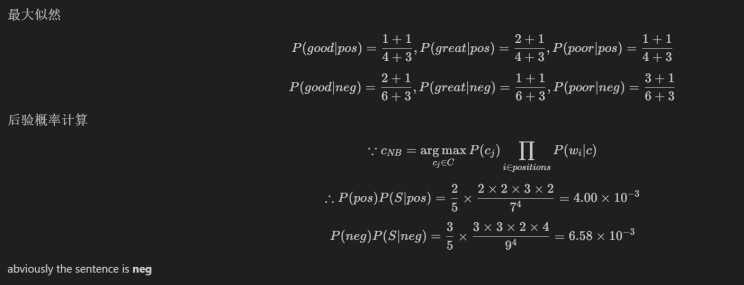
本文作者:拂云堂 诩言
本文链接:https://www.cnblogs.com/wanyy-home/p/17926127.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步