NLP复习之N元文法
N元文法的统计
二元概率方程：
\[P(w_n|w_{n-1}) = \frac{C(w_{n-1}w_n)}{C(w_{n-1})}
\]
三元概率估计方程：
\[P(w_n|w_{n-2},w_{n-1}) = \frac{C(w_{n-2;n-1}w_n)}{C(w_{n-2;n-1})}
\]
例题1
给出以下一个小型语料库，在最大似然一元模型和二元模型之间使用加一平滑法进行平滑, 请计算P(Sam|am)。注意要将tokens 和与其他单词一样看待。
<s> I am Sam </s>
<s> Sam I am </s>
<s> I am Sam </s>
<s> I do not like green eggs and Sam </s>
解
\(P(Sam|am) = \frac{C(am;Sam)}{C(am)} = \frac{2}{3}\)
\(P_{Laplace}(Sam|am) = \frac{C(am;Sam)+1}{C(am)+|V|} = \frac{2+1}{3+11} = \frac{3}{14}\)
注意：V是不同单词的种类！！是词汇表的大小
例题2
在1的条件下，请使用线性插值法，其中假设 λ1 = 1/2， λ2 =1/2，请计算P(Sam|am)。注意要将tokens 和与其他单词一样看待。
解
注意：S是单词出现的总次数！！
统计\(bigram\)数量，\(P(Sam|am) = \frac{3}{14}\)
根据线性插值法，
\[\begin{aligned}
P(Sam|am) &= \lambda_2 \times P(Sam|am) + \lambda_1 \times P(Sam)\\
&= 0.5 \times \frac{3}{14} + 0.5 \times \frac{4}{25} \\
\end{aligned}
\]
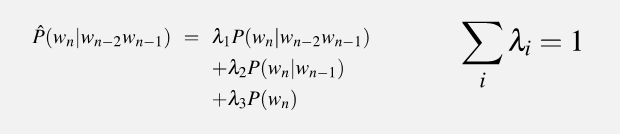
例题3
给定一个包含 100 个数字的训练集，其中包含 91 个0和 1-9 其他数字中的每个数字。 有以下的测试集：0 0 0 0 0 3 0 0 0 0。计算该问题的一元困惑度 unigram perplexity。
困惑度
\[PP(W) = P(w_1w_2 \dots w_N)^{-\frac{1}{N}}
\]
困惑度越小，概率越大。
解
\(P(0) = 91 / 100 = 0.91;\)
\(P(1;9) = 1 / 100 = 0.01;\)
\(PP(W) = (P(0)p(0)p(0)p(0)p(0)p(3)p(0)p(0)p(0)p(0))^{-0.1} = 1.725\)
