深度学习小记

深度学习小记

0 前言

近段时间，由于工作需要，一直在看深度学习的各种框架，主要是Caffe和Tensorflow。并且在可预见的未来，还会看更多不同的深度学习框架。最开始我是以软件工程师的角度去阅读这些框架的，说实话，Caffe的代码框架逻辑清晰相对好理解一点，而TensorFlow就比较麻烦了，里面内容太多，函数调用链非常长，且使用了大量的C++11语法，这对于C++功底不好的我来说无疑是重大打击...因此，我必须跳出软件工程师的思维，以算法工程师的视角来审视这些框架。考虑到它们都是为深度学习服务的，因此我转而去思考深度学习的本质，希冀能够触类旁通。

鉴于深度学习与神经网络的关系类似于漂移与汽车的关系。深度学习可以理解成用(深度)神经网络来进行机器学习，漂移可以理解成用汽车来做一些风骚的走位操作。因此，我的思考重点又聚焦到神经网络身上。网上对神经网络的解释非常多，但一般都是直接扔给你一大堆陌生的名称以及一堆看起来就很烦的公式，配合上他们说教的语气，给人的感觉就是：你看，神经网络就这么简单，你现在一脸懵逼觉得复杂是因为你没我厉害，跟着我学几年也许你就会了。

不可否认，这些专有名词和公式非常重要，但是我们也必须知道所有的名词和公式都是数学家为了方便运算/记录，而对某些概念或者规则进行的抽象处理，因此我们应该先理解这些名词或公式背后的概念或规则，然后再来反推这些公式，这才是最合理的学习方式。那么这么多名词与公式，我应该从哪入手呢？即在整个神经网络中哪个概念是最重要、最核心的呢？冥思良久，Tensorflow这个单词给了我答案。它可以拆分为Tensor + flow，显然在Google看来基于神经网络的深度学习框架本质上就是：像车间流水线一样对各种Tensor进行处理。好，那么我们就以Tensor为入口探究深度学习的本质。

1 Tensor介绍

Tensor译作“张量”(可能是为了展示它同向量、矩阵之间的联系吧)，但说实话，我完全无法从它的中文名字中理解到它的含义，因此本文就直接使用它的英文名了。Tensor是众多深度学习框架中的一个核心组件(可能其他框架中不叫Tensor，比如caffe中叫做Blob，但其内在含义都一样，所以我们完全可以将caffe叫做Blobflow)，后续几乎所有的操作和运算都是基于Tensor进行的。本章将会从Tensor的起源开始，逐步添加各个领域的一丁点知识来阐述我对Tensor在深度学习领域的理解。我可以保证，绝对不会有一个公式。

1.1 一点点数学、物理领域的知识

在了解Tensor之前，我们需要简要回顾一下在高中/大学时学过的另外3个重要数学概念：scalar(标量), vector(向量), matrix(矩阵)。

1. scalar(标量): 一个标量就是一个单独的数，一般用小写的变量名称表示，我们也可以将标量看成是零维数组。
2. vector(向量): 也叫矢量，相对于标量而言，它既有大小，又有方向，我们可以将之看做一维数组。
3. matrix(矩阵): 将矩阵拆开来看，它其实就是一列“行向量”，或者一行“列向量”的组合，我们可以将矩阵看做是一个二维数组。

那么Tensor跟它们三个有什么关联或者不同呢？有人说Tensor就是向量和矩阵的扩展，通俗一点，可以将标量视作零维Tensor，向量视作一维Tensor，矩阵视作二维Tensor...看起来是那么回事，但其实错得离谱！因为它将Tensor最本质的特性给丢掉了！

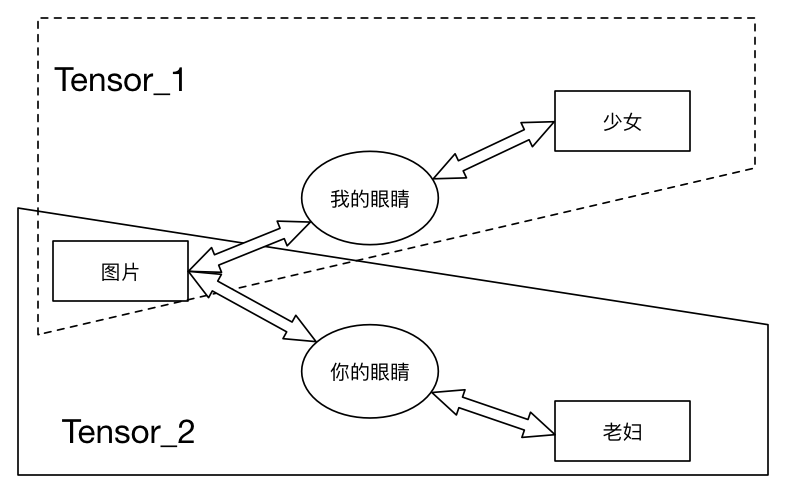
追本溯源，Tensor其实是物理学家提出的一个概念，主要用于描述“物理定律不随着参考系变化的这一性质”——A tensor is something that transforms like a tensor。而后再由严谨的数学家进一步加以抽象和发展，懂了么？呃....等等，怎么感觉越解释越抽象了？下面我们开始说人话，请观察下面一张图：

你看到的是老妇还是少女？不同的人以不同的方式去观察这张图片，会给出不同的描述。就我而言，看到的是：一位背侧我们的少女，少女的脖子上有一串项链，一头飘逸的长发半遮她的耳朵。而其他人可能看到的是：一位老妇的侧面，少女的耳朵变成了老妇的眼睛，少女的项链变成了老妇的大嘴~

那么现在我问你，无论我们得出的结论是老妇还是少女，它是不是描述的同一幅图片？答案是肯定的，只是由于我们观察的方式不同，而得出了不同的结论而已，且这些不同的结论并没有对错之分，它只表示按照我们的方式看来就是得出这样的结论。回看前文提及的物理学家对Tensor的描述，我们能明显找到两者的共通性：这幅不变的图片就是“不变的物理定律”，而不同的人采取了不同的观察方式其实就是“选用不同的参考系”，他们得出的结论本质上没有对错高下之分。那么我现在说：正如下图所示，Tensor就是这幅不变的图片在不同观察方式下得出的描述，你能理解了么？

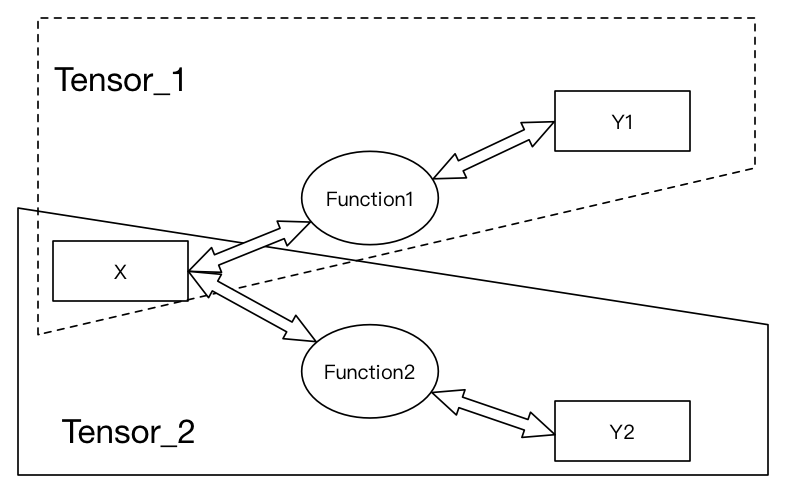
下面再来看看数学家是怎么描述Tensor的。在线性代数中通常有这种说法：矩阵的意义是线性变换，相似矩阵是同一个线性变换在不同基下的表示。划重点，这里的“同一个线性变换在不同基下的表示”不就说的是Tensor么！显然，在数学家眼中，Tensor已经被抽象成了线性变换，如果我们将线性变换看做一个函数的话，正如下图所示：

至此，Tensor在数学上的含义我们就不再展开了，因为这已经足够我们理解深度学习中Tensor的意义。

1.2 一点点生物学领域的知识

这里我们只需要简单理解生物学里面的视觉感知系统就好。先看几组动物与人类在视觉感知上的差异对比图：

1 苍蝇与人类的视觉感知差异：

​ 左边是人的视觉感知，右边是苍蝇的视觉感知

2 蛇与人类的视觉感知差异：

更多的视觉差异对比见这里。

通过上面的对比图可以知道，即便是相同的场景，经过不同的视觉系统，也会得到不同的感知。用生物学上的解释就是：生物所看到的镜像并非世界的原貌，而是长期进化出来的适合自己生存环境的一种感知方式。也就是说：

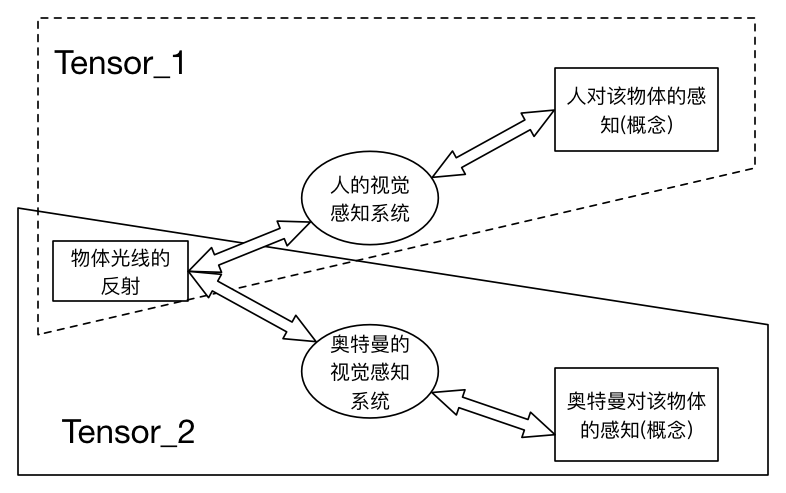
物体光线的反射 -> 某生物的视觉感知系统进行各种处理 -> 产生该生物脑中对该物体的感知(概念)——正如上图所示。这跟Tensor在物理、数学上的定义是不是非常相似呢？所以说，目前在深度学习领域用得最广最成熟的图像识别技术，其本质上并不是识别这个图像在客观上是什么，而是不停地训练该识别系统，以到达模拟人类视觉感知的程度。因此，当你发现自己的图像识别系统总是识别错误的时候，也不用惊慌，因为你可能刚好训练出了M8星云奥特兄弟们的视觉感知，而不是人类的视觉感知，如果踩了狗屎运你们的业务方又刚好是奥特兄弟的话，那么也算是圆满完成项目了^_。

同样的，我们可以将之推广到模拟人类听觉感知系统的语音识别等等。正是基于此，早期的神经网络也称之为“(多层)感知机”。

1.3 一点点数字图像领域的知识

数字图像一般分为“位图”和“矢量图”。位图是由“点阵”组成的，计算机在存储或处理位图的时候是处理这个“点阵”，每个点描述的是该位图中一个像素点的灰度；而矢量图是由线条和填充于线条所围成的区域之中的灰度组成的，计算机记录如何绘制这些图形，而不记录“点阵”。这里我们只关心位图。以最简单的灰度图(就是大家所谓的黑白图片)为例，比如一张400 x 400像素的灰度图，其本质上就是一个400x400的矩阵，矩阵中每个元素就是一个像素点。每个元素取值0~255之间的整数，代表256种灰度等级。灰度值越大，像素的颜色越‘白/浅’；灰度值越小，像素的颜色越’黑/深‘。比如下图字符8的图像以及其对应的灰度值矩阵表示如下：

那么彩色图片在计算机中是怎么表示的呢？以常用的RGB图片为例。RGB是一种数字图像颜色模型，其中R代表Red红色，G带便Green绿色，B代表Blue蓝色。我们可以简单地将之理解为：RGB就是以红绿蓝三原色的组合来展示一张彩色图像。如下面这张经典的图片所示(为描述方便，假设为400x400像素的RGB图片)：

其实它是由3个分别在红、绿、蓝颜色上的灰度图组合渲染而成:

如你所见，每一种原色(也叫分量)单独看都是一个400x400的灰度图片，对应一个400x400的矩阵，因此这张RGB图本质上就是一个400x400x3的三维数组。好了，关于数字图像的一点点知识我们就浅尝辄止地介绍到这里了，更详细的信息可以参考这里。细心的读者可能发现本节一直使用矩阵而非Tensor，那是因为在数字图像领域人们会更直观地将每张图片理解成n维数组，而非Tensor。

下面我将直接告诉你，其实这些n维数组正确的称呼就应该是“n维Tensor”! 回顾一下Tensor的概念，里面有个非常关键的信息——“观察方式”或者“参考系”或者某种规则。试想如果我直接将字符8的灰度值矩阵图扔给你，你能脱口而出它是字符8么？显然是不能的，我们只有将它交给计算机按照约定的规则渲染成字符8的位图之后，你才能知道这个灰度值矩阵真正的含义。因此在数字图像领域，其“参考系”或者“观察方式”是隐式地定义在灰度值Tensor内部的，我们只有使用事先约定好的规则才能正确地表示这些Tensor的图像含义。因此，当以后使用深度学习处理图像数据的时候，请叫它们Tensor而非数组或者矩阵。

1.4 小结

通过前面的介绍，我相信你肯定对Tensor有了一个比较直观的理解。本质上Tensor就是对某个事物按照不同观测方式得出的描述结论。不过每次都这么描述Tensor总是比较麻烦，因此人们为了方便，就将得出的“描述结论”称之为Tensor，而不再显式提及该“描述结论”对应的“观测方式”了，但是我们必须在内心时刻谨记Tensor真正的含义。比如将“少女”， “老妇”称之为Tensor；又例如在数字图像领域，我们约定使用一个3维的Tensor来表示一张RGB图片。下面我们将探讨为什么Tensor是各种以神经网络为基础的深度学习框架中最核心的组件。

2 解剖基于神经网络的深度学习框架

2.1 神经网络与Tensor

我们首先来看一下经典的用于识别0~9手写字符的3层神经网络长什么样：

是不是很复杂？那我把它简化一下，比如只识别1个字符的3层神经网络：

还有点复杂？那我们再进一步简化，比如输入、输出和中间层都只有一个结点的神经网络：

现在再回顾一下我们在第1章中反复画出的Tensor图，它们是不是非常像呢？这里我们可以列举出三点共性：

1. 每一个圆形结点都代表对某个Tensor的一种处理操作，也可以称之为感知；

2. 圆形结点与圆形结点之间只传递Tensor；

3. 都是有向无环图，就跟工厂的流水线一样，有明确的输入和输出，且Tensor的流动路径固定。

   我猜测这就是为什么叫Tensorflow而不叫TensorCircle或者其他名字的原因吧^_~

基于上述分析，我们可以得出结论：神经网络其实就是像流水线一样对输入Tensor依次进行一系列地处理，最终得出我们想要的那个Tensor(结论)。

2.2 深度学习与Tensor

以大名鼎鼎的2012年Imagenet比赛冠军的深度学习模型Alexnet为例

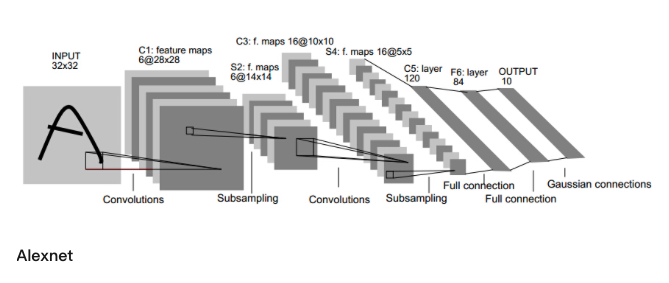
其网络结构图如下：

看起来非常复杂，甚至已经由二维平面架构衍生到了三维立体架构，但它仍然满足我们在2.1章节总结出的三点共性。因此它本质上还是：对输入Tensor依次进行一系列有向无环图的处理，最终得出我们想要的Tensor!

2.3 深度学习及其框架剖析

从前文的分析我们得出了一个结论：深度学习就是对输入Tensor依次进行一系列有向无环图的处理，直至最终得出我们想要的Tensor。大家可能会觉得这个结论不严谨，因为它看起来只描述了深度学习一半的性质——即推理(Inference)部分的性质。所谓的推理就是我们使用已经学习/训练好的可以完成某个功能/任务的模型，对输入Tensor按照既定顺序逻辑进行处理，直至得到该模型的输出Tensor。而深度学习另一个重要的学习/训练性质并没有在这个结论中得到体现。事实是这样的么？其实在训练阶段也是同样的思路，只不过Tensor发生了改变以及Tensor流动的方向相反了而已：使用反向传播算法根据训练结果的误差Loss_Tensor来进行一系列处理，直至训练出满足我们要求的Weight_Tensor以及Bias_Tensor等等。如下图所示：

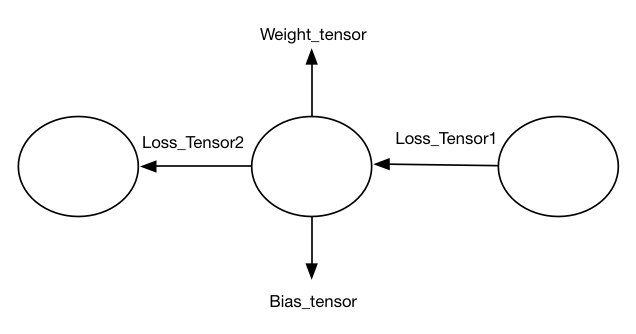
至此，我们已经发掘出深度学习的三个核心要素：

1. 代表数据的Tensor；
2. 代表Tensor流动方向，即Tensor处理序列的有向无环图；
3. 代表对Tensor进行各种处理的圆形结点。

而目前所有的深度学习框架刚好都是以这三个核心要素为出发点进行的架构设计！比如在Caffe中，使用了一个叫做Blob的类来描述Tensor并以数组的形式进行存储，使用了一个Net类来描述Tensor处理序列的有向无环图，使用了各种Layer类来描述对Tensor进行的各种处理，既包括用于推理的正向forward也包括用于训练的反向backward，至于其他的各种类都只是作为后勤工作者来辅助它们而已；同样的在Tensorflow中，使用Tensor类来描述Tensor，使用Graph类来描述Tensor处理序列的有向无环图，使用各种Operation类来描述对Tensor进行的各种处理，而其他的类也都是辅助类，只不过Tensorflow为了方便算法工程师进行模型训练而开发了非常非常多的辅助类而已。有了这个认知，以后再去阅读其他深度学习框架的源码，就容易很多了，甚至我们也可以自己尝试编写一个深度学习框架。

注意：RNN循环神经网络其也是一个有向无环图，只是因为它引入了时间维度，为了描述方便才在其网络图中画出了环而已，为了避免混淆，你也可以将RNN称作“递归神经网络”。

3 总结

古人云，大道至简。深度学习的核心原理是如此之简单，也是让我一时难以置信。不过简单的东西其优缺点也是非常明显的：

优点：理论基石稳固，不容易被推翻，君不见现在各种深度学习网络架构层出不穷，但都逃不出我们总结的三个核心要素么？

缺点：简单的理论要想用于解决复杂的问题，往往需要付出很多额外的代价，也许这就是深度学习不得不依赖于大量有效数据的原因吧。

最后，要想真正看懂在深度学习框架中各种眼花缭乱operation操作，我们还必须去深入研究各种算法，比如反向传播算法、卷积的原理等等，这些内容后续再慢慢补充吧。

4 参考链接

Tensor(张量)的介绍
视觉感知的介绍
RGB图像的介绍
RNN介绍
Neural Networks And Deep Learning
AlexNet的介绍
Caffe框架
Tensorflow框架