无向图的最小环问题 —— AcWing 344.观光之旅

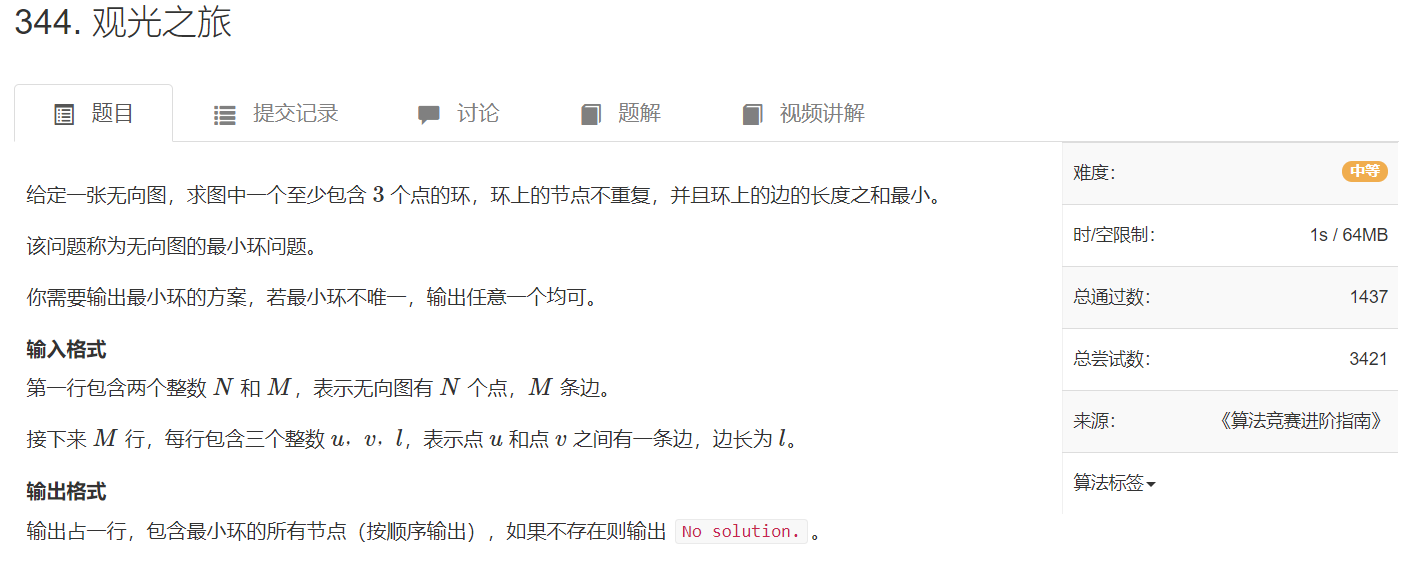
求图上的最小环问题可以用Floyd算法。
Floyd的实质是dp，状态表示为从i ~ j的路径中经过的最大的节点编号是k的路径的最小值是多少，那么我们可以在这过程中利用上一层的状态求出i ~ j的环中经过的节点的最大编号是k的环。
我们可以知道所有的环都可以表示为 i ~ j ~ k ~ i，i ~ j之间的最大的节点编号是k - 1，所以我我们就可以利用三角不等式来求得最小环，同时我们需要维护一下路径顺序，这个环可以等价为k ~ i ~ j ~ k，所以我们就可以先把k和i加到路径中然后递归加入i ~ j之间的路径最后再把j加进去就行了。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <vector>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 110, INF = 0x3f3f3f3f;

int n, m;
int d[N][N], g[N][N]; // g原数组,d最短路径的数组
int p[N][N]; // 从i ~ j的最短路径经过的最大的点是哪个
int path[N];
int cnt;

void get_path(int i, int j) 
{
    int k = p[i][j];
    if (k == 0) return;
    
    get_path(i, k);
    path[cnt ++ ] = k;
    get_path(k, j);
}

int main() 
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= n; i ++ ) g[i][i] = 0;

    while (m -- ) 
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    LL res = INF;
    memcpy(d, g, sizeof g);
    for (int k = 1; k <= n; k ++ ) 
    {
        for (int i = 1; i < k; i ++ ) // 枚举经过环上的最大的点是k - 1的路径长度
            for (int j = i + 1; j < k; j ++ ) // 只用枚举一半就好了,d[i][j]是等价于d[j][i]
                if (res > (LL)g[i][k] + g[k][j] + d[i][j]) 
                {
                    res = (LL)g[i][k] + g[k][j] + d[i][j]; 
                    // 由于我们i ~ j之间得最短路径经过的是k - 1,则要使环上的最大节点是k
                    //那么就必然是原数组从i ~ k + k ~ j之间得最短路径经过的是k。
                    cnt = 0;
                    path[cnt ++ ] = k;
                    path[cnt ++ ] = i;
                    get_path(i, j);
                    path[cnt ++ ] = j;
                }

        for (int i = 1; i <= n; i ++ ) 
            for (int j = 1; j <= n; j ++ ) 
                if (d[i][j] > d[i][k] + d[k][j]) // 如果最短路径上只有两个点的话,由于Floyd的特性,并不会更新p数组
                {
                    d[i][j] = d[i][k] + d[k][j];
                    p[i][j] = k;
                }
    }
    
    if (res == INF) puts("No solution.");
    else for (int i = 0; i < cnt; i ++ ) cout << path[i] << ' ';
    
    return 0;
}