AcWing 171.送礼物

DFS双向搜索的经典例题。

对于DFS和BFS来说双向搜索都能有效降低时间复杂度，但缺点就是会多开销空间，也就是用空间换时间。

由于我们的搜索范围是逐步扩大的所以当我们的每个节点的子节点较多时就可以做到如下:

 

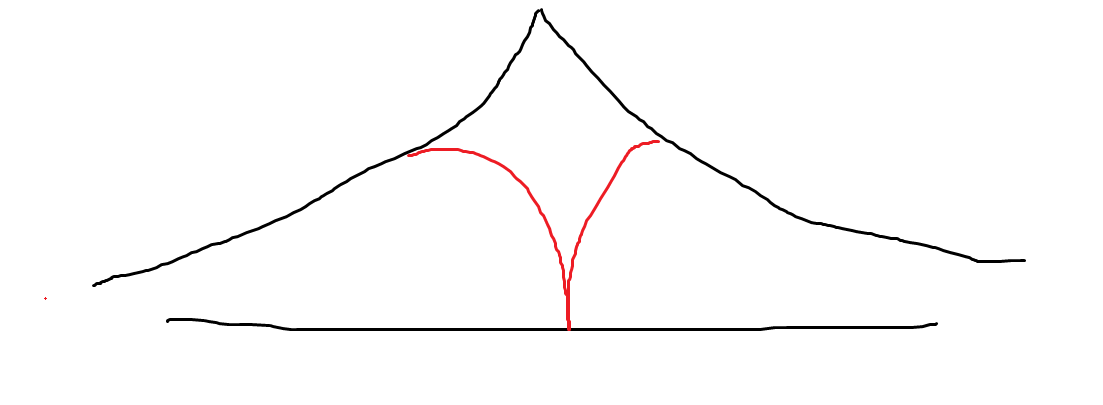
 红色部分是从反向开始搜索，这样我们就可以明显看出我们有效的降低了时间的复杂度。

题目：

 思路：

先通过对前部分进行搜索预处理出来能拿到的重量的所有情况，由于只搜索的一半的物品所以我们的时间复杂度有 2^^N 降低到了2^{^N/2} ,显著降低了时间复杂度，并且进行打表，之后再对后半部分进行搜索时直接进对搜索出来的值在表中进行二分查找到最大的小于 m 的值并且更新一下答案即可。

剪枝：

①：优化搜索顺序

我们需要对后半部分进行二分查找所以时间复杂度为 2^{^N/2} * log^N/2，那么我们可以适当的增加前面的搜索数据减小后面的搜索数据可以均匀一下，这样我们可以对前面的搜索N / 2 + 2 时时间复杂度最为低，而又由于我们增加了前面的搜索数据，这样我们可以将数据从大到小排序，那么我们搜索前面时会优先搜索到大的部分，会减掉更多的大于m的部分枝叶。

②：可行性剪枝

对于大于m的部分枝叶直接减掉不进行搜索。

代码：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 46;

int n, m, res;
int g[N];
int w[1 << 25];
int cnt;

void dfs1(int u, int sum) 
{
    if (u == n / 2 + 2)
    {
        w[cnt ++ ] = sum;
        return;
    }

    dfs1(u + 1, sum);
    if ((LL)sum + g[u] <= m) dfs1(u + 1, sum + g[u]);
}

void dfs2(int u, int sum) 
{
    if (u == n)
    {
        int l = 0, r = cnt - 1;
        while (l < r) 
        {
            int mid = l + r >> 1;
            if (w[mid] + (LL)sum <= m) r = mid;
            else l = mid + 1;
        }
        res = max(res, sum + w[l]);
        return;
    }

    dfs2(u + 1, sum);
    if ((LL)sum + g[u] <= m) dfs2(u + 1, sum + g[u]);
}

int main()
{
    cin >> m >> n;
    for (int i = 0; i < n; i ++ ) cin >> g[i];

    sort(g, g + n);
    reverse(g, g + n);

    dfs1(0, 0);

    sort(w, w + cnt);
    cnt = unique(w, w + cnt) - w;
    reverse(w, w + cnt);

    dfs2(n / 2 + 2, 0);

    cout << res << endl;

    return 0;
}