筛法求欧拉函数

顾名思义就是在用线性筛求质数的过程中将每个数的欧拉函数求出，时间复杂度为O(n)；

欧拉函数：

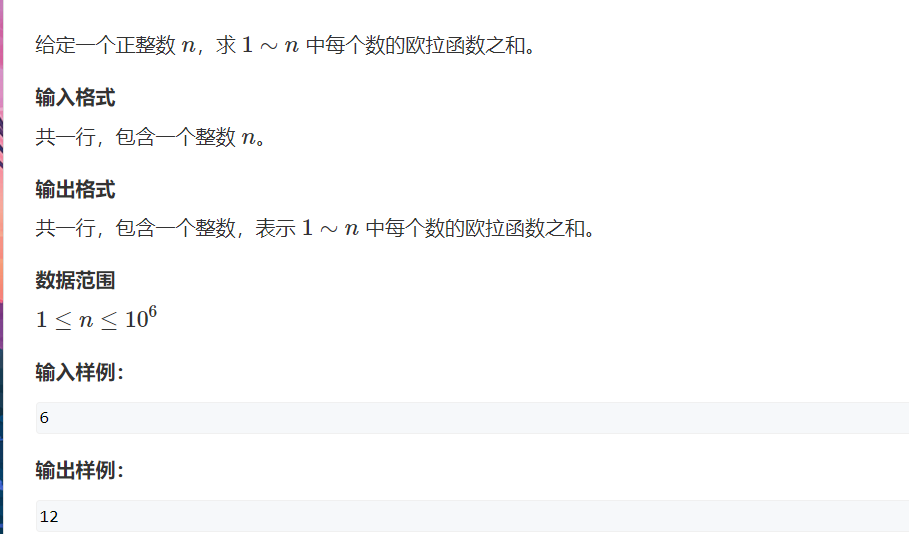
题目：

 

 

 思路：

求质数的过程中遇到了三种情况，分别是

 if (!st[i]) prime[cnt ++] = i;

if (i % prime[j] == 0) break;

st[prime[j] * i] = true;

接下来对三种情况分别进行分析：

第一种情况表示当前的数 i 为质数，而质数的欧拉函数为 i - 1，所以我们可以将代码改为：

if (!st[i]) 
{
     prime[cnt ++] = i;
     phi[i] = i - 1;
}

第二种情况表示 prime[j] 为 i 的一个质因子，那么如果 i 的欧拉函数为 i * (1 - 1 / p1) * (1 - 1 / p2) ……(1 - 1 / pk)，那么 prime[j] * i 的欧拉函数为 prime[j] * i * (1 - 1 / p1) * (1 - 1 / p2) ……(1 - 1 / pk)，所以代码可以改为：

st[prime[j] * i] = true;
phi[prime[j] * i] = phi[i] * (prime[j] - 1);

第三种情况表示当前是一个合数且最小质因子是 prime[j]，这种情况之下如果 i 的欧拉函数为 i * (1 - 1 / p1) * (1 - 1 / p2) ……(1 - 1 / pk)，则 prime[j] * i 的欧拉函数为 prime[j] * i * (1 - 1 / p1) * (1 - 1 / p2) ……(1 - 1 / pk) * (1 - 1 / prime[j])。所以代码可以改为：

if (i % prime[j] ==  0) 
{
    phi[prime[j] * i] = phi[i] * prime[j];
    break;
}

证毕。

总的代码如下：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1000010;

LL phi[N];
int prime[N];
bool st[N];
int n, cnt;

LL get_phi(int n)
{
    phi[1] = 1;
    for (int i = 2; i <= n; i ++ ) 
    {
        if (!st[i]) 
        {
            prime[cnt ++] = i;
            phi[i] = i - 1;
        }
        for (int j = 0; prime[j] <= n / i; j ++ ) 
        {
            st[prime[j] * i] = true;
            if (i % prime[j] ==  0) 
            {
                phi[prime[j] * i] = phi[i] * prime[j];
                break;
            }
            phi[prime[j] * i] = phi[i] * (prime[j] - 1);
        }
    }

    LL res = 0;
    for (int i = 1; i <= n; i ++ )
        res += phi[i];

    return res;
}

int main() 
{
    scanf("%d", &n);

    cout << get_phi(n) << endl;

    return 0;
}