bellman_ford算法

Bellman-Ford算法，对于一个有向图，可以分别求出图中所有点到一个确定点的最短距离。

基本思想就是枚举每一个点，判断通过该边能否使得其起点到原点的距离变短。

 

 

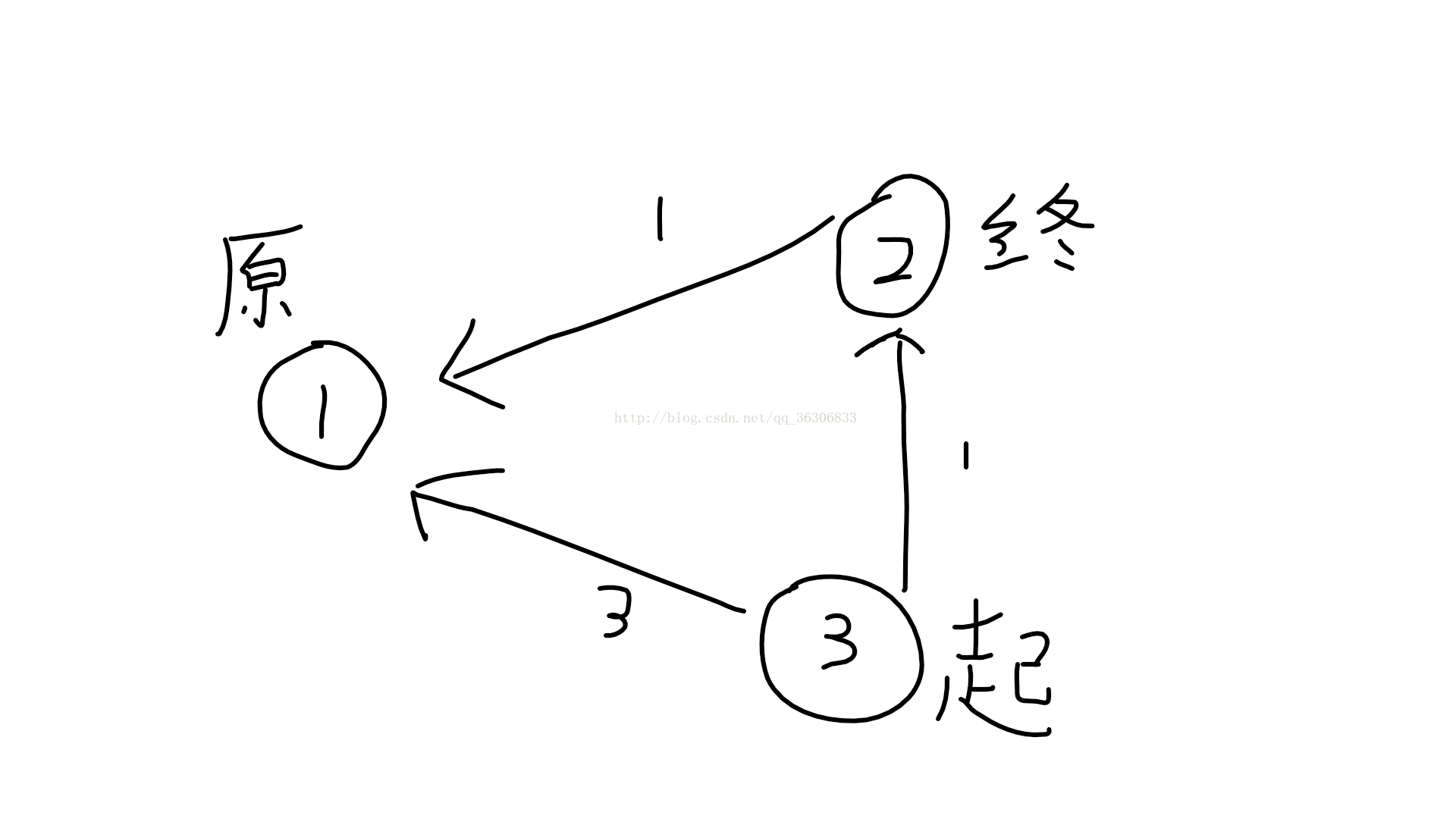
对于边3-2，它可以使3-1变成3-2-1，从而使其距离变短，此过程称为松弛。（松弛点数，拉紧距离）

 

边3-2可以松弛的条件：

1.边3-2存在。（对于核心代码来说，枚举所有边就已经保证了其存在，否则将不可能被枚举出来）

2.边2-1存在。（对于核心代码，实际实现的时候，2-1的距离设为的为Inf，即一个很大的数。）

3.边3-2权值+边2-1权值<边3-1权值。（判断语句实现）

---

 

题目

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从1号点到n号点的最多经过k条边的最短距离，如果无法从1号点走到n号点，输出impossible。

注意：图中可能 存在负权回路 。

输入格式

第一行包含三个整数n，m，k。

接下来m行，每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式

输出一个整数，表示从1号点到n号点的最多经过k条边的最短距离。

如果不存在满足条件的路径，则输出“impossible”。

数据范围

1≤n,k≤5001≤n,k≤500,
1≤m≤100001≤m≤10000,
任意边长的绝对值不超过10000。

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=505,M=100010;
int n,m,k;
int dist[N],backup[N];//dist存储初始节点到目标节点的距离，backup用于储存上一次的最短距离 
struct ford//定义一个结构体 
{
    int a,b,w;
}ford[M];
int bellman_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    for(int i=1;i<=k;i++)
    {
        memcpy(backup,dist,sizeof dist);//copy一遍距离 
        for(int j=1;j<=m;j++)
        {
            int a=ford[j].a,b=ford[j].b,w=ford[j].w;
            dist[b]=min(dist[b],backup[a]+w);//松弛操作 
        }
    }
    if(dist[n]>=0x3f3f3f3f/2) return 0;//由于你可能是在0x3f3f3f3f的基础上进行松弛操作，因此距离可能是小于0x3f3f3f3f的 
    else return dist[n];
}
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=m;i++)
    {
        int a,b,w;
        scanf("%d%d%d",&a,&b,&w);
        ford[i]={a,b,w};
    }
    int ans=bellman_ford();
    if(ans) printf("%d\n",ans);
    else puts("impossible");
    return 0; 
}

 

---

 

进行松弛操作的意义就是：避免你在限定了只能走n步的情况下走了n+m步。

原因：

3 3 1
1 2 1
2 3 1
1 3 3

　　这个样例，限定了你只能走1步，这样当你在第一步进行松弛操作时，如果你没有copy则你会将使用1->2松弛之后的距离1来进行下一步松弛，即使1->3的距离变成了1->2+2->3，这样就相当于你走了2步，而题目要求只能走1步；如果你进行了copy之后，你会将使用copy之后的无穷大来进行松弛2->3操作这时就不是最小值，也就是答案输出的是1->3松弛的3，这样就避免了你多走了1步。
　　推广到一般情况就是这个copy应该是避免你多走了几步，因为当你走到某一个点，并且更新了最小值时，copy一遍之后就是在上一次更大距离的情况下更新，这样得到的距离并不是最小的，这样当你下一次增加了一步之后就可以当前更小的距离来更新，否则你就会直接在当前最小的距离上更新，相当于多走了1步。