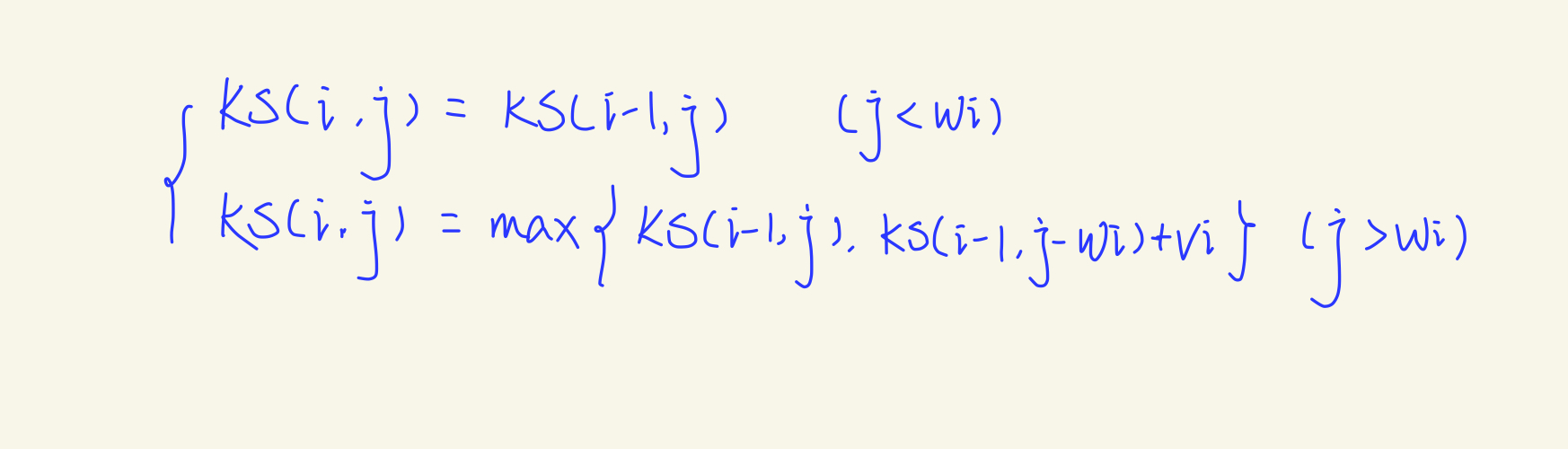01背包
上题目:
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 v[i],价值是 w[i]。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 v[i],w[i],用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤1000
0<vi,wi≤1000
01背包问题就是给你n个物品,你可以选择放入背包或者不放入背包,最后求在有限背包容积的情况下求出所装物品的最大价值。
代码:
1 #include<iostream> 2 using namespace std; 3 const int N=1010; 4 int w[N],v[N]; 5 int dp[N][N];//用dp数组来存储每一种状态 6 int main() 7 { 8 int n,m; 9 cin>>n>>m; 10 for(int i=1;i<=n;i++) 11 cin>>v[i]>>w[i];//重量和价值 12 for(int i=1;i<=n;i++) 13 { 14 for(int j=1;j<=m;j++) 15 { 16 if(j<v[i]) dp[i][j]=dp[i-1][j]; 17 else dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);//用递推来实现状态转移方程 18 //dp数组的每一行代表每一种物品,每一列代表改物品是否储存,以及储存之后的总价值 19 } 20 } 21 cout<<dp[n][m]; 22 return 0; 23 }
在这里,聪明的你应该能发现,其实这里大部分的内容都没有用上,那么让我们来想想,如何优化一下空间复杂度呢?
再回头看下之前的递推关系式:
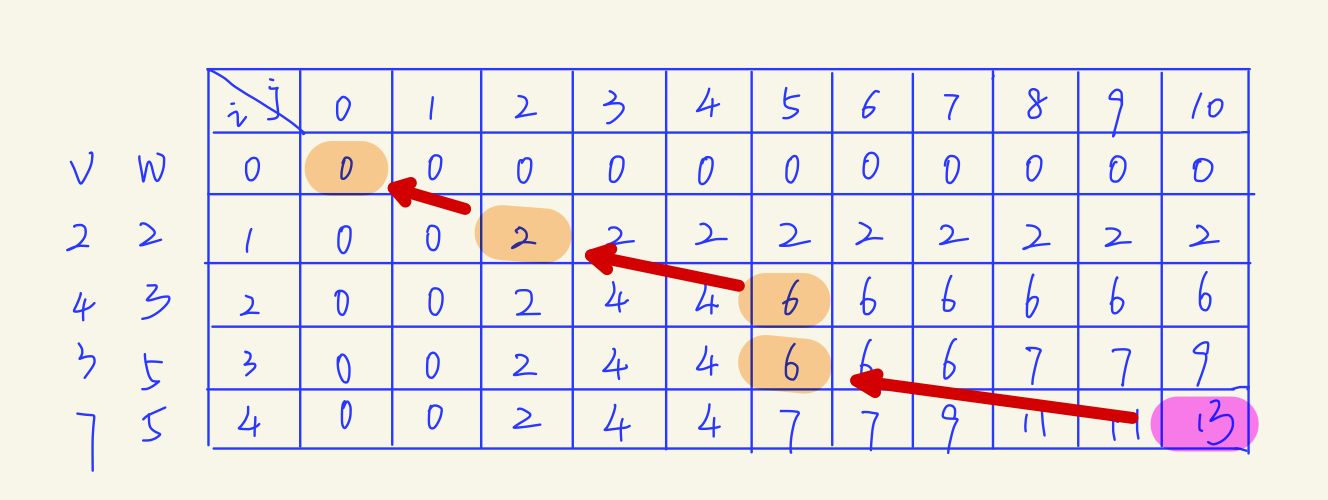
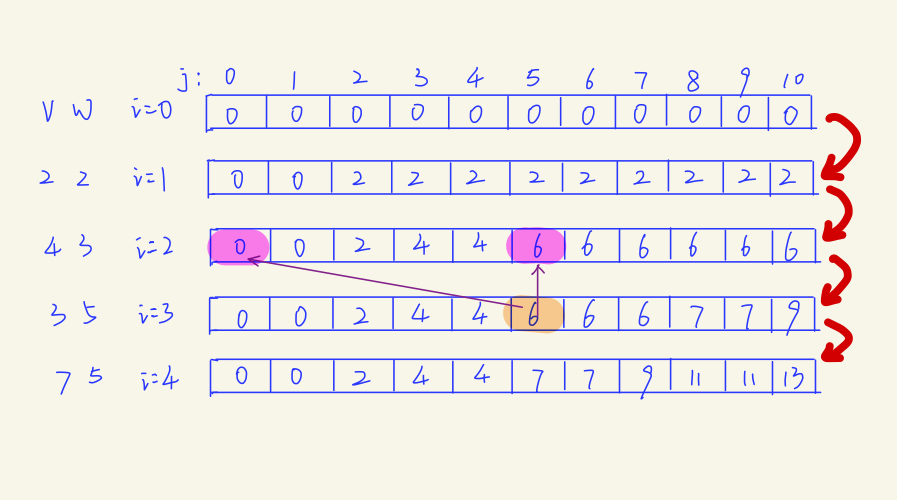
可以发现,每次求解 dp(i,j)只与dp(i-1,m) {m:1...j} 有关。也就是说,如果我们知道了dp(i-1,1...j)就肯定能求出dp(i,j),为了更直观的理解,再画一张图:
下一层只需要根据上一层的结果即可推出答案,举个栗子,看i=3,j=5时,在求这个子问题的最优解时,根据上述推导公式,dp(3,5) = max{dp(2,5),dp(2,0) + 3} = max{6,3} = 6;如果我们得到了i=2时所有子问题的解,那么就很容易求出i=3时所有子问题的解。
这时我们就可以用到滚动数组的思想。
那么我们就能优化为 dp[j]=max(dp[j],dp[j-v[i]]+w[i])。当然只有j大于v[i]时才有效。