朴素Dijkstra算法

Dijkstra算法

 

Dijkstra算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。

 

问题引入：

指定一个点（源点）到其余各个顶点的最短路径，也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。

 

 

 

 

 

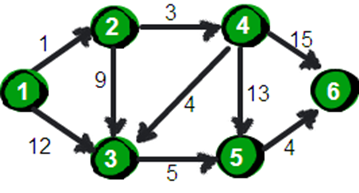
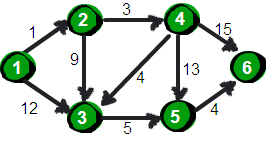
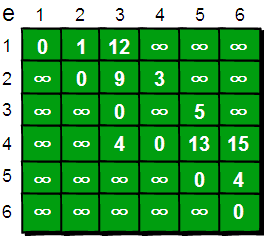
 下面我们来模拟一下：

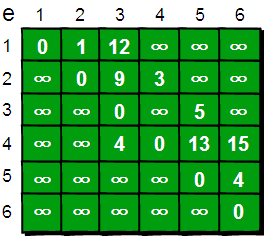
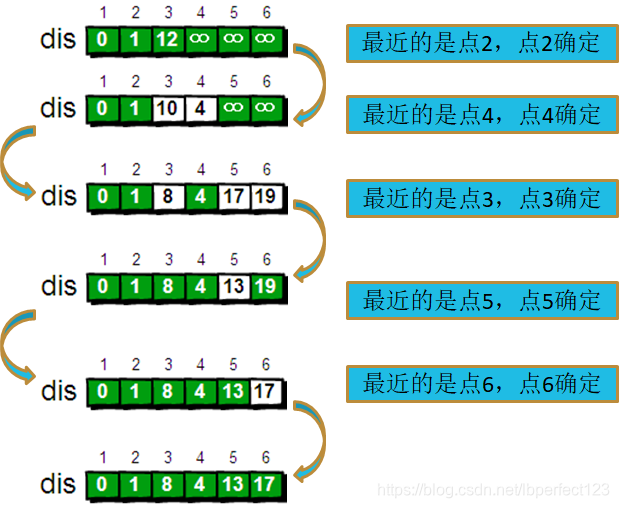
代码：

//邻接矩阵是用列模拟每一个点，每一行来表示每一列表示的点到每个点的距离
//如果能走到则距离为具体数字若不能走到则为无穷大即0x3f3f3f3f 
//朴素Dijkstra算法实质找到每个点到每个点的最短距离中的最小距离
//并且更新d[]，更新1号点到其他点的距离  
//再从这个最短距离的点去寻找其能寻找到的最短的距离 
#include<iostream>
#include<cstring>
#include<algorithm> 
using namespace std;
const int N=505;
int n,m;
int q[N][N],d[N];//q储存稠密图的邻接矩阵d储存1到每个点的最小距离 
bool st[N];//标记每个数是否被找到最短距离 
int dijkstra()
{
    d[1]=0;
    for(int i=1;i<=n;i++)//由于这里是从0开始遍历并且除了d[1]其他都是0x3f3f3f3f，所以第一次找到的最小距离的下标就是1，因此这样就可以把dist距离更新为1号点到其他点的距离
    {
        int t=-1;
        for(int j=1;j<=n;j++)//遍历一遍d 
        {
            if(!st[j]&&(t==-1||d[j]<d[t]))//如果没有找到最短距离并且t没有更新或者有更短的距离 
                t=j;
        }
        st[t]=true;
        for(int j=1;j<=n;j++)
            d[j]=min(d[j],d[t]+q[t][j]);//松弛操作 
            //此处为即为1->t->j 更新1到j的最短距离就用1到t的距离加上t到j的距离 
    }
    if(d[n]!=0x3f3f3f3f) return d[n];
    else return -1; 
}
int main()
{
    cin>>n>>m;
    memset(q,0x3f,sizeof q);//给每个数赋值为无穷大，无穷大的数值0x3f3f3f3f字节为0x3f 
    memset(d,0x3f,sizeof d);
    while(m--)
    {
        int a,b,c;
        cin>>a>>b>>c;
        q[a][b]=min(q[a][b],c);//可能有重边且权重不同 
    }
    cout<<dijkstra()<<endl;
    return 0;
 }