【洛谷】3960:列队【Splay】
题目描述
Sylvia 是一个热爱学习的女孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有n×m名学生,方阵的行数为 n,列数为 m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 n×m 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列 的学生的编号是(i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 q件这样的离队事件。每一次离队事件可以用数对(x,y)(1≤x≤n,1≤y≤m)描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
-
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 x 行第 m列。
-
向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 n 行第 m列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行 第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
输入输出格式
输入格式:
输入共 q+1 行。
第 1 行包含 3 个用空格分隔的正整数 n,m,q,表示方阵大小是 n 行 m 列,一共发 生了 q 次事件。
接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x,y,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 x 行第 y 列。
输出格式:
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学 生的编号。
输入输出样例
说明
【输入输出样例 1 说明】
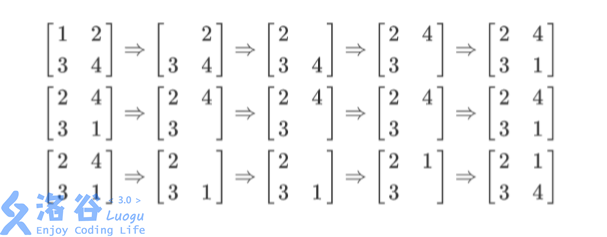
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为1 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 2的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为4的同学向上一步,这时空位移动到第二行第二列。最后编号 为1 的同学返回填补到空位中。
【数据规模与约定】
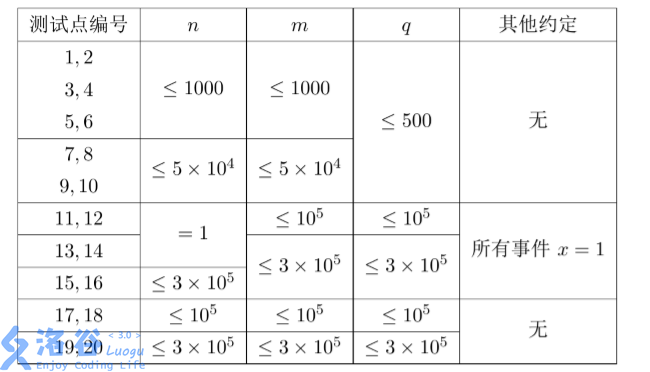
数据保证每一个事件满足 1≤x≤n,1≤y≤m
Solution
感天动地!!虽然觉得Splay这种东西学会了也没什么机会用,但是写对了吼开心!!!
做法其实就是模拟移动过程,每一排建一颗Splay,除了最后一列,最后一列单独建。
然后取出操作就变成了取出第$x$棵Splay的第$y$个($y=m$时取最后一列的第$x$个即可)。
空间限制使这种操作变成动态拆点,要拆所取点的大点时,就是把这个大点分成三块,前面,它本身,后面(很容易理解吧??QAQ)
取出第$k$个时顺便删除。然后把这个点push到最后一列的Splay末尾,再把最后一列的第$x$个弹出push到第$x$排的末尾就可以了。
最后一列其实不用特判,直接取出放到当前这排的最后位置也没有关系,反而这样方便取出答案。
然后注意的是每棵树root是单独存在的aaaaaaaa!!!
Code
#include<bits/stdc++.h> #define LL long long using namespace std; LL siz[3000005], l[3000005], r[3000005]; int tail, fa[3000005], son[3000005][2]; struct Splay { int root;////////每棵Splay的root是单独存在的!!!! int newnode(LL ll, LL rr) {///siz表示一段区间 ++ tail; fa[tail] = son[tail][0] = son[tail][1] = 0; siz[tail] = (r[tail] = rr) - (l[tail] = ll); return tail; } void init(LL ll, LL rr) { root = newnode(ll, rr); } void update(int nd) { siz[nd] = siz[son[nd][0]] + siz[son[nd][1]] + r[nd] - l[nd]; } void rotate(LL nd, int d) { int s = son[nd][!d]; int ss = son[s][d]; int f = fa[nd]; fa[s] = f; fa[nd] = s; if(ss) fa[ss] = nd; son[s][d] = nd; son[nd][!d] = ss; if(f) son[f][nd==son[f][1]] = s; else root = s; update(nd); update(s); } void splay(int nd, int top = 0) { while(fa[nd] != top) { int f = fa[nd]; int fl = nd == son[f][0]; int p = fa[f]; if(p == top) { rotate(f, fl); } else { int pl = f == son[p][0]; if(pl == fl) { rotate(p, pl); rotate(f, fl); } else { rotate(f, fl); rotate(p, pl); } } } } int splitnode(int nd, LL k) {//拆下前k个 k += l[nd]; int y = newnode(k, r[nd]);//拆下后面 同时返回拆出的这个点 r[nd] = k; if(son[nd][1] == 0) fa[son[nd][1] = y] = nd; else { int t = son[nd][1]; while(son[t][0]) t = son[t][0]; fa[son[t][0] = y] = t; while(t != nd) update(t), t = fa[t]; } splay(y); return y; } LL kth(LL k) { int nd = root; while(1) { if(siz[son[nd][0]] >= k) nd = son[nd][0]; else { k -= siz[son[nd][0]]; if(k <= r[nd] - l[nd]) { if(k != r[nd] - l[nd]) splitnode(nd, k);//去掉后面 if(k != 1) nd = splitnode(nd, k - 1);///就是当前需要的这个点 break; } else { k -= r[nd] - l[nd]; nd = son[nd][1]; } } } splay(nd); fa[son[nd][0]] = fa[son[nd][1]] = 0;///取出来并删除 if(!son[nd][0]) { root = son[nd][1]; } else { int t = son[nd][0]; while(son[t][1]) t = son[t][1]; splay(t); update(root = fa[son[t][1] = son[nd][1]] = t); } return l[nd]; } void pushback(LL k) {///放到最后 int t = newnode(k, k + 1); if(!root) root = t; else { int nd = root; while(son[nd][1]) nd = son[nd][1]; splay(nd); update(fa[son[nd][1] = t] = nd); } } } s[300005]; int main() { int n, m, q; scanf("%d%d%d", &n, &m, &q); for(LL i = 1; i <= n; i ++) s[i].init((i - 1) * m + 1, i * m); s[0].init(m, m + 1);///最后一列单独建树 for(LL i = 2; i <= n; i ++) s[0].pushback(i * m); int x, y; LL p; for(int i = 1; i <= q; i ++) { scanf("%d%d", &x, &y); s[x].pushback(s[0].kth(x)); printf("%lld\n", p = s[x].kth(y)); s[0].pushback(p); } return 0; }

