【11.2晚校内测试】【装桶模拟】【单调栈】

真的是fo了，晚上还来一次测试......

---

mister
【问题描述】 不久前 Mister 从太空中探测到一个奇怪的信号，他开始研究这个信号。 经过一些变换后，这个信号变成了长度为 n 的排列或者它的循环移位。对于进一步的研究 Mister 需要一些数据分析，这就是为什么他决定选择这个排列的循环移位，它有最小的可 能偏差。
我们把排列的偏差定义为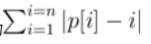

求一个可能偏差最小的排列 p 的循环移位。 让我们表示 k(0≤k < n)的循环移位排列 p 的变化需要达到这种转变,例如: k = 0: 变成 p1 p2 … pn, k = 1: 变成 pn p1 … pn - 1, …, k = n - 1: 变成 p2 p3 … pn p1。
【输入格式】 第一行包含单个整数 n(2≤n≤10^6)——排列的长度。 第二行包含 n 个空格分隔的整数 p1 p2 … pn(1≤pi≤n)的元素排列。 保证所有元素都是不同的。
【输出格式】 输出一个整数:排列 p 的循环移位的最小偏差。
【样例数据】 Input 3 2 3 1 Output 0 Input 3 3 2 1 Output 2
【数据范围】 10%的数据：n<=100 30%的数据：n<=2000 70%的数据：n<=50000 100%的数据：n<=1000000

---

 Solution

 一开始毫无头绪QAQ

发现规律，如果当前位置的值大于这个位置，那么每往后平移一步，答案会减少1，反之答案会增加1。以下把$p[i]-i$称为某一位的贡献，$p[i]-i>=0$称为贡献为正，反之称为贡献为负。

所以考虑怎么每次快速维护答案的增减量。如上诉，明显需要维护每平移一步贡献从正变成负和从负变成正的数的个数，开个桶可以$O(1)$处理出初始每个数需要多少步会改变符号，装到桶里表示经过$i$步有多少个数贡献会变负。

发现如果当前位置贡献为负，那么往后平移贡献会始终为负，除了最后一位跳到第一位可能会变化，进行特殊处理即可。

所以每次贡献为正的数量减去之前桶处理的，贡献为负的加上桶处理的，就是当前贡献为正和为负的数量。答案减去正的加上负的再更新最后一位的特判就是新的答案。

还有一些细节在代码中展示。

Code

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdio>
#define LL long long
using namespace std;

int p[2000005], cur[2000005];

int main() {
    int n;
    scanf("%d", &n);
    LL sum = 0, L = 0, R = 0, tmp = 0;
    for(int i = 1; i <= n; i ++) {
        scanf("%d", &p[i]);
        sum += abs(p[i] - i);
        if(p[i] >= i)    L ++, cur[p[i] - i] ++;
        else    R ++;
    }
    LL ans = sum;
    for(int i = 0; i < n - 1; i ++) {////i表示的是进行i+1次平移（方便下标写法 
        L -= cur[i];    R += cur[i];
        sum = sum - L + R - 1 - abs(p[n - i] - n) + p[n - i] - 1;//第n位贡献一定为负，所以要减去负的贡献中多算的一个 
        cur[p[n - i] + i] ++;//第一位贡献一定为正 
        L ++, R --;
        if(sum < ans)    ans = sum, tmp = i + 1;
    }
    printf("%lld %d\n", ans, tmp);
    return 0;
}

---

array
【问题描述】 给你一个由 n 个元素组成的数组。这个数组的某个连续子序列的不平衡值是这个段中最大 和最小元素的差值。数组的不平衡值是该数组所有连续子序列不平衡值的总和。 例如，数组[1,4,1]的失衡值为 9，因为这个数组有 6 个不同的子段: [1](从 a1 到 a1)，失衡值为 0; [1,4](从 a1 到 a2)，失衡值为 3; [1,4,1](从 a1 到 a3)，失衡值为 3; [4](从 a2 到 a2)，失衡值为 0; [4,1](从 a2 到 a3)，失衡值为 3; [1](从 a3 到 a3)，失衡值为 0; 你需要确定数组 a 的不平衡值。
【输入格式】 第一行包含一个整数 n(1≤n≤10^6)数组的长度。 第二行包含 n 个整数 a1 a2 … an (1≤ai≤10^6)——的元素数组。
【输出格式】 输出一个整数： a 数组的不平衡值。
【样例数据】 Input 3 1 4 1 Output 9
【数据范围】 10%的数据：n<=100 30%的数据：n<=5000 70%的数据：n<=10^5 100%的数据：n<=10^6

---

Solution

看起来好单调栈！！但是为什么仔细一想好不可做？？

实际上就是单调栈....

答案就等于$\sum{a[i]*(以a[i]为最大值的区间个数-以a[i]为最小值的区间个数}$QAQ，仔细想想是不是好有道理QAQAQAQ

Code

#include<bits/stdc++.h>
using namespace std;

inline int read() {
    int x = 0, t = 0; char ch = getchar();
    while(!isdigit(ch))    t |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
    return x *= (t ? -1 : 1);
}

int l[1000005], r[1000005], a[1000005], stk[1000005], top, n;
long long ans;
int main() {
    freopen("array.in", "r", stdin);
    freopen("array.out", "w", stdout);
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++)    a[i] = read();
    for(int i = 1; i <= n; i ++)    l[i] = r[i] = i;
    for(int i = 1; i <= n; i ++) {
        while(top && a[i] >= a[stk[top]]) {
            r[stk[top]] = i - 1;
            top --;
        }
        l[i] = stk[top] + 1;
        stk[++top] = i;
    }
    while(top) {
        r[stk[top]] = n;
        top --;
    }
    for(int i = 1; i <= n; i ++)    ans += 1ll * a[i] * (i - l[i] + 1) * (r[i] - i + 1);
    for(int i = 1; i <= n; i ++)    l[i] = r[i] = i;    top = 0;
    for(int i = 1; i <= n; i ++) {
        while(top && a[stk[top]] >= a[i]) {
            r[stk[top]] = i - 1;
            top --;
        }
        l[i] = stk[top] + 1;
        stk[++top] = i;
    }
    while(top) {
        r[stk[top]] = n;
        top --;
    }
    for(int i = 1; i <= n; i ++)    ans -= 1ll * a[i] * (i - l[i] + 1) * (r[i] - i + 1);
    printf("%lld", ans);
    return 0;
}