【10.24校内测试】【欧拉路径(有向+无向)】【双向链表/树状数组/线段树】


Solution
实际上是一道欧拉路径的裸题,不过以前完全没有写过,然后就很难受地挂掉了QAQ
分为有向图和无向图,如果有欧拉路径一定满足:
有向图:1、至多有两个点出度和入度不同,并且一定是一个出度=入度+1(起点),一个是入度=出度+1(终点)。2、如果所有点的出入度都应该相同,那么整个图就是一个环,起点可以任意定。
无向图:1、至多有两个奇点,且两个中一个是起点一个是终点。2、如果没有奇点,那么整个图就是一个环,起点任意定。
根据以上信息,要找出一条欧拉路径,就可以首先判断图中点的度数是否满足上述条件。
然后如何求路径?
确定起点后进行dfs,在回溯回去的过程中用栈保存路径,这样就能使栈顶到栈底储存的边是起点到终点的,输出就从栈顶输出到栈底即可。
Code
#include<bits/stdc++.h> using namespace std; inline void read(int &x) { x = 0; int t = 1; char ch = getchar(); while(ch > '9' || ch < '0') { if(ch == '-') t = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } x *= t; } struct Node { int v, nex, id; Node( ) { } Node(int v, int nex, int id) : v(v), nex(nex), id(id) { } } Edge[800005]; int stot = 1, h[800005]; void add(int u, int v, int id) { Edge[++stot] = Node(v, h[u], id); h[u] = stot; } int vis[800005], stk[800005], tp; void dfs(int u, int id) { for(int i = h[u]; i; i = Edge[i].nex) { if(vis[i]) continue; int v = Edge[i].v; vis[i] = vis[i ^ 1] = 1; dfs(v, i); } stk[++ tp] = Edge[id].id; } int d[800005], in[800005], out[800005], N, M; void work() { int st = 0x3f3f3f3f; for(int i = 1; i <= N; i ++) { int u, v; read(u), read(v); add(u, v, i); add(v, u, -i); d[u] ++; d[v] ++; st = min(st, min(u, v)); } int cnt = 0; for(int i = 1; i <= M; i ++) { if(d[i] & 1) cnt ++, st = i; } if(cnt > 2 || cnt == 1) { puts("NO"); return ; } dfs(st, 0); if(tp != N + 1) { puts("NO"); return ; } puts("YES"); for(int i = tp - 1; i; i --) printf("%d ", stk[i]); } void dfs2(int u, int id) { for(int i = h[u]; i; i = Edge[i].nex) { if(vis[i]) continue; int v = Edge[i].v; vis[i] = 1; dfs2(v, i); } stk[++ tp] = Edge[id].id; } void work2() { int st = 0, ed = 0; for(int i = 1; i <= N; i ++) { int u, v; read(u), read(v); add(u, v, i); in[v] ++; out[u] ++; } int cnt = 0; for(int i = 1; i <= M; i ++) { if(in[i] != out[i]) { cnt ++; if(in[i] == out[i] + 1) ed = i; if(out[i] == in[i] + 1) st = i; } } if((cnt != 0 && cnt != 2) || ((!st || !ed) && cnt)) { puts("NO"); return ; } if(!st) { for(int i = 1; i <= M; i ++) if(in[i] || out[i]) { st = i; break; } } dfs2(st, 0); if(tp != N + 1) { puts("NO"); return ; } puts("YES"); for(int i = tp - 1; i; i --) printf("%d ", stk[i]); } int main() { freopen("merge.in", "r", stdin); freopen("merge.out", "w", stdout); int T; scanf("%d%d%d", &T, &M, &N); if(T == 1) work(); else work2(); return 0; }

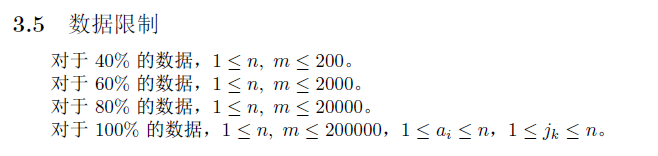
Solution
暴力60分很好得,每次暴力修改序列再重新用树状数组求逆序对即可,复杂度$mnlog_n$
实际上我们发现,每个位置的数的贡献在修改后是有规律的。贡献指的是以这个数开头的逆序对数。
给定j,将j后面所有小于等于j位置的数重新排序安插进去,此时这些数的贡献都会清零。因为在这些数后面并且比这些数小的数必定在修改后会变到这些数的前面,意味着以这些数开头的逆序对都不存在了。所以每次我们只用在上一次答案的基础上减去所有这些数的贡献即可。
但是对于其它无关的点难道不会有影响吗?先考虑j前面的点,这些点后面比他们小的数怎么都不可能跑到他们前面去,因此贡献不变。j后面比j位置大的数呢?虽然修改后数有变化,但是这些数的位置始终不变,比j位置还大的数一定比修改的这些数都大,所以可能逆序对会发生变化,逆序对数始终不变,他们的贡献也不变。
所以如何快速找出这些需要减去贡献的数呢?比较暴力的做法是双头链表(然而过绰绰有余),沿着链表查询,每次遇到这种需要修改的数就用链表把前后连在一起,把这个位置删掉,贡献清零。很玄学但是非常好写!简直就是在暴力上加两行代码就可以了。
还有一种是用线段树,每次在j到n的区间查询最小值修改,直到最小值比j位置大。这样做均摊复杂度比较优,因为每个点只会被修改一次,近似$nlog_n$
然而我还是写的链表,还是贴一波$jz$dalao的线段树八~
Code
链表
#include<bits/stdc++.h> #define LL long long #define RG register using namespace std; inline void read(int &x) { x = 0; int t = 1; char ch = getchar(); while(ch > '9' || ch < '0') { if(ch == '-') t = -1; ch = getchar(); } while(ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } x *= t; } int n, m; int a[200005]; int lowbit(int x) { return x & -x; } LL las[200006]; void insert(int pos, int d) { for(RG int i = pos; i <= n; i += lowbit(i)) las[i] += d; } LL query(int pos) { int ans = 0; for(RG int i = pos; i; i -= lowbit(i)) ans += las[i]; return ans; } LL gx[200005]; int nex[200005], pre[200005]; int main() { freopen("count.in", "r", stdin); freopen("count.out", "w", stdout); scanf("%d%d", &n, &m); LL res = 0; for(int i = 1; i <= n; i ++) read(a[i]); for(int i = n; i >= 1; i --) { gx[i] = query(a[i] - 1); res += gx[i]; insert(a[i], 1); } printf("%lld ", res); for(int i = 1; i <= n; i ++) nex[i] = i + 1, pre[i] = i - 1; for(RG int i = 1; i <= m; i ++) { int j; read(j); if(!gx[j]) { printf("%lld ", res); continue; } for(RG int k = j; k <= n; k = nex[k]) if(a[k] <= a[j]) nex[pre[k]] = nex[k], pre[nex[k]] = pre[k], res -= gx[k], gx[k] = 0; printf("%lld ", res); } return 0; }
线段树
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #define ll long long using namespace std; const ll maxn = 2e5 + 5; ll n, m, ans = 0; ll read() { ll rt = 0, f = 1; char ch = getchar(); while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); } while (ch >= '0' && ch <= '9') { rt = (rt << 1) + (rt << 3) + ch - '0'; ch = getchar(); } return rt * f; } struct Tree { ll vmin, pos; }t[maxn << 2]; ll a[maxn], j[maxn], f[maxn], cnt[maxn], p[maxn], v[maxn], num; ll lowbit(ll x) { return x & (-x); } ll query(ll pos) { ll rt = 0; for (int i = pos; i >= 1; i-= lowbit(i)) { rt += f[i]; } return rt; } void modify(ll pos, ll val) { for (int i = pos; i <= n; i += lowbit(i)) { f[i] += val; } } void update(ll o) { if (t[o << 1].vmin < t[o << 1 | 1].vmin) { t[o] = t[o << 1]; } else { t[o] = t[o << 1 | 1]; } } void build(ll o, ll lf, ll rg) { if (lf == rg) { t[o].pos = lf; t[o].vmin = a[lf]; return ; } ll mid = (lf + rg) >> 1; build(o << 1, lf, mid); build(o << 1 | 1, mid + 1, rg); update(o); } void modify(ll o, ll lf, ll rg, ll pos, ll val) { if (lf == rg) { t[o].vmin = val; return ; } ll mid = (lf + rg) >> 1; if (pos <= mid) { modify(o << 1, lf, mid, pos, val); } else { modify(o << 1 | 1, mid + 1, rg, pos, val); } update(o); } Tree query(ll o, ll lf, ll rg, const ll L, const ll R) { if (L <= lf && rg <= R) { return t[o]; } ll mid = (lf + rg) >> 1; Tree rt1, rt2; bool flag1 = 0, flag2 = 0; if (L <= mid) { flag1 = 1; rt1 = query(o << 1, lf, mid, L, R); } if (R > mid) { flag2 = 1; rt2 = query(o << 1 | 1, mid + 1, rg, L, R); } if (flag1 && flag2) { if (rt1.vmin < rt2.vmin) return rt1; else return rt2; } else if (flag1 && !flag2) { return rt1; } else if (!flag1 && flag2) { return rt2; } } int main() { freopen("count.in","r",stdin); freopen("count.out","w",stdout); n = read(), m = read(); for (int i = 1; i <= n; i++) { a[i] = read(); } for (int i = 1; i <= m; i++) { j[i] = read(); } for (int i = n; i >= 1; i--) { ll now = query(a[i] - 1); cnt[i] = now; ans += cnt[i]; modify(a[i], 1); } build(1, 1, n); printf("%lld ",ans); for (int i = 1; i <= m; i++) { num = 0; while (1) { Tree now = query(1, 1, n, j[i], n); if (now.vmin > a[j[i]]) break; num += cnt[now.pos]; cnt[now.pos] = 0; modify(1, 1, n, now.pos, 1e9); } ans -= num; printf("%lld", ans); if (i != m) { printf(" "); } } return 0; }


