【洛谷】2144：[FJOI2007]轮状病毒【高精度】【数学推导？？（找规律）】

P2144 [FJOI2007]轮状病毒

题目描述

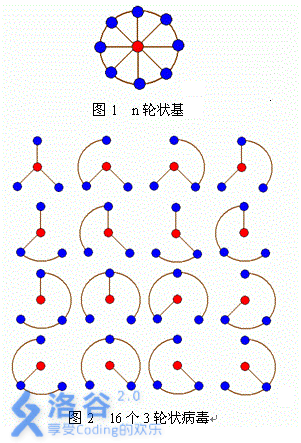
轮状病毒有很多变种。许多轮状病毒都是由一个轮状基产生。一个n轮状基由圆环上n个不同的基原子和圆心的一个核原子构成。2个原子之间的边表示这2个原子之间的信息通道，如图1。

n轮状病毒的产生规律是在n轮状基中删除若干边，使各原子之间有唯一一条信息通道。例如，共有16个不同的3轮状病毒，入图2所示。

给定n(N<=100)，编程计算有多少个不同的n轮状病毒。

输入输出格式

输入格式：

 

第一行有1个正整数n。

 

输出格式：

 

将编程计算出的不同的n轮状病毒数输出

 

输入输出样例

输入样例#1： 复制

3

输出样例#1： 复制

16

 

---

 

Solution

然而正解是一系列看都看不懂的公式推导.....

可能老李给我们这道题是为了复习一下高精度八.....

于是他的目的达到了，大家果然都忘记叻！

那么首先打表找规律，打表程序见某位dalao，用并查集实现的超级暴力。

然后找规律，目前了解到有两种规律：1）以1、3开头的斐波拉契数列的平方，如果$n$是偶数减4，奇数不减。2）$f[i]=3f[i-1]-f[i-2]+2$

个人认为第一种比较好找，所以用的第一种。因为斐波拉契数列到后面非常大，所以写高精。

这里用了高精加、乘、减，乱搞搞就过了。

Code

#include<bits/stdc++.h>
using namespace std;

int n;

struct Node {
    int a[105], len;
};

Node mul(Node a, Node b) {
    Node c;
    memset(c.a, 0, sizeof(c.a));
    for(int i = 1; i <= a.len; i ++) {
        int x = 0;
        for(int j = 1; j <= b.len; j ++) {
            c.a[i + j - 1] = a.a[i] * b.a[j] + x + c.a[i + j - 1];
            x = c.a[i + j - 1] / 10;
            c.a[i + j - 1] %= 10;
        }
        c.a[i + b.len] = x;
    }
    c.len = a.len + b.len;
    while(c.a[c.len] == 0 && c.len > 1)    c.len --;
    return c;    
}

Node add(Node a, Node b) {
    Node c;
    memset(c.a, 0, sizeof(c.a));
    for(int i = 1; i <= max(a.len, b.len); i ++) {
        int x = 0;
        c.a[i] = b.a[i] + a.a[i] + c.a[i];
        x = c.a[i] / 10;
        c.a[i] %= 10;
        c.a[i + 1] += x;
    }
    c.len = max(a.len, b.len) + 1;
    while(c.a[c.len] == 0 && c.len > 1) c.len --;
    return c;
}

Node sub(Node a, int x) {
    Node c;
    c.len = max(a.len, 1);
    c.a[1] = a.a[1] - 4;
    for(int i = 2; i <= c.len; i ++)    c.a[i] = a.a[i];
    for(int i = 1; i <= c.len; i ++) {
        if(c.a[i] < 0) {
            c.a[i + 1] --;
            c.a[i] = (c.a[i] + 10) % 10;
        }
    }
    while(c.a[a.len] == 0 && c.len > 1)    c.len --;
    return c;
}

void work() {
    Node a, b, c;
    memset(a.a, 0, sizeof(a.a));
    memset(b.a, 0, sizeof(b.a)); 
    a.len = b.len = 1;
    a.a[1] = 1, b.a[1] = 3;
    for(int i = 3; i <= n; i ++) {
        c = add(a, b);
        swap(a, b); swap(b, c);
    }
    c = mul(b, b);
    if(n % 2 == 0)
        c = sub(c, 4);
    for(int i = c.len; i >= 1; i --)
        printf("%d", c.a[i]);
}

int main() {
    scanf("%d", &n);
    if(n >= 3)    work();
    if(n == 1)    printf("1");
    if(n == 2)    printf("5");
    return 0;
}