【10.9校内练习赛】【搜索】【2-sat】【树链剖分】【A_star k短路】【差分约束+判负环】
在洛谷上复制的题目!
题目描述
n队伍比赛,每两支队伍比赛一次,平1胜3负0.
给出队伍的最终得分,求多少种可能的分数表。
输入输出格式
输入格式:
第一行包含一个正整数n,队伍的个数。第二行包含n个非负整数,即每支队伍的得分。
输出格式:
输出仅一行,即可能的分数表数目。保证至少存在一个可能的分数表。
输入输出样例
说明
N<=8
就是一个很暴力的搜索,然而在$vjudge$上能过洛谷怎么剪枝都过不了。
剪枝就是如果剩下的比赛全都胜都无法满足当前枚举的比赛双方人的分数,剪掉。
emmm...然后就没什么了,暴力搜就好了。(但是洛谷上过不了aaa!!只能水水$vjudge$叻)
#include<bits/stdc++.h> using namespace std; int n, a[10]; int now[20], ans, tot; struct Node { int x, y; Node(int x = 0, int y = 0) : x(x), y(y) { } } m[105]; inline void Swap(int &a, int &b) { int t = a; a = b; b = t; } int las[105]; void dfs(int dep) { if(dep == tot + 1) { for(int i = 1; i <= n; i ++) if(a[i] != now[i]) return ; ans ++; return ; } int x = m[dep].x, y = m[dep].y; if(now[x] + 3 * (las[x] - dep + 1) < a[x]) return ; if(now[y] + 3 * (las[y] - dep + 1) < a[y]) return ; for(int i = 0; i <= 1; i ++) { if(i == 1) Swap(x, y); if(dep == las[x]) { if(now[x] + 3 == a[x]) { now[x] += 3; dfs(dep + 1); now[x] -= 3; } if(now[x] + 1 == a[x]) { now[x] ++; now[y] ++; if(now[y] <= a[y]) dfs(dep + 1); now[x] --; now[y] --; } if(now[x] == a[x]) { now[y] += 3; if(now[y] <= a[y]) dfs(dep + 1); now[y] -= 3; } return ; } } if(now[x] + 3 <= a[x]) { now[x] += 3; dfs(dep + 1); now[x] -= 3; } if(now[x] + 1 <= a[x] && now[y] + 1 <= a[y]) { now[x] ++; now[y] ++; dfs(dep + 1); now[x] --; now[y] --; } if(now[y] + 3 <= a[y]) { now[y] += 3; dfs(dep + 1); now[y] -= 3; } } int main() { scanf("%d", &n); for(int i = 1; i <= n; i ++) scanf("%d", &a[i]); for(int i = 1; i <= n; i ++) { for(int j = i + 1; j <= n; j ++) m[++tot] = Node(i, j); las[i] = tot; } dfs(1); printf("%d", ans); return 0; }
题目描述
满汉全席是中国最丰盛的宴客菜肴,有许多种不同的材料透过满族或是汉族的料理方式,呈现在數量繁多的菜色之中。由于菜色众多而繁杂,只有极少數博学多闻技艺高超的厨师能够做出满汉全席,而能够烹饪出经过专家认证的满汉全席,也是中国厨师最大的荣誉之一。世界满汉全席协会是由能够料理满汉全席的专家厨师们所组成,而他们之间还细分为许多不同等级的厨师。
为了招收新进的厨师进入世界满汉全席协会,将于近日举办满汉全席大赛,协会派遣许多会员当作评审员,为的就是要在參赛的厨师之中,找到满汉料理界的明日之星。
大会的规则如下:每位參赛的选手可以得到n 种材料,选手可以自由选择用满式或是汉式料理将材料当成菜肴。
大会的评审制度是:共有m 位评审员分别把关。每一位评审员对于满汉全席有各自独特的見解,但基本见解是,要有兩样菜色作为满汉全席的标志。如某评审认为,如果没有汉式东坡肉跟满式的涮羊肉锅,就不能算是满汉全席。但避免过于有主見的审核,大会规定一个评审员除非是在认为必备的两样菜色都没有做出來的狀况下,才能淘汰一位选手,否则不能淘汰一位參赛者。
换句话說,只要參赛者能在这兩种材料的做法中,其中一个符合评审的喜好即可通过该评审的审查。如材料有猪肉,羊肉和牛肉时,有四位评审员的喜好如下表:
评审一 评审二 评审三 评审四
满式牛肉 满式猪肉 汉式牛肉 汉式牛肉
汉式猪肉 满式羊肉 汉式猪肉 满式羊肉 如參赛者甲做出满式猪肉,满式羊肉和满式牛肉料理,他将无法满足评审三的要求,无法通过评审。而參赛者乙做出汉式猪肉,满式羊肉和满式牛肉料理,就可以满足所有评审的要求。
但大会后來发现,在这样的制度下如果材料选择跟派出的评审员没有特别安排好的话,所有的參赛者最多只能通过部分评审员的审查而不是全部,所以可能会发生没有人通过考核的情形。
如有四个评审员喜好如下表时,则不论参赛者采取什么样的做法,都不可能通过所有评审的考核:
评审一 评审二 评审三 评审四
满式羊肉 满式猪肉 汉式羊肉 汉式羊肉
汉式猪肉 满式羊肉 汉式猪肉 满式猪肉 所以大会希望有人能写一个程序來判断,所选出的m 位评审,会不会发生 没有人能通过考核的窘境,以便协会组织合适的评审团。
输入输出格式
输入格式:
第一行包含一个数字 K,代表测试文件包含了K 组资料。
每一组测试资料的第一行包含兩个数字n 跟m(n≤100,m≤1000),代表有n 种材料,m 位评审员。
为方便起見,材料舍弃中文名称而给予编号,编号分别从1 到n。
接下來的m 行,每行都代表对应的评审员所拥有的兩个喜好,每个喜好由一个英文字母跟一个数字代表,如m1 代表这个评审喜欢第1 个材料透过满式料理做出來的菜,而h2 代表这个评审员喜欢第2 个材料透过汉式料理做出來的菜。
每个测试文件不会有超过50 组测试资料
输出格式:
每笔测试资料输出一行,如果不会发生没有人能通过考核的窘境,输出GOOD;否则输出BAD(大写字母)。
输入输出样例
2 3 4 m3 h1 m1 m2 h1 h3 h3 m2 2 4 h1 m2 m2 m1 h1 h2 m1 h2
GOOD BAD
给出题人点赞!!题目简直太无微不至叻!!于是乎一看就知道是$2-sat$的板子题叻!
把每种材料拆成两个点代表$h$和$m$两种食物,对于每一对评委,其中一种材料的相反食物连向另一种食物。表示如果不选这种食物就必须选另一种。
$tarjan$缩点,如果一个材料的两种食物在同一强联通分量,那么就输出$BAD$,其他就输出$GOOD$
#include<bits/stdc++.h> using namespace std; char s1, s2; void read(int &x) { x = 0; char ch = getchar(); while(ch > '9' || ch < '0') ch = getchar(); while(ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } } struct Node { int v, nex; Node(int v = 0, int nex = 0) : v(v), nex(nex) { } } Edge[100001]; int h[10001], stot; void add(int u, int v) { Edge[++stot] = Node(v, h[u]); h[u] = stot; } int dfn[205], low[205], ti, color[205], stk[205], cnt, tp; void tarjan(int u) { dfn[u] = low[u] = ++ ti; stk[++tp] = u; for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; if(!dfn[v]) { tarjan(v); low[u] = min(low[v], low[u]); } else if(!color[v]) low[u] = min(low[u], dfn[v]); } if(dfn[u] == low[u]) { cnt ++; int x; do { x = stk[tp--]; color[x] = cnt; } while(x != u); } } int main() { int T; scanf("%d", &T); while(T --) { memset(h, 0, sizeof(h)); memset(stk, 0, sizeof(stk)); memset(dfn, 0, sizeof(dfn)); memset(low, 0, sizeof(low)); memset(color, 0, sizeof(color)); cnt = 0, ti = 0, tp = 0; stot = 0; int flag = 0, n, m; scanf("%d%d", &n, &m); for(int i = 1; i <= m; i ++) { scanf("\n"); int a, b; s1 = getchar(); read(a); scanf(" "); s2 = getchar(); read(b); if(s1 == 'h') { if(s2 == 'h') { add(a + n, b); add(b + n, a); } else { add(a + n, b + n); add(b, a); } } else { if(s2 == 'h') { add(a, b); add(b + n, a + n); } else { add(a, b + n); add(b, a + n); } } } for(int i = 1; i <= n * 2; i ++) if(!dfn[i]) tarjan(i); for(int i = 1; i <= n; i ++) if(color[i] == color[i+n]) flag = 1; if(flag) printf("BAD\n"); else printf("GOOD\n"); } return 0; }
题目描述
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,⋯,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
输入输出格式
输入格式:
从文件manager.in中读入数据。
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式:
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
输入输出样例
7 0 0 0 1 1 5 5 install 5 install 6 uninstall 1 install 4 uninstall 0
3 1 3 2 3
10 0 1 2 1 3 0 0 3 2 10 install 0 install 3 uninstall 2 install 7 install 5 install 9 uninstall 9 install 4 install 1 install 9
1 3 2 1 3 1 1 1 0 1
说明
【样例说明 1】
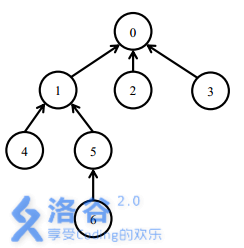
一开始所有的软件包都处于未安装状态。
安装5号软件包,需要安装0,1,5三个软件包。
之后安装6号软件包,只需要安装6号软件包。此时安装了0,1,5,6四个软件包。
卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。
之后安装4号软件包,需要安装1,4两个软件包。此时0,1,4处在安装状态。最后,卸载0号软件包会卸载所有的软件包。`
【数据范围】
【时限1s,内存512M】
实际上是一个披着紫题外衣的水体叻...相当于链剖的模板题叻!
我是把所有点没有安装赋值为1,要安装就是要把这个点到根节点全都安装,统计有多少1即可,并且把这条链修改为0.(沿着链向上走!!)
要卸载就是把这个点的子树全都卸载,直接保存$dfs$序,是一个区间,直接修改即可。
注意线段数中$tag$要订成-1,因为0表示一种状态。
#include<bits/stdc++.h> #define RG register using namespace std; int n, a[10]; void read(int &x) { x = 0; char ch = getchar(); while(ch > '9' || ch < '0') ch = getchar(); while(ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); } } struct Node { int v, nex; Node(int v = 0, int nex = 0) : v(v), nex(nex) { } } Edge[200001]; int h[100001], stot; void add(int u, int v) { Edge[++stot] = Node(v, h[u]); h[u] = stot; } int siz[100005], fa[100005], son[100005]; void dfs1(int u, int f) { siz[u] = 1; fa[u] = f; for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; if(v == f) continue; dfs1(v, u); siz[u] += siz[v]; if(siz[son[u]] < siz[v]) son[u] = v; } } int top[100005], in[100005], out[100005], ti; void dfs2(int u, int t) { top[u] = t; in[u] = ++ ti; if(son[u]) dfs2(son[u], t); for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; if(v == fa[u] || v == son[u]) continue; dfs2(v, v); } out[u] = ti; } int TR[400004], tag[400005]; inline void update(int nd) { TR[nd] = TR[nd << 1] + TR[nd << 1 | 1]; } void build(int nd, int l, int r) { tag[nd] = -1; if(l == r) { TR[nd] = 1; return ; } int mid = (l + r) >> 1; build(nd << 1, l, mid); build(nd << 1 | 1, mid + 1, r); update(nd); } inline void push_down(int nd, int l, int r) { if(tag[nd] != -1) { int mid = (l + r) >> 1; TR[nd << 1] = tag[nd] * (mid - l + 1); TR[nd << 1 | 1] = tag[nd] * (r - mid); tag[nd << 1] = tag[nd]; tag[nd << 1 | 1] = tag[nd]; tag[nd] = -1; } } int query(int nd, int l, int r, int L, int R) { if(l >= L && r <= R) return TR[nd]; push_down(nd, l, r); int mid = (l + r) >> 1; int ans = 0; if(L <= mid) ans += query(nd << 1, l, mid, L, R); if(R > mid) ans += query(nd << 1 | 1, mid + 1, r, L, R); return ans; } void modify(int nd, int l, int r, int L, int R, int d) { if(l >= L && r <= R) { TR[nd] = d * (r - l + 1); tag[nd] = d; return ; } push_down(nd, l, r); int mid = (l + r) >> 1; if(L <= mid) modify(nd << 1, l, mid, L, R, d); if(R > mid) modify(nd << 1 | 1, mid + 1, r, L, R, d); update(nd); } int query(int u) { int ans = 0; while(top[u] != 1) { ans += query(1, 1, n, in[top[u]], in[u]); u = fa[top[u]]; } ans += query(1, 1, n, in[1], in[u]); return ans; } void modify(int u) { while(top[u] != 1) { modify(1, 1, n, in[top[u]], in[u], 0); u = fa[top[u]]; } modify(1, 1, n, in[1], in[u], 0); } int main() { scanf("%d", &n); for(int i = 1; i < n; i ++) { int a; read(a); a ++; add(i + 1, a); add(a, i + 1); } dfs1(1, 1); dfs2(1, 1); build(1, 1, n); int q; scanf("%d", &q); for(RG int i = 1; i <= q; i ++) { char s[20]; int x; scanf("%s", s); scanf("%d", &x); x ++; if(s[0] == 'i') { printf("%d\n", query(x)); modify(x); } else { printf("%d\n", siz[x] - query(1, 1, n, in[x], out[x])); modify(1, 1, n, in[x], out[x], 1); } } return 0; }
题目描述
iPig在假期来到了传说中的魔法猪学院,开始为期两个月的魔法猪训练。经过了一周理论知识和一周基本魔法的学习之后,iPig对猪世界的世界本原有了很多的了解:众所周知,世界是由元素构成的;元素与元素之间可以互相转换;能量守恒……。
能量守恒……iPig 今天就在进行一个麻烦的测验。iPig 在之前的学习中已经知道了很多种元素,并学会了可以转化这些元素的魔法,每种魔法需要消耗 iPig 一定的能量。作为 PKU 的顶尖学猪,让 iPig 用最少的能量完成从一种元素转换到另一种元素……等等,iPig 的魔法导猪可没这么笨!这一次,他给 iPig 带来了很多 1 号元素的样本,要求 iPig 使用学习过的魔法将它们一个个转化为 N 号元素,为了增加难度,要求每份样本的转换过程都不相同。这个看似困难的任务实际上对 iPig 并没有挑战性,因为,他有坚实的后盾……现在的你呀!
注意,两个元素之间的转化可能有多种魔法,转化是单向的。转化的过程中,可以转化到一个元素(包括开始元素)多次,但是一但转化到目标元素,则一份样本的转化过程结束。iPig 的总能量是有限的,所以最多能够转换的样本数一定是一个有限数。具体请参看样例。
输入输出格式
输入格式:
第一行三个数 N、M、E 表示iPig知道的元素个数(元素从 1 到 N 编号)、iPig已经学会的魔法个数和iPig的总能量。
后跟 M 行每行三个数 si、ti、ei 表示 iPig 知道一种魔法,消耗 ei 的能量将元素 si 变换到元素 ti 。
输出格式:
一行一个数,表示最多可以完成的方式数。输入数据保证至少可以完成一种方式。
输入输出样例
说明
有意义的转换方式共4种:
1->4,消耗能量 1.5
1->2->1->4,消耗能量 4.5
1->3->4,消耗能量 4.5
1->2->3->4,消耗能量 4.5
显然最多只能完成其中的3种转换方式(选第一种方式,后三种方式仍选两个),即最多可以转换3份样本。
如果将 E=14.9 改为 E=15,则可以完成以上全部方式,答案变为 4。
数据规模
占总分不小于 10% 的数据满足 N≤6,M≤15。
占总分不小于 20% 的数据满足 N≤100,M≤300,E≤100且E和所有的ei均为整数(可以直接作为整型数字读入)。
所有数据满足2≤N≤5000,1≤M≤200000,1≤E≤107,1≤ei≤E,E和所有的ei为实数。
在洛谷上是卡A*的,然而$vjudge$上跑的飞快。估计老李就是把它当成模板题给我们做的吧....
作为一个日常最短路动不动就想写A*的蒟蒻,这个题解就不写叻,这次写用了一下$Dijistra$堆优化,感觉非常美妙,但是$stl$常数大,一般情况下慎用丫~
#include<bits/stdc++.h> using namespace std; int n, m; double e; struct Node { int v, nex; double w; Node(int v = 0, int nex = 0, double w = 0) : v(v), nex(nex), w(w) { } } Edge[200001], Edge_r[200005]; int h[5001], stot, h_r[5001], stot_r; void add(int u, int v, double w) { Edge[++stot] = Node(v, h[u], w); h[u] = stot; Edge_r[++stot_r] = Node(u, h_r[v], w); h_r[v] = stot_r; } struct Ed { int u; double dis; Ed(int u = 0, double dis = 0) : u(u), dis(dis) { } bool operator < (const Ed a) const { return dis > a.dis; } }; double dis[5001]; int flag[5001]; void Dijistra(int s) { priority_queue < Ed > q; for(int i = 1; i <= n; i ++) dis[i] = 0x3f3f3f3f; dis[s] = 0; q.push(Ed(s, 0)); while(!q.empty()) { Ed x = q.top(); int u = x.u; q.pop(); if(flag[u]) continue; flag[u] = 1; for(int i = h_r[u]; i; i = Edge_r[i].nex) { int v = Edge_r[i].v; if(dis[v] > dis[u] + Edge_r[i].w && !flag[v]) { dis[v] = dis[u] + Edge_r[i].w; q.push(Ed(v, dis[v])); } } } } struct A { int u; double h; A(int u = 0, double h = 0) : u(u), h(h) { } bool operator < (const A a) const { return h + dis[u] > a.h + dis[a.u]; } }; int cnt[5001], ans; void A_star() { int MA = 1.0 * e / dis[1]; priority_queue < A > q; q.push(A(1, 0)); while(!q.empty()) { A x = q.top(); q.pop(); int u = x.u; double he = x.h; if(he > e) return ; if(cnt[u] > MA) continue; cnt[u] ++; if(u == n) { e -= he; ans ++; continue; } for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; q.push(A(v, he + Edge[i].w)); } } } int main() { scanf("%d%d%lf", &n, &m, &e); for(int i = 1; i <= m; i ++) { int a, b; double c; scanf("%d%d%lf", &a, &b, &c); add(a, b, c); } if(e == 10000000) { printf("2002000"); return 0; } Dijistra(n); A_star(); printf("%d", ans); return 0; }
hdu 3666:THE MATRIX PROBLEM
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 9337 Accepted Submission(s):
2395
Each case includes two parts, in part 1, there are four integers in one line, N,M,L,U, indicating the matrix has N rows and M columns, L is the lowerbound and U is the upperbound (1<=N、M<=400,1<=L<=U<=10000). In part 2, there are N lines, each line includes M integers, and they are the elements of the matrix.
查分约束(近乎模板题)
#include<bits/stdc++.h> using namespace std; int n, m; double L, U; struct Node { int v, nex; double w; Node(int v = 0, int nex = 0, double w = 0) : v(v), nex(nex), w(w) { } } Edge[400001]; int h[200005], stot; void add(int u, int v, double w) { Edge[++stot] = Node(v, h[u], w); h[u] = stot; } double dis[200005]; int vis[200005], cnt[200005]; bool Spfa() { queue < int > q; for(int i = 1; i <= n + m; i ++) dis[i] = 0x3f3f3f3f; memset(vis, 0, sizeof(vis)); memset(cnt, 0, sizeof(cnt)); q.push(1); dis[1] = 0; while(!q.empty()) { int x = q.front(); vis[x] = 0; cnt[x] ++; q.pop(); if(cnt[x] > 15) return 0; for(int i = h[x]; i; i = Edge[i].nex) { int v = Edge[i].v; if(dis[v] > dis[x] + Edge[i].w) { dis[v] = dis[x] + Edge[i].w; if(!vis[v]) { vis[v] = 1; q.push(v); } } } } return 1; } double q[404][404]; int main() { while(scanf("%d%d%lf%lf", &n, &m, &L, &U) == 4) { memset(h, 0, sizeof(h)); stot = 0; L = log10(L); U = log10(U); for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) scanf("%lf", &q[i][j]), q[i][j] = log10(q[i][j]); for(int i = 1; i <= n; i ++) for(int j = 1; j <= m; j ++) { add(i, j + n, q[i][j] - L); add(j + n, i, U - q[i][j]); } if(Spfa()) printf("YES\n"); else printf("NO\n"); } return 0; }

