【最短路Dijistra】【一般堆优化】【配对堆优化】
突然觉得堆优化$O(log_n)$的复杂度很优啊,然而第n次忘记了$Dijistra$怎么写QAQ发现之前都是用的手写堆,这次用一下$stl$
#include<bits/stdc++.h> #define LL long long using namespace std; int n, m; struct Node { int v, nex, w; Node(int v = 0, int nex = 0, int w = 0) : v(v), nex(nex), w(w) { } } Edge[200001]; int h[100001], stot; void add(int u, int v, int w) { Edge[++stot] = Node(v, h[u], w); h[u] = stot; } struct QAQ { int u; LL dis; QAQ(int u = 0, LL dis = 0) : u(u), dis(dis) { } bool operator < (const QAQ a) const { return dis > a.dis; } }; LL dis[100001]; bool flag[100001]; void Diji(int s) { priority_queue < QAQ > q; for(int i = 1; i <= n; i ++) dis[i] = 0x3f3f3f3f; dis[s] = 0; q.push(QAQ(s, 0)); while(!q.empty()) { QAQ x = q.top(); q.pop(); int u = x.u; if(flag[u]) continue; flag[u] = 1; for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; if(!flag[v] && dis[v] > dis[u] + Edge[i].w) { dis[v] = dis[u] + Edge[i].w; q.push(QAQ(v, dis[v])); } } } } int main() { int s; scanf("%d%d%d", &n, &m, &s); for(int i = 1; i <= m; i ++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); add(a, b, c); } Diji(s); for(int i = 1; i <= n; i ++) printf("%lld ", dis[i]); return 0; }
然而遇到了这道题...
3040: 最短路(road)
Time Limit: 60 Sec Memory Limit: 200 MBSubmit: 4331 Solved: 1387
[Submit][Status][Discuss]
Description
N个点,M条边的有向图,求点1到点N的最短路(保证存在)。
1<=N<=1000000,1<=M<=10000000
Input
第一行两个整数N、M,表示点数和边数。
第二行六个整数T、rxa、rxc、rya、ryc、rp。
前T条边采用如下方式生成:
1.初始化x=y=z=0。
2.重复以下过程T次:
x=(x*rxa+rxc)%rp;
y=(y*rya+ryc)%rp;
a=min(x%n+1,y%n+1);
b=max(y%n+1,y%n+1);
则有一条从a到b的,长度为1e8-100*a的有向边。
后M-T条边采用读入方式:
接下来M-T行每行三个整数x,y,z,表示一条从x到y长度为z的有向边。
1<=x,y<=N,0<z,rxa,rxc,rya,ryc,rp<2^31
Output
一个整数,表示1~N的最短路。
Sample Input
0 1 2 3 5 7
1 2 1
1 3 3
2 3 1
Sample Output
HINT
【注释】
请采用高效的堆来优化Dijkstra算法。
Source
普通的堆优化会$MLE$,因为优先队列会把一个点弄进去很多次。
在网上发现了配对堆这个东西,可以包含优先队列的所有操作!!$tql$!!!
以下转载大米饼的博客:
[产品特色]
①沛堆堆(乱取的绰号)是一颗多叉树。
②包含Priority_Queue的所有功能,可用于优化最短路。
③属于可并堆,因此对于集合合并维护最值的问题很实用。
④速度快于一般的堆结构(左偏树,斜堆,随机堆……),具体快在这里:
这里就顺带引出它的基本操作啦:
·合并(Merge): O(1)
·插入(Insert/Push): O(1)
·修改值(Change): O(1)/O(logn)
·取出维护的最值(Top): O(1)
·弹出堆顶元素(Pop): O(logn)
[功能介绍]
①可并堆的灵魂——Merge操作
这里令人惊奇的是,配对堆只需要O(1)的时间完成这一步,具体做法为比较两个需要合并的堆的根的权值大小,然后就将那优先级较低(比如你要求大的在堆顶,那么权值越大,优先级越高)置为另一个点的儿子,即fa[v]=u,再将u向v建边即可。
②经典操作之一——插入(Push/Insert)操作
就很容易了,将插入元素新建为一个单独的节点作为一个堆,与当前的堆进行Merge操作就可以了。
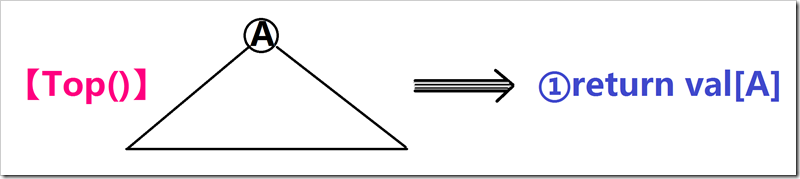
③经典操作之二——取最值(Top)操作
就直接用Root记录堆根,然后返回val[Root]就美妙完成任务。
④重要而具有特色的操作——修改操作(Change)
修改一个节点的的权值,那么怎么处理来继续保持配对堆的堆性质?首先将这个点和父节点的连边断掉,即fa[u]=0(由于父节点连边使用链式前向星,不方便删除,就不删除,但是这样并不会影响正确性,因为后文枚举一个点的儿子节点时,要确认某个点是它的儿子节点,不仅是要这个点能够有边指向这个儿子,同时需要这个儿子的fa[]中存储的就是这个节点)。
断掉与父亲的连边后,相当于形成两个堆,接下来进行一次Merge操作就好了。可以发现这个操作的时间复杂度是O(1),但有资料认为这个操作可能会破坏配对堆应有的结构(这"应有"的结构在下文会体现出来,它是Pop操作是O(logn)而不是O(n)的重要保证),结构改变后就会影响Pop的复杂度,使其向 O(n)退化,因此计算后认定其实修改操作从时间复杂度贡献分析来看,可能是O(logn)而不是O(1)。
⑤最缓慢但很重要的操作——弹出最值(Pop)操作
你会发现上文的操作都那么偷懒,几乎都是胡乱Merge一下,Merge函数又是随随便便连一条边就完事儿了……因此这个操作需要来收拾这个烂摊子。我们现在的任务是删除根节点,那么我们就要从它的儿子中选出合法继承人。如果直接将所有儿子挨个挨个Merge起来,那么这样很容易使得一个点有很多个儿子,从而影响后来的Pop操作时间,将O(logn)退化为O(n)。较快的做法是将子树两两合并,不断这样合并,最终形成一棵树,同理,这样之所以快是因为保证了后面pop操作时候点的儿子个数不会太多。
[要点尝鲜]
①链式前向星建边:
②Merge操作:
③Insert/Push操作:
④ChangeVal操作:
⑤Top操作:
⑥Pop操作:
[产品代码]
接下来一份简洁的代码,内容是将n个数排序。
其中的Stack是用来回收空间的。这里没有给出ChangVal函数,原因是这个函数适用于有特定位置的元素的修改,比如将数组插入堆,然后修改数组下表为i的元素权值。上文内容毫无保留地讲述了ChangVal的内容,直接打就是了。
同样的,如果要用来维护一些信息,比如Dijkstra的优化,那就在点的信息上添加记录最短路中点的编号之类的形成映射以达成快速取值的目的,其实呢和STL优先队列是一样的。
#include<stdio.h> #define go(i,a,b) for(int i=a;i<=b;i++) #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v) const int N=10000010; int n,a[N],b[N]; struct Stack { int S[N],s=0,k=0; int get(){return s?S[s--]:++k;} void Save(int index){S[++s]=index;} }Node,Edge; struct Pairing_Heap { int sz=0,fa[N],head[N],k,val[N],Root; int S[N],s;struct E{int v,next;}e[N]; void ADD(int u,int v){e[k=Edge.get()]=(E){v,head[u]};head[u]=k;} int Merge(int u,int v){val[u]>val[v]?u^=v^=u^=v:1;ADD(fa[v]=u,v);return u;} void Push(int Val){int u=Node.get();val[u]=Val;Root=Root?Merge(Root,u):u;} int Top(){return val[Root];} void Pop() { s=0;fo(i,head,Root)Edge.Save(i),fa[v]==Root?fa[S[++s]=v]=0:1; fa[Root]=head[Root]=0;Node.Save(Root);Root=0; int p=0;while(p<s){++p;if(p==s){Root=S[p];return;} int u=S[p],v=S[++p];S[++s]=Merge(u,v);} } }q; int main() { scanf("%d",&n); go(i,1,n)scanf("%d",a+i),q.Push(a[i]); go(i,1,n)printf("%d\n",q.Top()),q.Pop();return 0; }//Paul_Guderian
大米飘香的总结:
沛堆堆继承了斐波拉契堆的优秀操作复杂度,同时相比之下降低了空间复杂度和代码复杂度,这样优美高效的数据结构当然适合用在竞赛领域。如果谈到什么时候会用到沛堆堆,大米饼认为主要是两个方面——代替优先队列和代替常规的可并堆。常规可并堆如斜堆,随机堆和左偏树虽然代码更短,但是时间复杂度不够理想,再说了沛堆堆代码其实也很短的(这使得我们可以直接手写而不用冒风险去调用STL中的沛堆堆了)。最后这篇博文有一个小小的缺陷是,由于大米饼笨笨的,其实上文中ChangeVal是有局限的,其中修改值只能比原值小(如果越小优先级越高的话),因为如果修改为较大值,其操作就类似与Pop了,虽然个人认为时间复杂度由于都是O(logn)不会影响,但毕竟还没试验过,须谨慎使用。如果大米饼出错了或者出现冗余,希望来浏览的人加以指出批评。
然而本人并不打算学透,而且有stl的配对堆,所以背背代码吧~~
#include<bits/stdc++.h> #include<ext/pb_ds/priority_queue.hpp> #define LL long long using namespace std; using namespace __gnu_pbds; typedef __gnu_pbds::priority_queue < pair < LL, int > > heap; heap::point_iterator id[1000005]; int n, m; struct Node { int v, nex, w; Node(int v = 0, int nex = 0, int w = 0) : v(v), nex(nex), w(w) { } } Edge[10000001]; int h[1000001], stot; void add(int u, int v, int w) { Edge[++stot] = Node(v, h[u], w); h[u] = stot; } LL dis[1000001]; bool flag[1000001]; void Diji() { heap q; for(int i = 2; i <= n; i ++) dis[i] = 0x3f3f3f3f; id[1] = q.push(make_pair(0, 1)); while(!q.empty()) { int x = q.top().second; q.pop(); if(x == n) break; for(int i = h[x]; i; i = Edge[i].nex) { int v = Edge[i].v; if(dis[v] > dis[x] + Edge[i].w) { dis[v] = dis[x] + Edge[i].w; if(id[v] != 0) q.modify(id[v], make_pair(-dis[v], v)); else id[v] = q.push(make_pair(-dis[v], v)); } } } } int main() { scanf("%d%d", &n, &m); int T, rxa, rxc, rya, ryc, rp; scanf("%d%d%d%d%d%d", &T, &rxa, &rxc, &rya, &ryc, &rp); int x = 0, y = 0, z = 0; for(int i = 1; i <= T; i ++) { int a, b; x = ((long long)x * rxa + rxc) % rp; y = ((long long)y * rya + ryc) % rp; a = min(x % n + 1, y % n + 1); b = max(y % n + 1, y % n + 1); add(a, b, 1e8 - 100 * a); } for(int i = 1; i <= m - T; i ++) { int a, b, c; scanf("%d%d%d", &a, &b, &c); add(a, b, c); } Diji(); printf("%lld", dis[n]); return 0; }