【洛谷】3953:逛公园【反向最短路】【记忆化搜索(DP)统计方案】
题目描述
策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图,且没有 自环和重边。其中1号点是公园的入口,N号点是公园的出口,每条边有一个非负权值, 代表策策经过这条边所要花的时间。
策策每天都会去逛公园,他总是从1号点进去,从N号点出来。
策策喜欢新鲜的事物,它不希望有两天逛公园的路线完全一样,同时策策还是一个 特别热爱学习的好孩子,它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到N号点的最短路长为d,那么策策只会喜欢长度不超过d+K的路线。
策策同学想知道总共有多少条满足条件的路线,你能帮帮它吗?
为避免输出过大,答案对P取模。
如果有无穷多条合法的路线,请输出−1。
输入输出格式
输入格式:
第一行包含一个整数 T, 代表数据组数。
接下来T组数据,对于每组数据: 第一行包含四个整数 N,M,K,P,每两个整数之间用一个空格隔开。
接下来M行,每行三个整数ai,bi,ci,代表编号为ai,bi的点之间有一条权值为 ci的有向边,每两个整数之间用一个空格隔开。
输出格式:
输出文件包含 T 行,每行一个整数代表答案。
输入输出样例
2 5 7 2 10 1 2 1 2 4 0 4 5 2 2 3 2 3 4 1 3 5 2 1 5 3 2 2 0 10 1 2 0 2 1 0
3 -1
说明
【样例解释1】
对于第一组数据,最短路为 3。 1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5为 33 条合法路径。
【测试数据与约定】
对于不同的测试点,我们约定各种参数的规模不会超过如下
| 测试点编号 | T | N | M | K | 是否有0边 |
|---|---|---|---|---|---|
| 1 | 5 | 5 | 10 | 0 | 否 |
| 2 | 5 | 1000 | 2000 | 0 | 否 |
| 3 | 5 | 1000 | 2000 | 50 | 否 |
| 4 | 5 | 1000 | 2000 | 50 | 否 |
| 5 | 5 | 1000 | 2000 | 50 | 否 |
| 6 | 5 | 1000 | 2000 | 50 | 是 |
| 7 | 5 | 100000 | 200000 | 0 | 否 |
| 8 | 3 | 100000 | 200000 | 50 | 否 |
| 9 | 3 | 100000 | 200000 | 50 | 是 |
| 10 | 3 | 100000 | 200000 | 50 | 是 |
对于 100%的数据, 1≤P≤109,1≤ai,bi≤N,0≤ci≤1000。
数据保证:至少存在一条合法的路线。
被誉为是noip2017最难的一道题了...以前写过,但那时基本就是对着标程抄,还没有理解。
对记忆化搜索本来做得不好,希望能有一些更深入的理解了吧....
首先观察数据范围,明显是一道与$K$有关的DP。可以想到定义$dp[u][k]$表示$u$到$n$的距离是$dis[u]+k$的方案数。所以答案就是$\sum_{i=0}^{k}{dp[1][i]}$所以还要建反向边预处理出每个点到$n$的最短路$dis$。
然后发现,正向跑时,$dp[u][k]$可以从所有它可以到达的$v$更新过来。
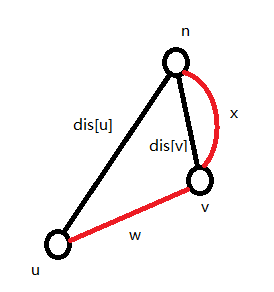
如图,已经确定了在$u$点时多出的$k$,那么如果要走到$v$点,可以确定$v$点多出的$k'$,通过$x+w-dis[u]=k$和$x-dis[v]=k'$可得出$k'=dis[u]+k-w-dis[v]$,然后就可以往下记忆化搜索来更新$dis[u][k]$了。初值$dp[u][0]=1$。
如何判0环?我们在搜索的时候定一个$fl[u][k]$标记,如果正在搜索中$fl=1$,如果搜索完了$fl=2$,如果同一个状态$[u][k]$第二次搜到的时候还在搜索中,即$fl[u][k]=1$,那么搜索过程中出现了0环,直接打标记退出即可。
#include<bits/stdc++.h> using namespace std; int n, p, m, k; struct Node { int v, nex, w; Node(int v = 0, int nex = 0, int w = 0) : v(v), nex(nex), w(w) { } } Edge[400004]; int h[100005], stot; void add(int u, int v, int w) { Edge[++stot] = Node(v, h[u], w); h[u] = stot; } int dis[100005], vis[100005]; void Spfa() { queue < int > q; memset(vis, 0, sizeof(vis)); memset(dis, 0x3f3f3f3f, sizeof(dis)); q.push(n); vis[n] = 1; dis[n] = 0; while(!q.empty()) { int u = q.front(); q.pop(); vis[u] = 0; for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; if(dis[v] > dis[u] + Edge[i].w) { dis[v] = dis[u] + Edge[i].w; if(!vis[v]) vis[v] = 1, q.push(v); } } } } int dp[100005][55]; int fl[100005][55], flag; int dfs(int u, int k) { if(fl[u][k] == 1 || flag == -1) return flag = -1; if(fl[u][k] == 2) return dp[u][k]; fl[u][k] = 1; for(int i = h[u]; i; i = Edge[i].nex) { int v = Edge[i].v; int to = dis[u] + k - Edge[i].w - dis[v]; if(to > k || to < 0) continue; dp[u][k] = (dp[u][k] + dfs(v, to)) % p; if(flag == -1) return -1; } fl[u][k] = 2; return dp[u][k]; } int a[200005], b[200005], c[200005]; int main() { int T; scanf("%d", &T); while(T --) { memset(h, 0, sizeof(h)); stot = 0; flag = 1; scanf("%d%d%d%d", &n, &m, &k, &p); for(int i = 1; i <= m; i ++) { scanf("%d%d%d", &a[i], &b[i], &c[i]); add(b[i], a[i], c[i]); } Spfa(); memset(h, 0, sizeof(h)); stot = 0; for(int i = 1; i <= m; i ++) add(a[i], b[i], c[i]); int ans = 0; memset(fl, 0, sizeof(fl)); memset(dp, 0, sizeof(dp)); dp[n][0] = 1; for(int i = 0; i <= k; i ++) ans = (long long)(ans + dfs(1, i)) % p; if(~flag) printf("%d\n", ans); else printf("-1\n"); } return 0; }


