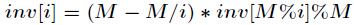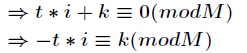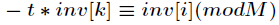【线性求逆元】
转自https://blog.csdn.net/qq_34564984/article/details/52292502
其实有些题需要用到


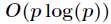
如果对于一个1000000级别的素数
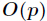
它的推导过程如下,设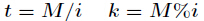
对上式两边同时除
再把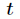
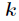
初始化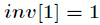


另外


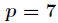
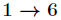
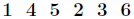
然后附上我自己的代码:(把$M-$省略了所以要%+%)
inv[0] = inv[1] = 1; for(int i = 2; i < mod; i ++) inv[i] = ((-(mod / i) * inv[mod % i]) % mod + mod) % mod;