【洛谷】NOIP提高组模拟赛Day2【动态开节点/树状数组】【双头链表模拟】
题目背景
炎炎夏日还没有过去,Agent们没有一个想出去外面搞事情的。每当ENLIGHTENED总部组织活动时,人人都说有空,结果到了活动日,却一个接着一个咕咕咕了。只有不咕鸟Lyn_king一个人冒着太阳等了半个多小时,然后居然看到连ENLIGHTENED行动参谋都咕咕咕了,果然咕咕咕是人类的本性啊。
题目描述
作为一个ENLIGHTENED行动指挥,自然不想看到这一点,于是他偷取到了那些经常咕咕咕的Agent的在下来N天的活动安排表,并且叫上了你来整理。在整理过程中,ENLIGHTENED行动指挥对你说了M条命令,命令操作如下。
- 输入0 a b,这代表在第a天到第b天,有一名
Agent要咕咕咕。 - 输入1 a,这代表
ENLIGHTENED行动指挥询问你根据目前的信息,在第a天有多少名Agent会咕咕咕。
作为同是不咕鸟的你,也想要惩戒那些经常咕咕咕的人,所以,请协助完成ENLIGHTENED行动指挥完成整理,并且在他每次询问时,输出正确的答案。
输入输出格式
输入格式:
第一行输入两个整数输N,M, 下来M行,每行输入一个命令,命令格式见题目描述。
输出格式:
对于每一次询问的操作,都要输出询问的答案。答案之间用换行隔开。
输入输出样例
说明
对于20%的数据N,M≤10
对于40%的数据N,M≤103
对于60%的数据N,M≤105
对于100%的数据1≤a,b≤N≤107,M≤4∗105
这道题签到题,难点在数据范围,普通线段树肯定做不了,所以采用动态开节点,要查询的才建立节点即可。
然而一开始疯狂乱错,原因是中间某个地方写了+=后面又加了一遍...
也可以用树状数组做,代码非常简洁。
#include<bits/stdc++.h> using namespace std; int n, m; struct Node { Node *ls, *rs; int sum, tag; } pool[32*400005], *tail = pool, *zero, *root; Node *newnode() { Node *nd = ++ tail; nd -> ls = zero; nd -> rs = zero; nd -> sum = 0; nd -> tag = 0; return nd; } void push_down(Node *nd, int l, int r) { if(nd -> tag) { int mid = (l + r) >> 1; if(nd -> ls == zero) nd -> ls = newnode(); nd -> ls -> sum = nd -> ls -> sum + nd -> tag * (mid - l + 1); if(nd -> rs == zero) nd -> rs = newnode(); nd -> rs -> sum = nd -> rs -> sum + nd -> tag * (r - mid); nd -> ls -> tag += nd -> tag; nd -> rs -> tag += nd -> tag; nd -> tag = 0; } } void add(Node *nd, int l, int r, int L, int R, int d) { if(l >= L && r <= R) { nd -> sum = nd -> sum + (r - l + 1) * d; nd -> tag += d; return ; } push_down(nd, l, r); int mid = (l + r) >> 1; if(L <= mid) { if(nd -> ls == zero) nd -> ls = newnode(); add(nd -> ls, l, mid, L, R, d); } if(R > mid) { if(nd -> rs == zero) nd -> rs = newnode(); add(nd -> rs, mid + 1, r, L, R, d); } } int query(Node *nd, int l, int r, int pos) { if(l == r) return nd -> sum; push_down(nd, l, r); int mid = (l + r) >> 1; if(pos <= mid) return query(nd -> ls, l, mid, pos); else return query(nd -> rs, mid + 1, r, pos); } int main() { zero = ++ tail; zero -> ls = zero; zero -> rs = zero; zero -> sum = 0; zero -> tag = 0; scanf("%d%d", &n, &m); root = newnode(); for(int i = 1; i <= m; i ++) { int opt, l, r; scanf("%d", &opt); if(opt == 0) { scanf("%d%d", &l, &r); add(root, 1, n, l, r, 1); } else { scanf("%d", &l); printf("%d\n", query(root, 1, n, l)); } } return 0; }
树状数组:
#include<bits/stdc++.h> using namespace std; int n, m; int lowbit(int x) { return x & -x; } int pre[10000005]; void add(int pos, int d) { for(int i = pos; i <= n; i += lowbit(i)) pre[i] += d; } int query(int pos) { int ans = 0; for(int i = pos; i; i -= lowbit(i)) ans += pre[i]; return ans; } int main() { scanf("%d%d", &n, &m); for(int i = 1; i <= m; i ++) { int opt, l, r; scanf("%d", &opt); if(opt == 0) { scanf("%d%d", &l, &r); add(l, 1); add(r+1, -1); } else { scanf("%d", &l); printf("%d\n", query(l)); } } return 0; }
题目背景
某地ENLIGHTENED的XM研究所正在研究Portal的处理法则,想要揭示XM能量的来源以及应用XM能量。ENLIGHTENED的首席科学家Jacks发现其能量的运算法则以及运算方法,但是方法十分复杂,仅靠人手工计算是很难算出答案的,所以它需要你协助他完成计算。
题目描述
Portal计算XM能量是通过个2个栈(0号栈,1号栈)实现的,它把对XM能量的操作如下
PUSH X NUM
把NUMNUM加入到X号栈的栈顶。
POP X
把XX号栈的栈顶元素删除。
ADD X
取出0号栈和1号栈的元素各一个,并且把它的和放入X号栈。
SUB X
取出0号栈和1号栈的元素各一个,并且把它的差的绝对值放入X号栈。
DEL X
清空X号栈中所有元素不管栈是否为空。
MOVE X Y
循环操直到Y号栈为空,把Y号栈的栈顶元素加入到X号栈,删除Y号栈的栈顶元素。
数据保证X和Y不相同
SWAP
将两个栈的所有元素调换。
END
代表命令结束,并且分两行分别输出0号栈和1号栈由栈顶到栈底的元素的值,若栈内无元素,输出NONE。数据保证指令以END结束且仅有一个END,并且也需要输出SUCCESS。
AKNOI
等为无效操作,无效操作后不接数字。
更正不会有类似无效操作
对于每一行指令,若当前指令成功执行输出SUCCESS,若取出或删除元素时栈内为空或者没有对应指令输出UNSUCCESS并且不执行该行指令。
输入输出格式
输入格式:
输入若干行指令,以END指令结束
输出格式:
对于每一次操作,都要对应输出SUCCESS或者UNSUCCESS,对于END根据指令描述输出栈内元素。
输入输出样例
PUSH 0 10 PUSH 0 20 PUSH 0 30 PUSH 0 40 PUSH 1 50 PUSH 1 60 ADD 0 ADD 0 ADD 0 END
SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS UNSUCCESS SUCCESS 150 30 20 10 NONE
PUSH 0 10 PUSH 0 20 PUSH 0 30 PUSH 0 40 PUSH 1 50 PUSH 1 60 MOVE 0 1 END
SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS SUCCESS 50 60 40 30 20 10 NONE
说明
对于20%的数据 数据保证不会出现MOVE/SWAP操作,命令总数 ≤ 100
对于40%的数据 命令总数 ≤ 1000
对于60%的数据 数据保证MOVE/SWAP的操作次数不会超过10000次,命令总数 ≤ 10^5
对于100%的数据 0 ≤ X,Y ≤ 1,命令总数≤10^6
数据保证无论任何情况,栈中元素的值X满足0≤ x ≤2^63-1
学到了新东西!!链表模拟。
一开始总觉得链表全都是像建边的邻接链表那样,做了这道题有所感悟!
这道题要求满足两个栈的同时维护,比较困难的操作有$swap$和$move$以及$del$,暴力模拟都需要$O(n)$。所以这里就是链表模拟的套路了?
两个栈之间建立新节点2作为过渡,所有操作都用双头链表,新节点的$pre$连第一个栈,$nex$连第二个栈。

上面是链接链表的主要操作。$push$就是把要插入的值插入到哪两个点之间。
$swap$:感谢$Abyssful$的教导!如何快速交换两个数组内所有的值?记录$stk[0/1]$表示0数组和1数组当前存的是哪个数组内的东西。初始化是$stk[0]=0,stk[1]=1$,访问时$a[stk[0]][...],a[stk[1]][...]$来分别访问两个数组。这道题同理,只是因为用链表储存了两个栈,所以通过$stk[0/1]$来确定访问$pre[2]$还是$nex[2]$。
$move$:将一个栈所有元素移到另一个栈中,并且是边从栈顶取边移过去。所以首先要把两个栈顶连起来,再看是哪边移到哪边,$y->x$,就把$y$的尾和新节点相连,再把$y$那边清空即可,$x$同理。判断一下是0还是1就可以判断是移到哪里了。
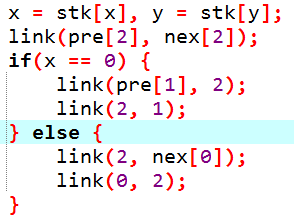
$del$:直接把要清空的那边直接连到新节点就行了。
输出就沿着双头链表走到头就行了。
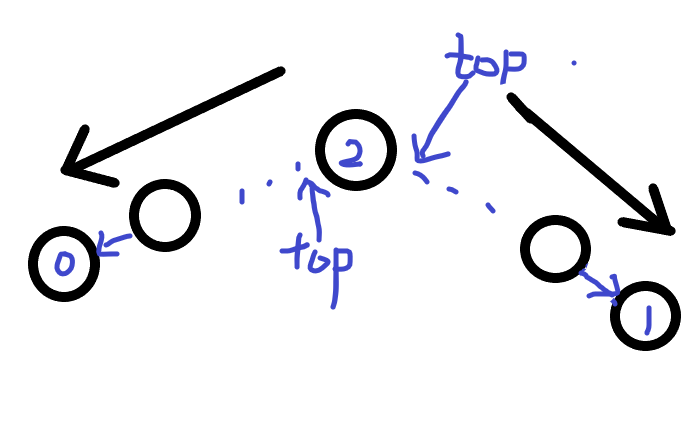
2020.11.3更新
重新看一遍果然好难想,画了个图更好理解,$pre[2]$之前到$0$节点的是$0$栈,$nex[2]$之后到$1$节点是$1$栈。栈顶都是在靠近$2$节点的位置,也就是$pre[2]$和$nex[2]$,所以最后输出是从$2$节点分别向两个方向走到对应的头节点。
但是$move$操作会将其中一个栈翻转,也就是栈底变为栈顶。那么此时只需要把$pre[2]$和$nex[2]$连接起来(两种类型都必须合并),再将对应栈底插入$2$节点前或后就行了,栈底分别是$nex[0]$和$pre[1]$,改变了栈底的位置后,输出按照改变后的栈的规则输出就能把之前的数据一起带出来(比如输出$1$栈最开始用$nex$输出,改变后用$pre$输出即可),这就是双头链表在这道题中最大的作用。
复健愉快!
#include<bits/stdc++.h> #define LL long long using namespace std; char s[105]; int nex[1000005], pre[1000005]; LL val[1000005]; int cnt = 2; void link(int u, int v) { nex[u] = v; pre[v] = u; } void lpush(int u, int v, LL w) { val[++cnt] = w; link(u, cnt); link(cnt, v); } void push(int x, LL w) { if(x == 0) lpush(pre[2], 2, w); else lpush(2, nex[2], w); } LL pop(int u) { link(pre[u], nex[u]); return val[u]; } void print(int u) { if(u) { if(nex[2] == 1) { printf("NONE\n"); return ; } for(int i = nex[2]; i != 1; i = nex[i]) printf("%lld ", val[i]); printf("\n"); } else { if(!pre[2]) { printf("NONE\n"); return ; } for(int i = pre[2]; i != 0; i = pre[i]) printf("%lld ", val[i]); printf("\n"); } } int stk[2]; void print() { if(stk[0]) { print(1); print(0); } else { print(0); print(1); } } bool sov(char *s) { int x, y; LL num; if(s[0] == 'P') { if(s[1] == 'U') { scanf("%d%lld", &x, &num); x = stk[x]; push(x, num); } else { scanf("%d", &x); x = stk[x]; if(x == 0) { if(pre[2] == 0) return 0; pop(pre[2]); } else { if(nex[2] == 1) return 0; pop(nex[2]); } } } else if(s[0] == 'A') { scanf("%d", &x); x = stk[x]; if(pre[2] == 0 || nex[2] == 1) return 0; push(x, pop(pre[2]) + pop(nex[2])); } else if(s[0] == 'S') { if(s[1] == 'U') { scanf("%d", &x); x = stk[x]; if(pre[2] == 0 || nex[2] == 1) return 0; push(x, abs(pop(pre[2]) - pop(nex[2]))); } else { swap(stk[0], stk[1]); } } else if(s[0] == 'D') { scanf("%d", &x); x = stk[x]; if(x == 0) link(0, 2); else link(2, 1); } else if(s[0] == 'M') { scanf("%d%d", &x, &y); x = stk[x], y = stk[y]; link(pre[2], nex[2]); if(x == 0) { link(pre[1], 2); link(2, 1); } else { link(2, nex[0]); link(0, 2); } } return 1; } int main() { stk[0] = 0, stk[1] = 1; link(0, 2); link(2, 1); while(~scanf("%s", s)) { if(s[0] == 'E') { puts("SUCCESS"); print(); break; } if(sov(s)) puts("SUCCESS"); else puts("UNSUCCESS"); } return 0; }
题目背景
XM大战如期而至,Agent们齐聚一地,展开最后的对决。对战有很多种方式,有些复杂的方式可以获得更高的分数。可惜ENLIGHTENED的人并不怎么聪明,只会简单的hack,所以ENLIGHTENED行动指挥找到了你来做他们的总参谋。
题目描述
地图上有N个Portal,现在某一名Agent的任务是占领该地图上的M个Portal,这名Agent占领第i个Portal可以得到的分数为A[i],除了直接占领,还有其他的K种加分方式,对于着N个Portal,在占领完第X[i]个Portal后占领第Y[i]个Portal可以获得B[i]的加分,加分可能会有重复。Agent希望他可以为团队争取更多的分数,所以请求作为大战参谋的你来帮助他。
输入输出格式
输入格式:
第一行是输入三个整数N,M,K 第二行输入是N个数,第i个数代表A[i]的值。 下面K行每行有3个整数X[i],Y[i],C[i],表示在占领完第X[i]个Portal后占领第Y[i]个Portal可以获得B[i]的加分
输出格式:
输出仅一行一个整数,为该名Agent可以获得的最大分数值。
输入输出样例
说明
对于20%的数据 1≤M≤N≤4,0≤A[i],B[i]≤103
对于40%的数据 1≤M≤N≤8,0≤A[i],B[i]≤105
对于60%的数据 1≤M≤N≤12,0≤A[i],B[i]≤107
对于100%的数据 1≤M,X[i],Y[i]≤N≤18,0≤K≤N^2−N,0≤A[i],B[i]≤10^9
一道比较好想+写的状压DP,然而一开始很慌,题两次没看清楚。
分数累加的意思是如果有重复的$a$和$b$,他们的分数是可以累加起来的。
而$a$到$b$是严格要求$b$在$a$后面第一个,所以状态还要定义一个最后占领的。然后转移就行了。
#include<bits/stdc++.h> #define LL long long #define RG register using namespace std; int n, m, k; LL dp[(1<<18) + 1][20], qwq[20], zty[20][20]; int cnt[(1<<18) + 1]; int countt(int s) { int num = 0; while(s) { num += s & 1; s >>= 1; } return num; } LL cot(int s) { LL ans = 0; for(int i = 1; i <= n; i ++) if((s >> (i-1)) & 1) ans += qwq[i]; return ans; } void init() { for(int i = 0; i < (1 << n); i ++) cnt[i] = countt(i); } int main() { scanf("%d%d%d", &n, &m, &k); init(); for(int i = 1; i <= n; i ++) scanf("%lld", &qwq[i]); for(int i = 1; i <= k; i ++) { int a, b; LL c; scanf("%d%d%lld", &a, &b, &c); zty[a][b] += c; } for(RG int s = 0; s < (1 << n); s ++) { if(cnt[s] >= m) continue; for(RG int i = 1; i <= n; i ++) if(!((s >> (i-1)) & 1)) for(RG int j = 1; j <= n; j ++) if((s >> (j-1)) & 1) if(zty[j][i]) dp[s|(1 << (i-1))][i] = max(dp[s|(1 << (i-1))][i], dp[s][j] + zty[j][i]); } LL ans = 0; for(int s = 0; s < (1 << n); s ++) for(int i = 1; i <= n; i ++) if(cnt[s] == m) ans = max(ans, dp[s][i] + cot(s)); printf("%lld", ans); return 0; }


