【8.27校内测试】【树状数组+按余数分类】【最小生成树+树链剖分+线段树】

我们发现，$e$非常小，而对于不同的$e$，因为在原串中都会被复制很多次，$e$中的每一个位置可以对应原串中多个位置，而这些位置%$|e|$的值都是一样的。而我们把问题转换，就变成了在原串中求区间中每个对应位置中出现了多少个$e$中对应位置的值。可以用树状数组维护，不过为了具体表示每一种位置的不同，需要用$pre[pos][x][yu][mod]$分别表示原序列中的位置，要查询的值，当前对应的余数和模数。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

char s[100005];
int a[100005], pre[100005][4][11][11], n;

int lowbit ( int x ) {
    return x & -x;
}

void modify ( int pos, int x, int yu, int mod, int d ) {
    for ( int i = pos; i <= n; i += lowbit ( i ) )
        pre[i][x][yu][mod] += d;
}

void modify ( int x, int y ) {
    for ( int mod = 1; mod <= 10; mod ++ ) {
        int yu = x % mod;
        modify ( x, a[x], yu, mod, -1 );
        modify ( x, y, yu, mod, 1 );
    }
    a[x] = y;
}

int query ( int pos, int x, int t, int mod ) {
    int ans = 0;
    for ( int i = pos; i; i -= lowbit ( i ) )
        ans += pre[i][x][t][mod];
    return ans;
}

int query ( int l, int r, int qaq[], int len ) {
    int ans = 0;
    for ( int i = 1; i <= len; i ++ ) {
        int yu = ( l + i - 1 ) % len;
        ans += query ( r, qaq[i], yu, len ) - query ( l - 1, qaq[i], yu, len );
    }
    return ans;
}

int count ( char x ) {
    if ( x == 'A' ) return 1;
    else if ( x == 'G' ) return 2;
    else if ( x == 'T' ) return 3;
    else if ( x == 'C' ) return 4;
}

int main ( ) {
    freopen ( "evolution.in", "r", stdin );
    freopen ( "evolution.out", "w", stdout );
    scanf ( "%s", s + 1 );
    n = strlen ( s + 1 );
    for ( int i = 1; i <= n; i ++ ) {
        a[i] = count ( s[i] );
    }
    for ( int mod = 1; mod <= 10; mod ++ )
        for ( int i = 1; i <= n; i ++ ) {
            int yu = i % mod;
            modify ( i, a[i], yu, mod, 1 );
        }
    int q;
    scanf ( "%d", &q );
    while ( q -- ) {
        int opt;
        scanf ( "%d", &opt );
        if ( opt == 1 ) {
            int x; char ch;
            scanf ( "%d %c", &x, &ch );
            int t = count ( ch );
            modify ( x, t );
        } else {
            int l, r; char qwq[15]; int qaq[15] = {0};
            scanf ( "%d%d ", &l, &r );
            scanf ( "%s", qwq + 1 );
            for ( int i = 1; i <= strlen ( qwq + 1 ); i ++ )
                qaq[i] = count ( qwq[i] );
            int ans = query ( l, r, qaq, strlen ( qwq + 1 ) );
            printf ( "%d\n", ans );
        }
    }
    return 0;
}

我们将问题转换，发现生成最小生成树中有如下性质：

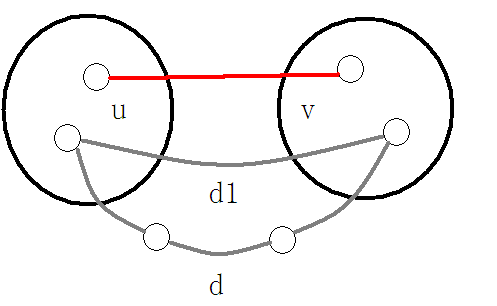
如图两个黑色的圈是我们当前两个处理出来的并查集。如果我们要使$u$到$v$这条红色的边在最小生成树中永远出现，那么它就一定要比这两个并查集中其他任意点之间路径中边权最大的那条小，不然就可以用其它的边代替它连接这两个并查集。

而建成最小生成树后，我们发现$u$到$v$间的简单路径中边权最大的那条边就是我们要求的边。

所以对于一条非最小生成树上的边来说，我们找到它两个端点在最小生成树上路径间的最大边，-1就是它的最大可行改变值。

而对于最小生成树中已经建成的边，我们可以发现如下性质：

 

如图，如果画了×的那条边要永远在最小生成树中，说明连接两个红框并查集的其他边都不能被他替代，意味着，所有像灰边这样当前不在最小生成树中但是可以连接两个并查集的所有边的最小边权，都要大于画了×的这条边的边权，不然这条边就可以被其他灰边替代。

而我们又发现，所有像这种不在最小生成树中的灰边会影响的树边就是灰边两端点间简单路径中的所有边。所以我们在处理每一条灰边时，去更新两端点简单路径中的所有边的最小值，最后减一即可。

而以上提到的操作都可以用树链剖分和线段树维护...

两棵线段树分别维护树边和非树边需要的值...

调成粑粑叻...

 

#include<iostream>
#include<cstdio>
#include<algorithm>
#define oo 1000000001
using namespace std;

int n, m;

struct Edge {
    int u, v, w, nex, tag = 0, id;
    Edge ( int u = 0, int v = 0, int w = 0, int nex = 0, int id = 0 ) :
        u ( u ), v ( v ), w ( w ), nex ( nex ), id ( id ) { }
} Init[200005], edge[200005];
bool cmp1 ( Edge a, Edge b ) { return a.w < b.w; }
bool cmp2 ( Edge a, Edge b ) { return a.id < b.id; }

int init, h_init[100005];
void add_init ( int u, int v, int w, int id ) {
    Init[++init] = Edge ( u, v, w, h_init[u], id );
    h_init[u] = init;
}

int stot, h[100005];
void add_edge ( int u, int v, int w ) {
    edge[++stot] = Edge ( u, v, w, h[u] );
    h[u] = stot;
}

int fa[100005];
int find ( int x ) { if ( x != fa[x] ) return fa[x] = find ( fa[x] ); return fa[x]; }
void unionn ( int x, int y ) { fa[x] = y; }

void Kruskal ( ) {
    for ( int i = 1; i <= n; i ++ ) fa[i] = i;
    sort ( Init + 1, Init + 1 + init, cmp1 );
    for ( int i = 1; i <= init; i ++ ) {
        int u = Init[i].u, v = Init[i].v, w = Init[i].w;
        int uu = find ( u ), vv = find ( v );
        if ( uu != vv ) { unionn ( uu, vv ); add_edge ( u, v, w ); add_edge ( v, u, w ); Init[i].tag = 1; } 
    }
}

int siz[100005], f[100005], dep[100005], son[100005], s[100005];
void dfs1 ( int u, int ff ) {
    siz[u] = 1; f[u] = ff; dep[u] = dep[ff] + 1;
    for ( int i = h[u]; i; i = edge[i].nex ) {
        int v = edge[i].v; if ( v == ff ) continue;
        dfs1 ( v, u );
        siz[u] += siz[v];
        if ( siz[v] > siz[son[u]] ) son[u] = v, s[u] = edge[i].w;
    }
}

int top[100005], in[100005], seq[100005], dis[100005], ti;
void dfs2 ( int u, int t ) {
    top[u] = t; in[u] = ++ ti; seq[ti] = dis[u];
    if ( son[u] ) { dis[son[u]] = s[u]; dfs2 ( son[u], t ); }
    for ( int i = h[u]; i; i = edge[i].nex ) {
        int v = edge[i].v; if ( v == f[u] || v == son[u] ) continue;
        dis[v] = edge[i].w; dfs2 ( v, v );
    }
}

int TR[400005], ZTY[400005], tag[400005];
void update ( int nd ) { TR[nd] = max ( TR[nd << 1], TR[nd << 1 | 1] ); }
void push_down ( int nd ) {
    if ( tag[nd] != oo ) {
        ZTY[nd << 1] = min ( ZTY[nd << 1], tag[nd] ); ZTY[nd << 1 | 1] = min ( ZTY[nd << 1 | 1], tag[nd] );
        tag[nd << 1] = min ( tag[nd << 1], tag[nd] ); tag[nd << 1 | 1] = min ( tag[nd << 1 | 1], tag[nd] );
        tag[nd] = oo;
    }
}

void build ( int nd, int l, int r ) {
    tag[nd] = oo;
    if ( l == r ) {
        TR[nd] = seq[l];
        ZTY[nd] = oo;
        return ;
    }
    int mid = ( l + r ) >> 1;
    build ( nd << 1, l, mid );
    build ( nd << 1 | 1, mid + 1, r );
    update ( nd );
}

int query_MA ( int nd, int l, int r, int L, int R ) {
    if ( l >= L && r <= R ) return TR[nd];
    int ans = 0; int mid = ( l + r ) >> 1;
    if ( L <= mid ) ans = max ( ans, query_MA ( nd << 1, l, mid, L, R ) );
    if ( R > mid ) ans = max ( ans, query_MA ( nd << 1 | 1, mid + 1, r, L, R ) );
    return ans;
}

void modify ( int nd, int l, int r, int L, int R, int d ) {
    if ( l >= L && r <= R ) { ZTY[nd] = min ( d, ZTY[nd] ); tag[nd] = min ( tag[nd], d ); return ; }
    push_down ( nd ); int mid = ( l + r ) >> 1;
    if ( L <= mid ) modify ( nd << 1, l, mid, L, R, d );
    if ( R > mid ) modify ( nd << 1 | 1, mid + 1, r, L, R, d );
}

int query_MI ( int nd, int l, int r, int pos ) {
    if ( l == r ) return ZTY[nd];
    push_down ( nd );
    int mid = ( l + r ) >> 1;
    if ( pos <= mid ) return query_MI ( nd << 1, l, mid, pos );
    else return query_MI ( nd << 1 | 1, mid + 1, r, pos ) ;
}

int query_MA ( int u, int v ) {
    int ans = 0;
    if ( dep[top[u]] < dep[top[v]] ) swap ( u, v );
    while ( top[u] != top[v] ) {
        ans = max ( ans, query_MA ( 1, 1, n, in[top[u]], in[u] ) );
        u = f[top[u]];
        if ( dep[top[u]] < dep[top[v]] ) swap ( u, v );
    }
    if( dep[v] > dep[u] ) swap ( u, v );
    ans = max ( ans, query_MA ( 1, 1, n, in[v]+1, in[u] ) );
    return ans;
}

int modify_MI ( int u, int v, int w ) {
    int ans = 0;    
    while ( top[u] != top[v] ) {
         if ( dep[top[u]] < dep[top[v]] ) swap ( u, v );
        modify ( 1, 1, n, in[top[u]], in[u], w );
        u = f[top[u]];
    }
    if ( dep[v] > dep[u] ) swap ( u, v );
    modify ( 1, 1, n, in[v]+1, in[u], w );
    return ans;
}

int las[100005];
int main ( ) {
    freopen ( "mst.in", "r", stdin );
    freopen ( "mst.out", "w", stdout );
    scanf ( "%d%d", &n, &m );
    for ( int i = 1; i <= m; i ++ ) {
        int u, v, w;
        scanf ( "%d%d%d", &u, &v, &w );
        add_init ( u, v, w, i );
    }
    Kruskal ( );
    sort ( Init + 1, Init + 1 + init, cmp2 );
    dfs1 ( 1, 0 );
    dfs2 ( 1, 1 );
    build ( 1, 1, n );
    for ( int i = 1; i <= m; i ++ )
        if ( !Init[i].tag ) {
            int u = Init[i].u, v = Init[i].v, w = Init[i].w;
            las[i] = query_MA ( u, v ) - 1;
            modify_MI ( u, v, w - 1 );
        }
    for ( int i = 1; i <= m; i ++ )
        if ( Init[i].tag ) {
            int u = Init[i].u, v = Init[i].v;
            if ( dep[u] < dep[v] ) swap ( u, v );
            las[i] = query_MI ( 1, 1, n, in[u] );
            if ( las[i] == oo ) las[i] = -1;
        }
    for ( int i = 1; i <= m; i ++ ) printf ( "%d ", las[i] );
    return 0;
}