【8.23校内测试】【贪心】【线段树优化DP】

$m$的数据范围看起来非常有问题？？仔细多列几个例子可以发现，在$m<=5$的时候，只要找到有两行状态按位$&$起来等于$0$，就是可行方案，如果没有就不行。

 

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int cnt[1<<4+1], n, m;

int main ( ) {
    freopen ( "prob.in", "r", stdin );
    freopen ( "prob.out", "w", stdout );
    int T;
    scanf ( "%d", &T );
    while ( T -- ) {
        memset ( cnt, 0, sizeof ( cnt ) );
        scanf ( "%d%d", &n, &m );
        for ( int i = 1; i <= n; i ++ ) {
            int t = 0;
            for ( int j = 0; j < m; j ++ ) {
                int a;
                scanf ( "%d", &a );
                t |= a << j;
            }
            cnt[t] ++;
        }
        int flag = 0;
        int tot = ( 1 << m ) - 1;
        for ( int i = 0; i <= tot; i ++ )
            for ( int j = i + 1; j <= tot; j ++ ) {
                if ( !cnt[i] || !cnt[j] ) continue;
                if ( ( i & j ) == 0 ) {
                    flag = 1; break;
                }
            }
        if ( flag ) printf ( "YES\n" );
        else printf ( "NO\n" );
    }
    return 0;
}

 

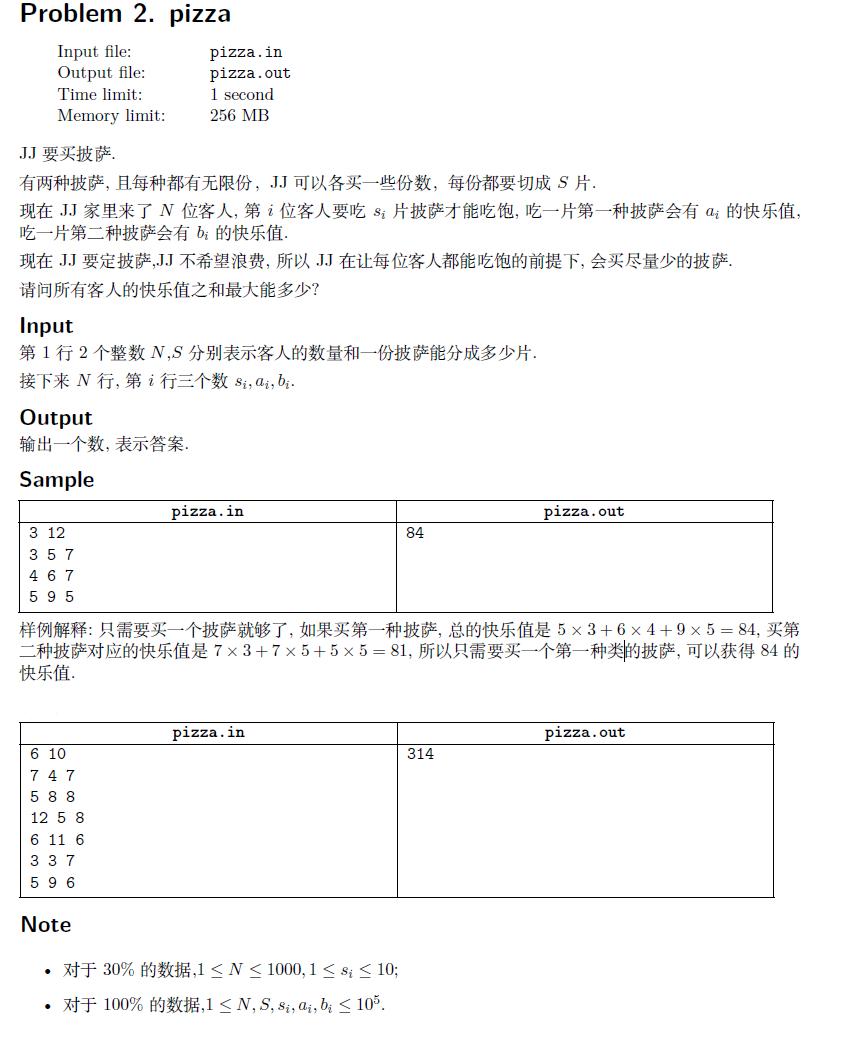
考场上想了好久，觉得这道题是个好复杂的分组背包aaa！！$qwq$，复杂度怎么可能达得到要求！！！

正解贪心...其实正确性还是显然的，因为饼数一定，我们把喜欢吃$a$饼和喜欢$b$饼的人分开，分别按他们的喜欢程度从大到小排序（喜欢程度指$a_i-b_i$或者$b_i-a_i$），我们尽量满足喜欢程度大的人的需求，可是在喜欢$a$和喜欢$b$之间有一个分界线，那里两边的人可能会在$a$和$b$中浮动，可能各选择一部分，因为我们按喜欢程度排的序，就算分界线上的人吃了不太喜欢的那种饼，也是总的快乐值亏得最少的情况。

所以我们先定一个$tot1$，是完全使喜欢$a$饼的全吃到$a$饼，此时可能$b$饼数量不够分给喜欢$b$的人，喜欢$b$中最喜欢$a$的那几个可能被迫吃到$a$，此时是一种情况。另一种则是少给$a$组分配一个，多给$b$组一个，$a$中最喜欢$b$的那几个就会被迫吃到$b$。这两种情况中更优的那个即是答案。可以证明其他情况（多给$a$两个饼少给$b$两个饼）一定会是更劣的，因为这样喜欢吃某种饼的人吃到喜欢的变少了，无用的变多了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;

int n, S, num1, num2;

struct node {
    int a, b, delta;
    ll s;
    node ( ll s = 0, int a = 0, int b = 0, int delta = 0 ) :
        s ( s ), a ( a ), b ( b ), delta ( delta ) { }
} cos1[100005], cos2[100005];
bool cmp ( node a, node b ) { return a.delta > b.delta; }

ll sov ( ll tot1, ll tot2 ) {
    ll s1 = tot1 * S, s2 = tot2 * S;
    ll ans = 0;
    for ( int i = 1; i <= num1; i ++ ) {
        ll qwq = cos1[i].s;
        qwq -= min ( qwq, s1 ); s1 -= min ( s1, cos1[i].s );
        ans += 1ll * cos1[i].a * ( cos1[i].s - qwq );
        if ( qwq ) { ans += 1ll * qwq * cos1[i].b; s2 -= qwq; }
    }
    for ( int i = 1; i <= num2; i ++ ) {
        ll qwq = cos2[i].s;
        qwq -= min ( qwq, s2 ); s2 -= min ( s2, cos2[i].s );
        ans += 1ll * cos2[i].b * ( cos2[i].s - qwq );
        if ( qwq ) { ans += 1ll * qwq * cos2[i].a; s1 -= qwq; }
    }
    return ans;
}

int main ( ) {
    freopen ( "pizza.in", "r", stdin );
    freopen ( "pizza.out", "w", stdout );
    scanf ( "%d%d", &n, &S );
    ll s = 0, sum1 = 0, sum2 = 0;
    for ( int i = 1; i <= n; i ++ ) {
        int s, a, b;
        scanf ( "%d%d%d", &s, &a, &b );
        int delta = a - b;
        if ( delta >= 0 ) sum1 += s, cos1[++num1] = node ( s, a, b, delta );
        else sum2 += s, cos2[++num2] = node ( s, a, b, -delta );
    }
    sort ( cos1 + 1, cos1 + 1 + num1, cmp );
    sort ( cos2 + 1, cos2 + 1 + num2, cmp );
    ll tot = ( sum1 + sum2 + S - 1 ) / S, tot1 = ( sum1 + S - 1 ) / S;
    ll tot2 = tot - tot1;
    ll tmp = sov ( tot1, tot2 );
    if ( tot2 - 1 > 0 ) tmp = max ( tmp, sov ( tot1 + 1, tot2 - 1 ) );
    if ( tot1 - 1 > 0 ) tmp = max ( tmp, sov ( tot1 - 1, tot2 + 1 ) );
    printf ( "%I64d\n", tmp );
    return 0;
}

首先思考暴力做法，定义$dp[i][j]$表示到第$i$个冰淇淋用了$j$个桶时可以得到的最多颜色数。$dp[i][j]=max{dp[k][j-1]+c[k+1][i]}$，$1<=k<=i-1$，其中$c[i][j]$表示从第$i$个冰淇淋到第$j$个的颜色数。

直接暴力枚举复杂度是$O(n^2)$的。考虑如何优化。

可以发现上面的$dp$转移方程中，$j$只会从$j-1$转移得到，我们可以压维。我们把$dp[k][j-1]+c[k+1][i]$看成一个值，问题其实是求一段区间内的最大值。可以用线段树，每个$j$新建一棵线段树，叶子节点储存上述值。

可是线段树怎么更新$c$数组？我们每遍历到一个冰淇淋$i$，因为当前是要把$k+1-i$装到一个桶，$i$影响的实际上是上一个$i$的颜色出现的位置到$i$，这段区间的$c$值需要$+1$，所以我们遍历到$i$时，先更新区间，然后直接查询当前最大的$dp$值即可。复杂度$O(nmlog_n)$。

【注意】因为叶子节点$k$储存的是$dp[k][j-1]+c[k+1][i]$，所以我们要更新$pre[i]+1$到$i$的$c$值，实际上是更新线段树上$pre[i]$到$i-1$这段区间。查询同理。

 

#include<iostream>
#include<cstdio>
using namespace std;

int n, m, pre[20005], las[20005], a[20005];
int dp[20005][2], TR[20005*4], tag[20005*4], now;

void update ( int nd ) {
    TR[nd] = max ( TR[nd<<1], TR[nd<<1|1] );
}

void push_down ( int nd ) {
    if ( tag[nd] ) {
        TR[nd<<1] += tag[nd];
        TR[nd<<1|1] += tag[nd];
        tag[nd<<1] += tag[nd];
        tag[nd<<1|1] += tag[nd];
        tag[nd] = 0;
    }
}

void build ( int nd, int l, int r ) {
    tag[nd] = 0;
    if ( l == r ) {
        TR[nd] = dp[now^1][l];
        return ;
    }
    int mid = ( l + r ) >> 1;
    build ( nd << 1, l, mid );
    build ( nd << 1 | 1, mid + 1, r );
    update ( nd );
}

void add ( int nd, int l, int r, int L, int R, int d ) {
    if ( l >= L && r <= R ) {
        TR[nd] += d;
        tag[nd] += d;
        return ;
    }
    push_down ( nd );
    int mid = ( l + r ) >> 1;
    if ( L <= mid ) add ( nd << 1, l, mid, L, R, d );
    if ( R > mid ) add ( nd << 1 | 1, mid + 1, r, L, R, d );
    update ( nd );
}

int query ( int nd, int l, int r, int L, int R ) {
    if ( l >= L && r <= R ) return TR[nd];
    push_down ( nd );
    int mid = ( l + r ) >> 1, ans = 0;
    if ( L <= mid ) ans = max ( ans, query ( nd << 1, l, mid, L, R ) );
    if ( R > mid ) ans = max ( ans, query ( nd << 1 | 1, mid + 1, r, L, R ) );
    return ans;
}

int main ( ) {
    freopen ( "scream.in", "r", stdin );
    freopen ( "scream.out", "w", stdout );
    scanf ( "%d%d", &n, &m );
    for ( int i = 1; i <= n; i ++ ) {
        scanf ( "%d", &a[i] );
        pre[i] = las[a[i]];
        las[a[i]] = i;
    }
    for ( int i = 1; i <= n; i ++ ) dp[now][i] = dp[now][i-1] + ( pre[i] == 0 );
    for ( int j = 2; j <= m; j ++ ) {
        now ^= 1;
        build ( 1, 1, n );
        for ( int i = 1; i <= n; i ++ ) {
            if ( i < j ) dp[now][i] = 0;
            else {
                add ( 1, 1, n, max ( pre[i], 1 ), i-1, 1 );
                dp[now][i] = query ( 1, 1, n, 1, i-1 );
            }
        }
    }
    printf ( "%d", dp[now][n] );
    return 0;
}