常用排序方法总结
常用排序方法总结
1、插入排序
1.1直接插入排序
算法思想
插入排序的基本方法是:每步将一个待排序的记录按其关键字的大小插到前面已经排序的序列中的适当位置,直到全部记录插入完毕为止。即每次从无序表中取出第一个元素,把它插入到有序表的合适位置,使有序表仍然有序。




代码
public static void InsertSort(int[] array)
{
for(int i=1;i<array.length;i++)
{
if(array[i]<array[i-1])
{
int temp = array[i];
int j=0;
for(j=i-1;j>=0&&temp<array[j];j--)
{
array[j+1]=array[j];
}
array[j+1]=temp;
}
}
}
1.2折半插入排序
算法思想
折半插入排序的基本思想是:顺序地把待排序的序列中的各个元素按其关键字的大小,通过折半查找插入到已排序的序列的适当位置。
代码
void binary_insertion_sort(int arr[],int len)
{
int i,j,temp,m,low,high;
for(i=1;i<len;i++)
{
temp = arr[i];
low=0;
high=i-1;
while(low <= high)
{
m=(low+high)/2;
if(arr[m]>temp)
high=m-1;
else
low=m+1;
}
}
for(j=i-1;j>=high+1;j--)
arr[j+1] = arr[j];
arr[j+1] = temp;
}
2、交换排序
2.1冒泡排序
算法思想
已知一组无序数据a[1]、a[2]、……a[n],需将其按升序排列。首先比较a[1]与a[2]的值,若a[1]大于a[2]则交换两者的值,否则不变。再比较a[2]与a[3]的值,若a[2]大于a[3]则交换两者的值,否则不变。再比较a[3]与a[4],以此类推,最后比较a[n-1]与a[n]的值。这样处理一轮后,a[n]的值一定是这组数据中最大的。再对a[1]a[n-1]以相同方法处理一轮,则a[n-1]的值一定是a[1]a[n-1]中最大的。再对a[1]~a[n-2]以相同方法处理一轮,以此类推。共处理n-1轮后a[1]、a[2]、……a[n]就以升序排列了。降序排列与升序排列相类似,若a[1]小于a[2]则交换两者的值,否则不变,后面以此类推。 总的来讲,每一轮排序后最大(或最小)的数将移动到数据序列的最后,理论上总共要进行n(n-1)/2次交换。
1.原理:比较两个相邻的元素,将值大的元素交换到右边
2.思路:依次比较相邻的两个数,将比较小的数放在前面,比较大的数放在后面。
(1)第一次比较:首先比较第一和第二个数,将小数放在前面,将大数放在后面。
(2)比较第2和第3个数,将小数 放在前面,大数放在后面。
......
(3)如此继续,知道比较到最后的两个数,将小数放在前面,大数放在后面,重复步骤,直至全部排序完成
(4)在上面一趟比较完成后,最后一个数一定是数组中最大的一个数,所以在比较第二趟的时候,最后一个数是不参加比较的。
(5)在第二趟比较完成后,倒数第二个数也一定是数组中倒数第二大数,所以在第三趟的比较中,最后两个数是不参与比较的。
(6)依次类推,每一趟比较次数减少依次
3.举例:
(1)要排序数组:[10,1,35,61,89,36,55]
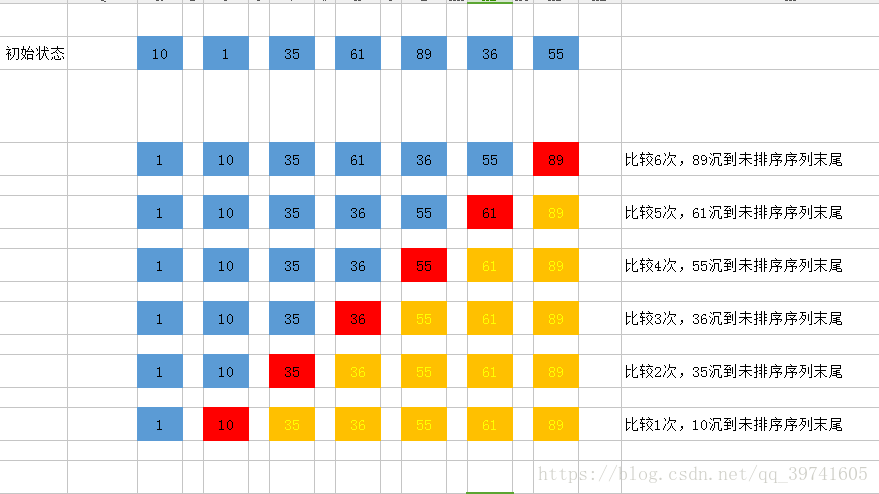
(2)第一趟排序:
第一次排序:10和1比较,10大于1,交换位置 [1,10,35,61,89,36,55]
第二次排序:10和35比较,10小于35,不交换位置 [1,10,35,61,89,36,55]
第三次排序:35和61比较,35小于61,不交换位置 [1,10,35,61,89,36,55]
第四次排序:61和89比较,61小于89,不交换位置 [1,10,35,61,89,36,55]
第五次排序:89和36比较,89大于36,交换位置 [1,10,35,61,36,89,55]
第六次排序:89和55比较,89大于55,交换位置 [1,10,35,61,36,55,89]
第一趟总共进行了六次比较,(1+6=7)排序结果:[1,10,35,61,36,55,89]

(3)第二趟排序:
第一次排序:1和10比较,1小于10,不交换位置 1,10,35,61,36,55,89
第二次排序:10和35比较,10小于35,不交换位置 1,10,35,61,36,55,89
第三次排序:35和61比较,35小于61,不交换位置 1,10,35,61,36,55,89
第四次排序:61和36比较,61大于36,交换位置 1,10,35,36,61,55,89
第五次排序:61和55比较,61大于55,交换位置 1,10,35,36,55,61,89
第二趟总共进行了5次比较,(2+5=7) 排序结果:1,10,35,36,55,61,89
(4)第三趟排序:
第一次排序:1和10比较,1小于10,不交换位置 1,10,35,36,55,61,89
第二次排序:10和35比较,10小于35,不交换位置 1,10,35,36,55,61,89
第三次排序:35和36比较,35小于36,不交换位置 1,10,35,36,55,61,89
第四次排序:36和61比较,36小于61,不交换位置 1,10,35,36,55,61,89
第三趟总共进行了4次比较,(3+4=7) 排序结果:1,10,35,36,55,61,89
到目前位置已经为有序的情形了。
由此可见:N个数字要排序完成,总共进行N-1趟排序,第 i 趟的排序次数为(N-i)次,所以可以用双重循环语句,外层控制循环多少趟,内层控制每一趟的循环次数。
参考链接:https://www.cnblogs.com/bigdata-stone/p/10464243.html
代码
public static void BubbleSort(int[] arr)
{
for(int i=0;i<arr.length-1;i++)
{
for(int j=0;j<arr.length-1-i;j++)
{
if(arr[j]>arr[j+1])
{
int temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=tmp;
}
}
}
}
2.2快速排序
算法思想
设要排序的数组是A[0]……A[N-1],首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它前面,所有比它大的数都放到它后面,这个过程称为一趟快速排序。值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变动。
一趟快速排序的算法是:
1)设置两个变量i、j,排序开始的时候:i=0,j=N-1;
2)以第一个数组元素作为关键数据,赋值给key,即key=A[0];
3)从j开始向前搜索,即由后开始向前搜索(j--),找到第一个小于key的值A[j],将A[j]和A[i]互换;
4)从i开始向后搜索,即由前开始向后搜索(i++),找到第一个大于key的A[i],将A[i]和A[j]互换;
5)重复第3、4步,直到i=j; (3,4步中,没找到符合条件的值,即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值,使得j=j-1,i=i+1,直至找到为止。找到符合条件的值,进行交换的时候i, j指针位置不变。另外,i==j这一过程一定正好是i+或j-完成的时候,此时令循环结束)。
代码
void QuickSort(int arr[],int low,int high)
{ //如果左边索引大于或者等于右边的索引,完成一个组
if(low >= high)
return;
int i=low;
int j=high;
int key = arr[i];
//在当前组查找
while(i<j)
{ //向前遍历,找到小于key的数
while(i<j && arr[j] >= key)
--j;
//小于key的数移到低端
arr[i]=arr[j];
//向后遍历,找到大于key的数
while(i<j && arr[i] <= key)
++i;
//大于key的数移到高端
arr[j]=arr[i];
}
arr[i]=key;
QuickSort(arr,low,i-1);
QuickSort(arr,i+1,high);
}
3、选择排序
3.1简单选择排序
算法思想
在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数中再找最小(或者最大)的与第2个位置的数交换,以此类推,知道第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。即操作方法:
第一趟:从n个记录中找出关键码最小的记录和第一个记录交换;
第二趟:从第二个记录开始的n-1个记录中再选出关键码最小的记录与第二个记录交换
以此类推......
第i趟,则从第i个记录开始的n-i+1个记录中选出关键码最小的记录与第i个记录交换,直到整个序列按关键码有序。
代码
public static void SimpleSelectSort(int[] arry)
{
int tmp = 0;
int t = 0;//最小数标记
for (int i = 0; i < arry.Length; i++)
{
t = i;
for (int j = i + 1; j < arry.Length; j++)
{
if (arry[t] > arry[j])
{
t = j;
}
}
tmp = arry[i];
arry[i] = arry[t];
arry[t] = tmp;
}
}
4、归并排序
4.1 2-路归并排序
算法思想
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
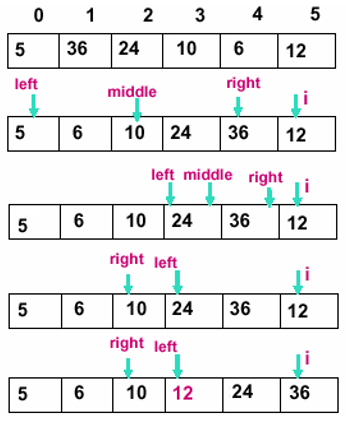
归并过程为:比较a[i]和a[j]的大小,若a[i]≤a[j],则将第一个有序表中的元素a[i]复制到r[k]中,并令i和k分别加上1;否则将第二个有序表中的元素a[j]复制到r[k]中,并令j和k分别加上1,如此循环下去,直到其中一个有序表取完,然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。归并排序的算法我们通常用递归实现,先把待排序区间[s,t]以中点二分,接着把左边子区间排序,再把右边子区间排序,最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。
归并操作(merge),也叫归并算法,指的是将两个顺序序列合并成一个顺序序列的方法。
如 设有数列{6,202,100,301,38,8,1}
初始状态:6,202,100,301,38,8,1
第一次归并后:{6,202},{100,301},{8,38},{1},比较次数:3;
第二次归并后:{6,100,202,301},{1,8,38},比较次数:4;
第三次归并后:{1,6,8,38,100,202,301},比较次数:4;
代码
void Merge(int a[],int low,int mid,int high);
void MergeSort(int a[],int low,int high);
//将两个非降序序列low--mid,mid+1--high合并为一个新的非降序序列
void Merge(int a[],int low,int mid,int high)
{
int len = high-low+1;
int *temp = new int[len];
int i = low,j = mid+1; //i,j分别为两个子序列的游标
int k = 0; //为新合并序列的游标
while(i<=mid && j<=high){
if(a[i]<=a[j]){
temp[k] = a[i];
k++;
i++;
}else{
temp[k] = a[j];
k++;
j++;
}
}
while(i<=mid){ //若第一个子序列有剩余,则直接接到尾部
temp[k] = a[i];
k++;
i++;
}
while(j<=high){ //若第二个子序列有剩余,则直接接到尾部
temp[k] = a[j];
k++;
j++;
}
//copy到a[]
for(k=0;k<len;k++)
a[low+k] = temp[k];
}
//low high为待排序列左右边界
void MergeSort(int a[],int low,int high)
{
if(low<high){
int mid = (low+high)/2;
//递归的划分左右两个子序列
MergeSort(a,low,mid);
MergeSort(a,mid+1,high);
//合并
Merge(a,low,mid,high);
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号