第三十课双向链表的实现 - 周伯通789

公告

第三十课双向链表的实现

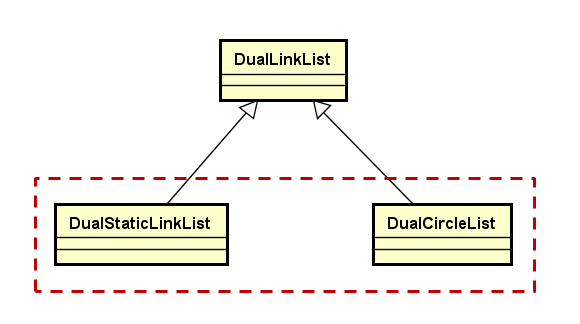
由上图可以看出来，插入和遍历的时间复杂度是不一样的。

这样不管游标在哪一个位置上，都可以通过后继或者前驱指针任意访问。

双向链表的继承层次：

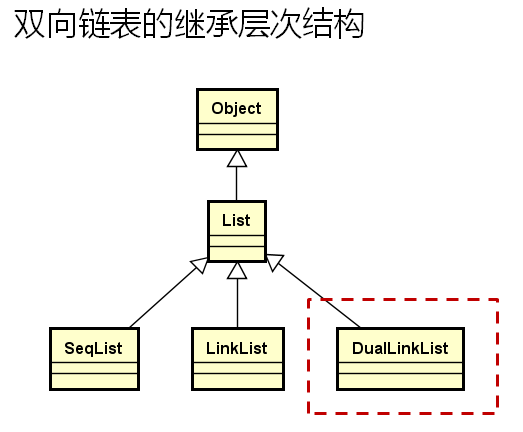
单链表和双向链表应该是兄弟关系，而不应该是继承关系，因为它们的内部机制是完全不同的了。

插入新节点图解：

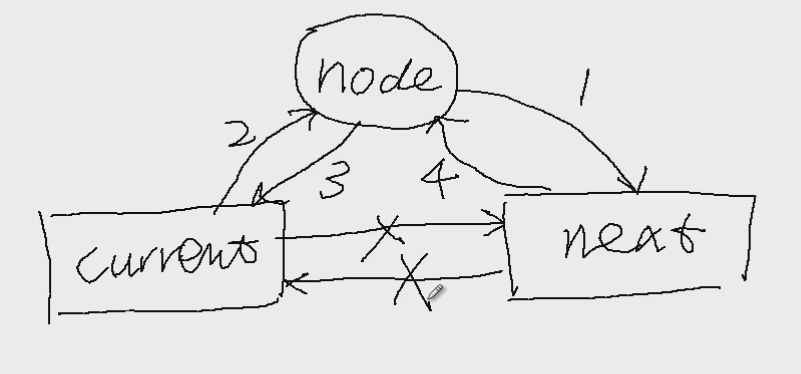
删除节点的步骤：

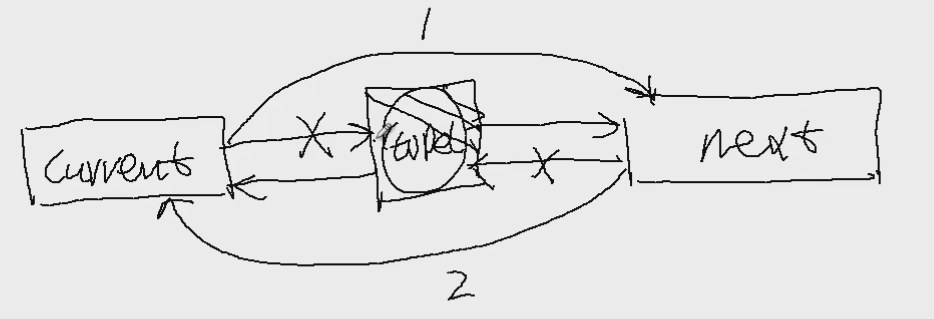
添加DualLinkList.h文件：

  1 #ifndef DUALLINKLIST_H
  2 #define DUALLINKLIST_H
  3 
  4 #include "List.h"
  5 #include "Exception.h"
  6 
  7 namespace DTLib
  8 {
  9 
 10 template < typename T >
 11 class DualLinkList : public List<T>
 12 {
 13 protected:
 14     struct Node : public Object
 15     {
 16         T value;
 17         Node* next;
 18         Node* pre;
 19     };
 20 
 21     mutable struct : public Object
 22     {
 23         char reserved[sizeof(T)];
 24         Node* next;
 25         Node* pre;
 26     }m_header;
 27 
 28     int m_length;
 29     int m_step;
 30     Node* m_current;
 31 
 32     Node* position(int i) const    //  O(n)
 33     {
 34         Node* ret = reinterpret_cast<Node*>(&m_header);
 35 
 36         for(int p = 0; p < i; p++)
 37         {
 38             ret = ret->next;
 39         }
 40 
 41         return ret;
 42     }
 43 
 44     virtual Node* create()
 45     {
 46         return new Node();
 47     }
 48 
 49     virtual void destroy(Node* pn)
 50     {
 51         delete pn;
 52     }
 53 
 54 public:
 55     DualLinkList()
 56     {
 57         m_header.next = NULL;
 58         m_header.pre = NULL;
 59         m_length = 0;
 60         m_step = 1;
 61         m_current = NULL;
 62     }
 63 
 64     bool insert(const T& e)
 65     {
 66         return insert(m_length, e);
 67     }
 68 
 69     bool insert(int i, const T& e)   // O(n)
 70     {
 71         bool ret = ((0 <= i) && (i <= m_length));
 72 
 73         if( ret )
 74         {
 75             Node* node = create();
 76 
 77             if( node != NULL )
 78             {
 79                 Node* current = position(i);
 80                 Node* next = current->next; //即将插入的节点的后继节点
 81 
 82                 node->value = e;
 83 
 84                 node->next = next;  //第1步
 85                 current->next = node; //第2步
 86 
 87                 if( current != reinterpret_cast<Node*>(&m_header))  //判断是否是头结点
 88                 {
 89                     node->pre = current;  // 第3步
 90                 }
 91                 else
 92                 {
 93                     node->pre = NULL;
 94                 }
 95 
 96                 if( next != NULL )
 97                 {
 98                     next->pre = node;   //第4步
 99                 }
100 
101                 m_length++;
102             }
103             else
104             {
105                 THROW_EXCEPTION(NoEnoughMemoryException, "No memery to insert new element...");
106             }
107         }
108 
109         return ret;
110     }
111 
112     bool remove(int i)   // O(n)
113     {
114         bool ret = ((0 <= i) && (i < m_length));
115 
116         if( ret )
117         {
118             Node* current = position(i);
119             Node* toDel = current->next;
120             Node* next = toDel->next;
121 
122             if( m_current == toDel )
123             {
124                 m_current = next;
125             }
126 
127             current->next = next;  //第1步
128 
129             if( next != NULL )
130             {
131                 next->pre = toDel->pre;  //第2步
132             }
133 
134             m_length--;
135 
136             destroy(toDel);
137 
138         }
139 
140         return ret;
141     }
142 
143     bool set(int i, const T& e)   //  O(n)
144     {
145         bool ret = ((0 <= i) && (i < m_length));
146 
147         if( ret )
148         {
149             position(i)->next->value = e;
150         }
151 
152         return ret;
153     }
154 
155     virtual T get(int i) const   // O(n)
156     {
157         T ret;
158 
159         if( get(i, ret) )
160         {
161             return ret;
162         }
163         else
164         {
165             THROW_EXCEPTION(IndexOutOfBoundsException, "Invalid parameter i to get element ...");
166         }
167 
168         return ret;
169     }
170 
171     bool get(int i, T& e) const    // O(n)
172     {
173         bool ret = ((0 <= i) && (i < m_length));
174 
175         if( ret )
176         {
177             e = position(i)->next->value;
178         }
179 
180         return ret;
181     }
182 
183     int find(const T& e) const    //  O(n)
184     {
185         int ret = -1;
186         int i = 0;
187 
188         Node* node = m_header.next;
189 
190         while( node )
191         {
192             if( node->value == e )
193             {
194                 ret = i;
195                 break;
196             }
197             else
198             {
199                 node = node->next;
200                 i++;
201             }
202         }
203 
204         return ret;
205     }
206 
207     int length() const   // O(1)
208     {
209         return m_length;
210     }
211 
212     void clear()    //  O(n)
213     {
214         while( m_length > 0 )
215         {
216             remove(0);
217         }
218     }
219 
220     virtual bool move(int i, int step = 1)
221     {
222         bool ret = (0 <= i) && (i < m_length) && (step > 0);
223 
224         if( ret )
225         {
226             m_current = position(i)->next;
227             m_step = step;
228         }
229 
230         return ret;
231     }
232 
233     virtual bool end()
234     {
235         return (m_current == NULL);
236     }
237 
238     virtual T current()
239     {
240         if( !end() )
241         {
242             return m_current->value;
243         }
244         else
245         {
246             THROW_EXCEPTION(InvalidOperationException, "No value at current position ...");
247         }
248     }
249 
250     virtual bool next()   //每次移动step步
251     {
252         int i = 0;
253 
254         while((i < m_step) && !end())
255         {
256             m_current = m_current->next;
257             i++;
258         }
259 
260         return (i == m_step);
261     }
262 
263     virtual bool pre()
264     {
265         int i = 0;
266 
267         while((i < m_step) && !end())
268         {
269             m_current = m_current->pre;
270             i++;
271         }
272 
273         return (i == m_step);
274     }
275 
276     ~DualLinkList()   //  O(n)
277     {
278         clear();
279     }
280 };
281 
282 }
283 
284 #endif // DUALLINKLIST_H

和LinkList的不同只在于Node的元素，我们新添加了pre成员。

insert函数和remove函数是改动最大的。

新增加了pre函数。

测试程序如下：

 1 #include <iostream>
 2 #include "DualLinkList.h"
 3 
 4 using namespace std;
 5 using namespace DTLib;
 6 
 7 
 8 int main()
 9 {
10     DualLinkList<int> dl;
11 
12     for(int i = 0; i < 5; i++)
13     {
14         dl.insert(0, i);
15     }
16 
17     for(int i = 0; i < dl.length(); i++)
18     {
19         cout << dl.get(i) << endl;
20     }
21 
22     cout << "begin" << endl;
23 
24     for(dl.move(dl.length() - 1); !dl.end(); dl.pre())
25     {
26         cout << dl.current() << endl;
27     }
28 
29     cout << "end" << endl;
30 
31     return 0;
32 }

第一个for循环时间复杂度是O(n*n)，第二个for循环的时间复杂度是O(n)。

结果如下：

测试程序2：

 1 #include <iostream>
 2 #include "DualLinkList.h"
 3 
 4 using namespace std;
 5 using namespace DTLib;
 6 
 7 
 8 int main()
 9 {
10     DualLinkList<int> dl;
11 
12     for(int i = 0; i < 5; i++)
13     {
14         dl.insert(0, i);
15         dl.insert(0, 5);
16     }
17 
18     for(dl.move(0); !dl.end(); dl.next())
19     {
20         cout << dl.current() << endl;
21     }
22 
23     cout << "begin" << endl;
24 
25     dl.move(dl.length() - 1);
26 
27     while(!dl.end())
28     {
29         if( dl.current() == 5 )
30         {
31             cout << dl.current() << endl;
32 
33             dl.remove(dl.find(dl.current()));
34         }
35         else
36         {
37             dl.pre();
38         }
39     }
40 
41     cout << "end" << endl;
42 
43     for(dl.move(0); !dl.end(); dl.next())
44     {
45         cout << dl.current() << endl;
46     }
47 
48     return 0;
49 }

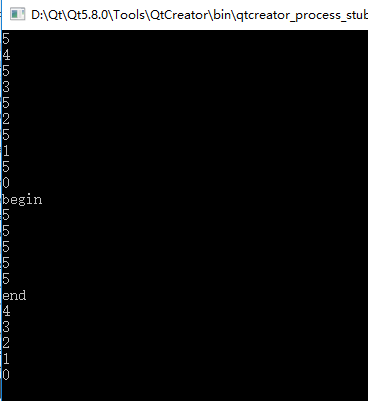
结果如下：

小结：

双向链表的子类：

posted on 2018-09-16 11:14 周伯通789 阅读(291) 评论(0) 编辑收藏举报

刷新页面返回顶部