二叉树的遍历核心思想是:
递归,和各个节点遍历的顺序
根据递归思想,在每个子树中根据根节点访问的顺序可以分为:先根遍历;中根遍历;和后根遍历;左子树和右子树的访问顺序始终不变,都是先左子树再右子树
先根遍历:先访问二叉树的根,再访问访问二叉树的左子树(注意不是左儿子节点,因为遍历是个地推的过程),再访问二叉树的右子树。对二叉树的左右子树也是先根遍历
中根遍历:先访问二叉树的左子树,再访问访问二叉树的根,最后访问二叉树的根。对二叉树的左右子树也是中根遍历
后根遍历:先访问二叉树的左子树,再访问访问二叉树的右子树,再访问二叉树的根。对二叉树的左右子树也是后根遍历
三种遍历的共同点:
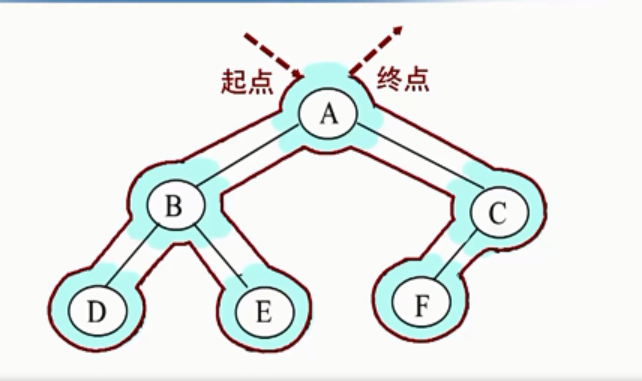
如图所示,按照外围的路径按顺序访问
1,左侧对应先根遍历。即第一次遇到就访问
2.正下方对应中根遍历。即第二次遇到就访问
3.右侧对应后根遍历。即第三次遇到就访问
二叉树的构造(也是使用递归思想,但是这里的递归是指:根节点的左儿子又是该子树的根,根节点的右儿子也是另一个子树的根节点。递归是值根节点概念的递归)
同一个前序序列或者中序序列或者后序序列可能对应不同的二叉树结构。也就是说只有一个前序序列或者中序序列或者后序序列不能够唯一确定一棵树
那么有俩个序列组合起来是否可以唯一确定一棵树?
由前序和后序序列的组合不能唯一确定一棵树
由前序和中序或者中序和后序的组合可以确定一棵树:因为能先确定根,再确定该根的左右子树,递归下去

 posted on
posted on
