04_朴素贝叶斯算法
今天是2020年2月4日星期二,全国确诊人数达到了20471例,确诊人数从一万例到两万例,只用了三天啊,疫情比想象的严重的多啊。影响程度早早超过了非典,普天盛世之下的堂堂中华,也会爆出如此疫情,人类还是弱小,微生物才是地球的主宰啊。
看了一下朴素贝叶斯算法,这次的深入学习,发现了许多之前学习忽略的地方,在这里先简单叙述下感想。看了很多资料讲朴素贝叶斯是生成模型,那就有必要和判别模型做一下对比,通常说判别模型,它是通过“输入特征x”直接学习“输出y”,也就是直接学习输出y和特征x之间的映射关系。比如说判断来诊人员A是否需要输液,k近邻算法仅仅根据来诊人员A的输入特征和哪几个最近邻节点的特征相似,直接多数表决判断A的类别是否需要输液。(这里用k近邻算法作为例子,有点不妥,因为k近邻没有显式的学习过程,决策树章节再分析这个问题)。
朴素贝叶斯作为生成模型的代表,需要先找到输入特征x与输出y的联合概率分布,也就是生成一对数据(x,y)的方式。再计算y在输入特征x的条件下的出现概率,比较不同类别y的大小,哪个类别的y大,未知数据就属于哪个类别。这里首先要解决联合概率分布是什么,接下来是条件分布,最后执果索因是什么,也就是怎样理解结果对原因产生影响,解决了这三个问题,相信就能够对生成模型,有一个大概的了解。
在正式开始吃李航老师的书本内容前,先解决一下概率知识上的盲点。这部分内容仅作参考,因为概率课是水过的…数学二也没有考概率,只是在学习机器学习前简单看了下概率…
我们用P(A)记为事件A发生的概率,P(A∩B)记为事件A和事件B同时发生的概率,称为联合概率,P(A|B)记为在事件B发生的前提下,事件A发生的条件概率。这里的事件A和B不一定具有因果或者先后序列关系。通常我们在描述某个事件发生的概率的时候,其实总是默认了该事件所在的样本空间,现在我们需要重新理解一下这个概念,样本空间是一个实验或随机试验所有可能结果的集合(样本空间的任何一个子集都被称为一个事件)。我们说P(A)是事件A发生的概率,不能离开事件A所处的样本空间,如维恩图中蓝色框部分,事件A的概率P(A)其实是指在样本空间Ω中,事件A部分占样本空间Ω的比率。
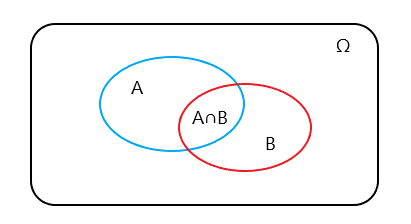
在样本空间Ω下,事件A和事件B同时发生的联合概率P(A∩B)也就是图中A∩B部分占样本空间Ω的比率。来看一下条件概率P(A|B),也就是在事件B发生的前提下,事件A发生的概率,P(A|B)与P(A)的区别在哪里?很明显,是条件事件B。在维恩图中怎么理解呢?前文提到了样本空间,这里的重点就在于样本空间的变化。在P(A)中,指的是A部分占样本空间Ω的比率;在P(A|B)中,有了一个前提,需要事件B先发生,也就是排除了原来样本空间Ω中B部分以外的区域。换句话说,条件的存在意味着样本空间的缩小,那么P(A|B)也就是A∩B部分(事件A、B同时发生,包含了事件A发生)占新的样本空间B的比率。P(A)与P(A|B),除了样本空间的变化,是否存在定量关系呢?这里我们用公式看一下比率关系,用sizeA表示维恩图中A所在部分。

可以得到:
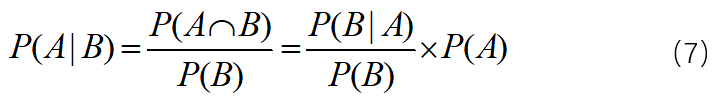
哎,这就有意思了。通过公式的定量表示,我们可以看到事件A在附加了条件下,也就是样本空间缩小的情况下,P(A)与P(A|B)存在一种定量关系。这里大胆的把这个定量关系作为附加条件B之后的调整因子。其实这就是贝叶斯公式,只是换了一个角度进行理解,一千个读者一千个哈姆雷特。
在贝叶斯公式中,P(A)称为先验概率,P(A|B)称为后验概率。我的理解是这样,先验概率P(A)是在事件B发生之前,对A事件的一个判断,一般来说是我们对数据所在领域的历史经验或者常识,这个经验或者常识对该事件发生的概率难以量化,但我们可以对它进行假设;后验概率P(A|B),是事件B发生之后,对事件A发生概率的重新评估。后验概率也就可以理解成:后验概率=先验概率×调整因子,通过调整因子,让预估概率更接近真实概率。
写到这里,大概可以对联合概率、条件概率、贝叶斯公式有个简单的理解了,但是好像还没有扯到生成模型什么事,这就来扯一扯。
在我的理解里,该算法需要抛弃判别模型中的“映射”思路。就是说要理解素朴贝叶斯算法,需要先丢掉“给出一个什么样的输入特征向量x,模型可以得到什么样的输出结果y”这个直接判别的映射想法。说朴素贝叶斯算法是生成模型,实际上就是在判断新的输入实例x具体类别时,要通过训练数据集中(x,y1)、(x,y2)这种具体组合在数据集中出现的概率,结合条件概率再去判断x的类别是y1,还是y2的哪种可能性大。在上边的一堆公式中,可以看到贝叶斯公式(7)的得来,依赖于公式(3)中的事件A和事件B同时出现的联合概率。换句话说,我们要判断新的输入实例x的类别,数据集中的类别分别为y1、y2,类别y有自己的分布规律。例如服从P(y1)=0.8、P(y2)=0.2的二项分布,简单来说,我们看到是y1的概率这么大,直接把x的类别判断为y1就是了。但贝叶斯不是这么做的,因为每个实例x是不一样的(实例x可能的情况有自己的分布)。我们是不是可以根据x在已经确定的情况下,再去判断类别y的条件概率呢?这就意味着样本空间的缩小,在有条件的情况下,再去判断y的类别,肯定要比什么都不知道的情况做判断要准确。也就是我们要找到x,y各个单独事件的组合事件(x,y1)、(x,y2)在数据集中的分布,用来调整类别y的先验概率,得到有条件下的后验结果。
GitHub:https://github.com/wangzycloud/statistical-learning-method
朴素贝叶斯算法
引入
前边说了一大堆乱七八糟的东西,形式化来讲,朴素贝叶斯算法是基于贝叶斯定理和特征条件假设的分类方法。对于给定的训练数据集,首先是利用特征条件独立假设,学习输入输出的联合概率分布。然后基于该模型,对给定的输入实例x,利用贝叶斯定理求出后验概率最大的输出类别y。本节有不少耐看的公式,第一次耐心看懂,之后就没这么晦涩了,接下来按照书中的顺序记录一下,包括朴素贝叶斯法的基本方法、后验概率最大化的含义、参数估计和朴素贝叶斯算法。
基本方法
首先是模型输入、输出情况的说明,输入数据用n维特征向量表示,这里注意一下训练数据集T,数据集T内的数据是由是由事件x,y同时发生的联合概率分布产生。



实际上,学习到了联合概率分布P(X,Y),也就是学习到了生成一个数据(xn+1,yn+1)的方式,这就要我们把输入实例xn+1和相应输出类别yn+1当成一个整体来对待。接下来看一下条件概率分布,我们知道输入特征向量不是一个单独的数值,而是一系列特征分量构成的向量,并且每个分量有不同的取值范围,公式(4.2)反映了这一事实,这就影响到我们对联合概率的求解。每个分量有不同的取值,不同取值的x与类别y构成同时发生的联合事件,各个分量的排列组合结果是一个非常大的数字,直接根据样本出现的频率来估计参数是一个非常困难的事情。假如样本的n个属性都是二值的,则样本空间将有2的n次方种可能的取值,在现实中,这个种类数往往大于训练样本,一些可能的取值在训练集中并不会出现。

这里我们看一下条件独立性假设,实际上就是说,我们强行认为特征向量x的各个分量之间是独立的,相互之间不能有影响,就算有影响,我们也不考虑进来。也就是假设每个分量属性独立的对分类结果产生影响,这是一个很强的假设,通过这个假设,参数求解变得可行,这也是朴素贝叶斯“朴素”的由来。其中,需要估计的参数数量大大减少:
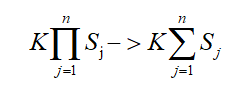
由此,我们可以将各个分量看作生成数据的不同阶段,应用乘法公式得到公式(4.3),也就是各独立变量的联合分布=各独立变量先验概率的乘积。文中提到的条件独立性这一假设,使得朴素贝叶斯法变得简单,但会牺牲一定的分类准确性。


在有了联合概率、条件概率、独立性假设的前提下,在应用公式(4.4)-公式(4.6)后,可以得到最终的朴素贝叶斯分类器,即公式(4.7)。
后验概率最大化
该部分从期望风险最小化的角度,阐述朴素贝叶斯的原理,也就是为什么输出y的分类要取后验概率最大的类。这里存疑,开学后搞起~已找到合适资料,到实验室整理出来就好了。

朴素贝叶斯法的参数估计
先验概率P(Y)表示了样本空间中事件Y各个类别所占的比例,根据大数定律,当训练集包含足够多的样本时,P(Y)可以通过各事件出现的频率来估计。

对于各独立变量的条件概率参数,也是通过极大似然估计得出。

贝叶斯算法


算法流程图:

贝叶斯估计
通过极大似然估计法,我们计算出了该数据集内输入特征x各个属性独立性假设下的条件概率。而如果待预测实例的某个属性值没有在训练集中出现过,根据公式(4.9)计算条件概率就会出现概率值为0的情况。无论该实例的属性如何,根据连乘公式,最终的类别概率都为0,无法做出判断。针对这种情况怎么避免呢?对分母分子进行修正,这就是贝叶斯估计(实际上就是分子分母同时加上一个常数,避免0的情况)。

理解贝叶斯的一个小例子
医院里出现了一例尚未确诊的肺炎患者(疑似状态),猜测他被感染的原因可能是:
(1) 华南海鲜市场吃过海鲜
(2) 去武汉旅行刚回来
(3) 同其它患者密切接触过
根据其它人的确诊结果,我们知道如果去海鲜市场吃过海鲜,有70%几率会确诊;去武汉旅行的人有60%的几率确诊;同其它患者密切接触过的话,有50%的几率确诊。现在他昏迷了,根据他体温及肺部CT病症严重程度,猜测这三种原因的可能性概率分别为50%、30%、20%。那么,如果现在核酸试剂结果为阳性,被确诊了。在已知确诊的条件下,考虑是哪种原因造成了感染?

由全概率公式,我们可以得到确诊、疑似的概率分别是:
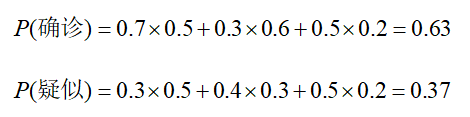
由贝叶斯公式,在确诊的条件下,三种可能性的大小被调整为:

在已经确诊的条件下,比较三者的后验概率,可以得到该患者因吃海鲜被感染的可能性最大。执果索因,简单讲就是将结果考虑到发生原因的评估上,对前期评估进行调整。
代码效果




 浙公网安备 33010602011771号
浙公网安备 33010602011771号