【自然语言处理（二）】条件随机场 CRF

判别式模型与生成式模型

已知的机器学习模型中，分成了生成式模型和判别式模型两大类型。朴素贝叶斯、贝叶斯网络、pLSA、LDA等模型都是先对联合概率分布进行建模，然后再通过计算边缘分布得到对变量的预测，所以它们都属于生成式模型。

其他的还有HMM模型。

相比生成式模型，判别式模型家族更加庞大一些，包括感知机（单层神经网络）、条件随机场、支持向量机、神经网络。而所谓的神经网络深度学习,也不过是判别式家族成员之一而已。判别式模型并不介意输出的到底是[0,1]区间内的概率p(ylx)，还是一个分值score(x,y)，只保证概率越大分值越大即可。万一下游应用需要概率，只需将分值传入softmax函数转换一下即可:

 

 

 

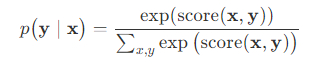
为了分析多维随机变量分布，人们使用了概率图模型这个强大的工具。

概率图模型

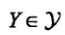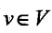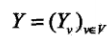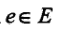概率图模型（probabilistic graphical model）是由图表示的概率分布．设有联合概率分布P(Y)，是一组随机变量．由无向图G=(V,E)表示概率分布P(Y)，即在图G中，结点表示一个随机变量Y，﹔边表示随机变量之间的概率依赖关系。[1]

PGM大致可以分为两种，directed graphical model(又称贝叶斯网络）和undirected graphical model（又称马尔可夫随机场）。

在概率有向图中，每个事件之间的方向代表因果关系。边的权重正是一个条件概率。

无向图模型则不探究每个事件的因果关系，也就是说不涉及条件概率分解。无向图模型的边没有方向，仅仅代表两个事件有关联，不表示谁是因谁是果。

而在无向图中，无向边表示两个变量的一种互相关系，互相影响，互相软限制等等，不再是条件概率。

概率图模型分类

如下图：在概率模型中，有向图按照单源点、链到有向图的方式划分，分别是朴素贝叶斯、HMM、贝叶斯网络；

如果加入条件概率，则分别是逻辑回归，链条条件随机场，一般条件随机场。

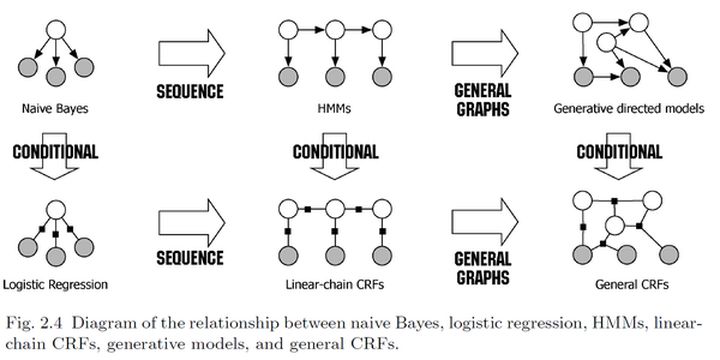
图中，逻辑回归是从属于判别模型、最大熵模型，对P(y|x)建模。我们可以看到深色的圆都是观测的状态，而白色的圆是隐含的状态。

无向图模型将多维随机变量的联合分布分解为一系列最大团中的因子之积，称为概率无向图的因子分解，其联合分布如下：

其中C为最大团的集合，Q为某个最大团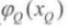；可以是指数函数

 

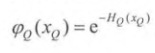
而 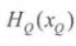 为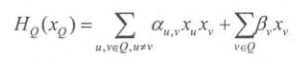 

 

 

而

CRF在最大熵马尔可夫模型的基础 上， 进行了全局归一化。Z是归一化因子，枚举了整个隐状态序列x的所有可能。

 

本文采用记号

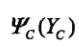表示势函数，必须为正；一般定义为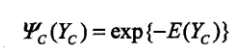其中Y_C表示C对应的随机变量；

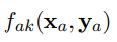特征函数，仅在xa,ya为指定值时为1，其余情况=0

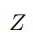规范化因子，也称分配函数（partition function），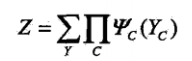

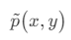经验分布函数，即训练集上x，y的取值概率

条件随机场

条件随机场(Conditional Random Field，CRF )是一种给定输入随机变量x，求解条件概率p(y|x)的概率无向图模型。

定义：

设X与Y是随机变量，P(Y|X)是在给定X的条件下Y的条件概率分布．若随机变量Y构成一个由无向图G=(V,E)表示的马尔可夫随机场，即

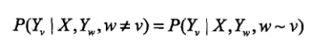
则称该无向图表示的模型为条件随机场[1]。

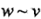表示G中v的所有相邻点

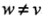表示v以外的所有结点

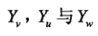表示v，u，w对应的随机变量

线性链条件随机场

CRF用于序列标注时，特例化为线性链条件随机场（linear-chain CRF）。

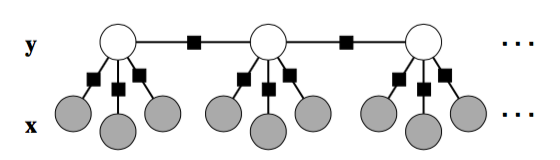
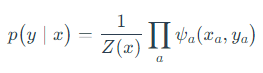
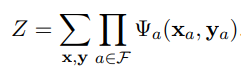
线性链条件随机场的训练

下面我们来推导线性条件随机场的最优化。

如果将所有特征函数与权重分别写作向量形式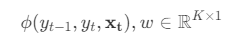,则线性链条件随机场的定义可以简化为：

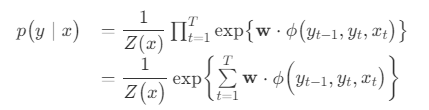
其中Z

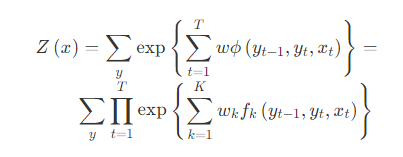(1)

对数似然函数

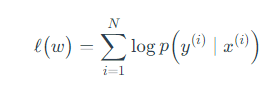
将式(1)代入上式，似然函数展开为:

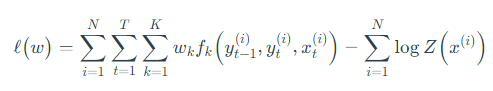
正则化函数

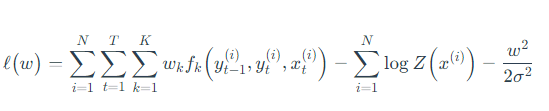
求偏导

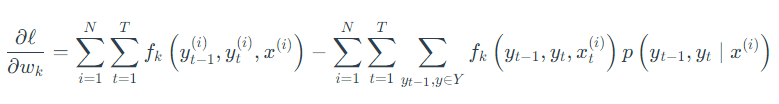
特征函数的经验分布就是特征函数在训练集上的计数统计

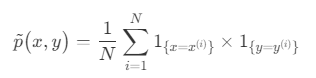
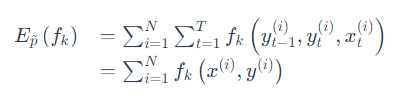
第二项：

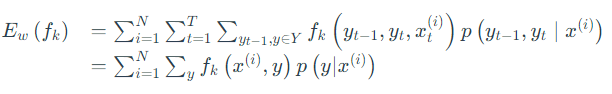
综上简化为：

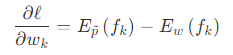
由于条件随机场的对数似然函数为凸函数( concave function )，所以可以利用许多凸优化算法。其中之一即为L-BFGS凸优化算法。

L-BFGS凸优化算法

 

其中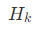是用于降低计算复杂度而经过变换的Hessian矩阵，用以代替Hessian矩阵的逆。

条件随机场与感知机

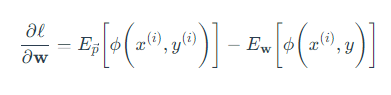
执行梯度上升,让参数点顺着梯度方向移动，得到更新表达式:

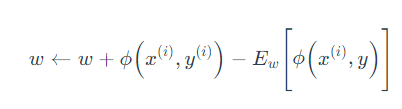
对比感知机的更新表达式

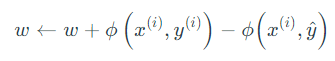
可知每次迭代，CRF会对所有给出错误答案的特征函数进行惩罚，而感知机仅惩罚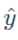的特征函数。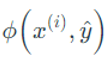

其他

要了解概率图模型的相关知识，可参见：https://ermongroup.github.io/cs228-notes/。

线性CRF的具体计算，可参见https://www.cnblogs.com/pinard/p/7055072.html

CRF的工具包CRF++ https://taku910.github.io/crfpp/

References

[1]统计学习方法 李航

[2]数值优化：理解L-BFGS算法http://www.hankcs.com/ml/l-bfgs.html

[3]无向图(Undirected Graphical Models) https://zhangzhenhu.github.io/blog/probability_model/