【自然语言处理(一)】结构化感知机
感知机
感知机(perceptron)是一种线性分类模型。1957年, 由计算科学家Rosenblatt提出。
从仿生学的角度,一个感知机就是一个神经元。如图所示:
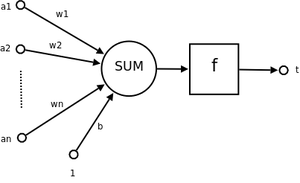
其中a1~an为一个样本的属性值。
在执行线性分类的任务中,它可以对样本输出对应的特征向量。一旦将数据转换为特征向量,那么分类问题即变成对样本空间的分割,此后文本分类问题即与文本解耦,变成一个数学问题。这正是传统机器学习处理文本分类的滥觞。
二维空间中,如果决策边界是直线,则称产生该决策边界的模型为线性分类模型。推广开来,三维空间中的线性模型用平面做决策,任意维度空间中的线性决策边界统称为分离超平面( separating hyperplane )。
决策边界
最简单的感知机,接收N个输入,产生输出。

f(x)为自定义的函数,如:
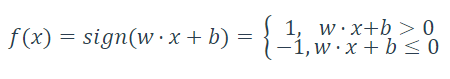
下文均以围绕此f(x)分析。
当y=f(x)=+1,分类为正。
训练感知机模型,即确定模型参数w和b,使之在数据上得到最小化的误差。损失函数一个自然的想法为误分类点到分类超平面的总距离。单个样本点的距离:
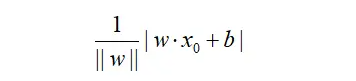
||w||为L2范数。
考虑y的正负,则误分类点的总距离为

这个很自然地联想到SVM的损失函数。确实SVM跟感知机的损失函数是相似的,但是SVM的系数保留了w的分母,而感知机一般舍弃掉分母而不会影响训练结果[1]。
求损失函数的梯度:

对参数的更新:
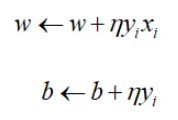
η为学习率。
感知机学习算法
输入:训练数据集T=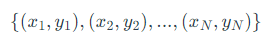 ,x,为实数向量,y,为1或者-1,学习率η(0<η<=1) 。
,x,为实数向量,y,为1或者-1,学习率η(0<η<=1) 。
输出: w, b,即感知机模型。.
(1)选取初值w0,b0;
(2)在训练数据集中选取数据();
(3)如果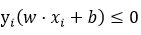 ,则更新w,b:
,则更新w,b:
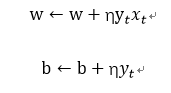
(4)转至(2),直到训练数据集中没有误分类点。
1.1 投票感知机与平均感知机
在训练的过程中,每次迭代都产生一个新模型,不知道哪个更好。一般而言,新模型是更好的,但是并不绝对。此时改进一下,每次迭代的模型都保留,准确率也保留。预测时每个模型都给出自己的结果,乘以它的准确率加权平均值作为最终结果,这样的算法称为投票感知机。显然,如果模型准确度单调上升,则这个结果会弱于保留最新模型的结果。另外,投票感知机要保留多个模型,存储和计算开销较大。
更实际的做法是平均感知机,即在训练时不需要保存多个模型的参数,而是在迭代过程中只保留平均后的模型,最终得到加权平均模型。每当分类出错,就对w_d进行更新。由于大部分训练实例只会引起特定的几个权重变化,即变动参数个数N_w << 总个数N_all,因此没有必要在每次迭代的时候便对所有参数累加,可以根据x(i)_d判断是否需要更新w_d进行优化,因此每个参数的最近更新时间可能是不一样的。对每一个参数w_d,用sum_d和time_d分别表示w_d迭代之和,w_id上次更新时间。
1.2 平均感知机算法
(1)为每个参数w,初始化累计量=0,上次更新时刻=0,当前时刻t =0。
(2) ,读入训练样本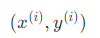 ,执行预测
,执行预测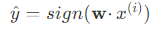 。
。
(3)如果 ,则对所有需更新(即
,则对所有需更新(即 )的w,执行:
)的w,执行:
更新
更新
更新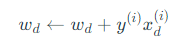
(4)训练指定迭代次数后计算平均值: 
1.3 结构感知机
NLP里的问题包含了分类问题和结构化预测问题。结构化预测的典型例子有序列标注、句法结构分析(输出句法树)、机器翻译结构预测(输出完整译文)。
原始的感知机是用来做分类/回归预测的,而要解决结构化预测问题,感知机需要使用结构化学习过程。需要对感知机学习算法稍加改造,引入打分函数。
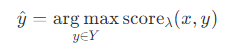
1.4算法
1.4.1 结构化感知机算法
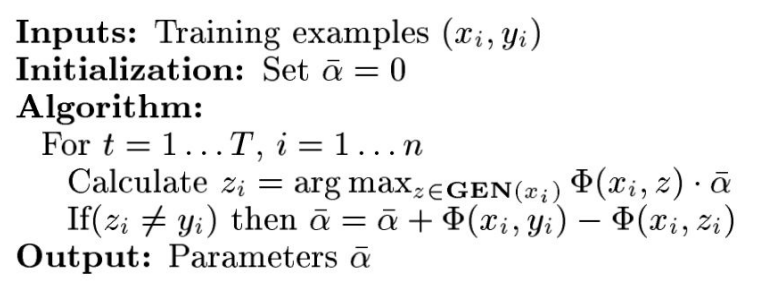
对于其中的 ,可以看到状态预测是根据一个函数的最大值计算得到的,此时需要使用GEN(xi)表示的维特比算法遍历所有可能的z状态。
,可以看到状态预测是根据一个函数的最大值计算得到的,此时需要使用GEN(xi)表示的维特比算法遍历所有可能的z状态。
1.4.2解码的维特比算法
维特比算法之前我们是在隐马尔可夫模型HMM中遇到的。这个算法使用动态规划的思想,用于计算给定符号序列的时候,搜索并确定最大概率的状态序列。这种问题被称为解码问题[2]。
记号
 :d维向量
:d维向量
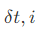 时刻t以si结尾的所有状态路径的最高分数
时刻t以si结尾的所有状态路径的最高分数


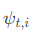 时刻t取得状态si的时候的状态前继,si为已经确定的最大概率状态,由终态的该值可以回溯复原最大概率序列。
时刻t取得状态si的时候的状态前继,si为已经确定的最大概率状态,由终态的该值可以回溯复原最大概率序列。
其中,最大概率以score(x,y)代替,则有:

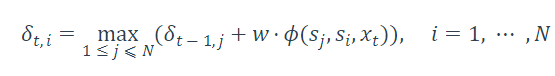
1.初始化
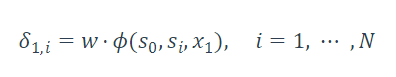
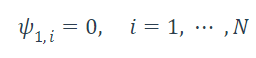
2.在时间t,状态更新

记录前继路径
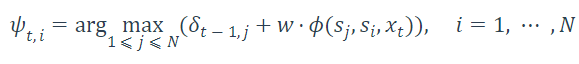
2.时间t=t+1,回到2
4.最后根据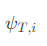 回溯即可得到。
回溯即可得到。
这里唯一的理解难点只是打分函数的设计。对于
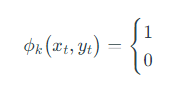
其值何时为1,何时为0,应使得函数在正确样本上取得更高的值,在最完美的结果上取得最大的值。这个取决于实际的问题,例如词性标注中对词性的输入特征通常包括当前词、前一个词和后一个词,以及它们的词性等信息。感知机会根据训练数据逐步调整权重,以使得打分函数对于正确的标记具有更高的得分。
其他
对于OOV(Out of Vocabulary词典外的词汇),基于感知机的在线学习能力,可以对标注样本执行增量训练。用户需要给模型提供一个已经分好词的句子,模型根据这个标签序列重新训练所有样本,更新模型参数。实验结果表明,基于感知机的在线学习能力可以有效应对OOV。
Viterbi算法的实现
public double viterbiDecode(Instance instance, int[] guessLabel) { final int[] allLabel = featureMap.allLabels(); final int bos = featureMap.bosTag(); final int sentenceLength = instance.tagArray.length; final int labelSize = allLabel.length; int[][] preMatrix = new int[sentenceLength][labelSize]; double[][] scoreMatrix = new double[2][labelSize]; for (int i = 0; i < sentenceLength; i++) { int _i = i & 1; int _i_1 = 1 - _i; int[] allFeature = instance.getFeatureAt(i); final int transitionFeatureIndex = allFeature.length - 1; if (0 == i) { allFeature[transitionFeatureIndex] = bos; for (int j = 0; j < allLabel.length; j++) { preMatrix[0][j] = j; double score = score(allFeature, j); scoreMatrix[0][j] = score; } } else { for (int curLabel = 0; curLabel < allLabel.length; curLabel++) { double maxScore = Integer.MIN_VALUE; for (int preLabel = 0; preLabel < allLabel.length; preLabel++) { allFeature[transitionFeatureIndex] = preLabel; double score = score(allFeature, curLabel); double curScore = scoreMatrix[_i_1][preLabel] + score; if (maxScore < curScore) { maxScore = curScore; preMatrix[i][curLabel] = preLabel; scoreMatrix[_i][curLabel] = maxScore; } } } } } int maxIndex = 0; double maxScore = scoreMatrix[(sentenceLength - 1) & 1][0]; for (int index = 1; index < allLabel.length; index++) { if (maxScore < scoreMatrix[(sentenceLength - 1) & 1][index]) { maxIndex = index; maxScore = scoreMatrix[(sentenceLength - 1) & 1][index]; } } for (int i = sentenceLength - 1; i >= 0; --i) { guessLabel[i] = allLabel[maxIndex]; maxIndex = preMatrix[i][maxIndex]; } return maxScore; }
Reference
[1]自然语言处理入门 第五章 何晗


 浙公网安备 33010602011771号
浙公网安备 33010602011771号