字符串经典算法 Knuth-Morris-Pratt Boyer-Moore AC(Aho-Corasick)算法 后缀自动机
常见字符串问题:
闲言少叙,我们直接来解决下面几个问题。
给定字符串s,t,求t在s中匹配的子串位置
给定一个字符串s,求最长回文子串
给定字符串s,t,最长公共连续子串问题
对于问题1,也叫exact matching问题。
朴素的解法是依次从s的起始位置出发,依次比较跟t长度相同的子串,此算法复杂度为O(N*M),空间复杂度为O(M),确切的说是单个t的长度。
对此的解决方法有:
KMP算法: Knuth-Morris-Pratt,最差O(N+M)的复杂度
Boyer-Moore算法: BM算法,最差是线性,可能是次线性的复杂度。
Apostolico-Giancarlo算法: 有BM算法的效率,而且相对简单的证明最差线性复杂度(介绍如此,实际并不)
对于问题2,解决方法有O(N^3)的暴力解法,也有Manacher(马拉车)算法。
对于问题3,解决方法有动态规划,复杂度O(N*M)而且空间复杂度高;最好且最复杂的解法是后缀自动机SAM,复杂度是O(N+M)。
问题1其实是单模式匹配,由此衍生出的多模式匹配问题需要用到AC自动机,而AC自动机也有优劣的实现之分。
参考:
algorithms-on-strings-trees-and-sequences,Cambridge University Press,1997
KMP算法:
应用
Knuth-Morris-Pratt算法,求子串匹配的问题。
leetcode中的题目5正是它的最直接应用;
题目中提到haystack,needle,分别对应文本和模式串,是英语中的"谷堆取针",或大海捞针之义。我们用s、needle表示。
性质
KMP算法通过预处理模式串,记录每个模式串位置下的前驱位置,保存在数组中。
匹配的时候,s、needle往后遍历,字符失配的时候needle根据next数组跳转回上一步;由于原始的KMP算法中用到公共前后缀长度的思路,如果失配返回上一次位置仍然可能进行回退,所以有第二个优化版本如下。s是一直递增的,而needle每次操作不超过1次,所以最大复杂度为O(N)。
if (x[i] == x[j]) kmpNext[i] = kmpNext[j]; else kmpNext[i] = j;
关于跳转的原理,可以见下面的链接。
http://wiki.jikexueyuan.com/project/kmp-algorithm/define.html
代码
void preKmp(string x, vector<int>& kmpNext) { int i, j; int m = x.size(); i = 0; j = kmpNext[0] = -1; while (i < m - 1) { while (j > -1 && x[i] != x[j]) j = kmpNext[j]; i++; j++; if (x[i] == x[j]) kmpNext[i] = kmpNext[j]; else kmpNext[i] = j; } for (int i = 0; i < m; i++) { printf("[%d %d]", i, kmpNext[i]); } printf("\n"); } void KMP(string x, int m, string y, int n) { int i, j; vector<int> kmpNext(m); /* Preprocessing */ preKmp(x, kmpNext); /* Searching */ i = j = 0; while (j < n) { while (i > -1 && x[i] != y[j]) i = kmpNext[i]; i++; j++; if (i >= m) { printf("match %d\n", j - i); i = kmpNext[i]; } } } // void expect_test(string a, string b) { // assert(a == b); // } int main() { string s, pattern; cin >> s >> pattern; clock_t t1 = clock(); KMP(s, s.size(), pattern, pattern.size()); double sec = (clock() - t1) / CLOCKS_PER_SEC; printf("match %.2fs", sec); return 0; }
术语解释
失配:遍历串的时候比较发现两个字符不相等,称为失配;
模式串:如果想判断字符串s中是否包含字符串t,则t称为模式串,而s称为文本串。
文本串:如上
Boyer-Moore算法
概念
好后缀:只要清楚了失配的概念,好后缀是根据模式串后缀的下标移动位数的数组;
坏字符:根据失配的文本串字符得到的移动步数数组。
性质
预处理要开bmBc,bmGs,suffix三个数组,但是只是模式串的,如果模式串可控,在实际中还是可应用的。编辑器的文字匹配常用的算法。
可以参考很多已有的博客。
右移:其实所谓的右移k位,可以是说模式串往左移动k位,为什么看起来是往右移动了呢?因为模式串跳过k位,下一位下标减少了k,而文本串不变,
说明相对的模式串往右移动了。


参考:http://wiki.jikexueyuan.com/project/kmp-algorithm/bm.html
Manacher算法:
Manacher算法用来求最大回文子串。
对字符串做预处理,在每个字符的两边都插入'#',使得字符串长度为奇数(除非是空串,但是可以处理)。该处理的意义是方便每次都有一个中心点,以做左右对称的计算。
思路是遍历字符串,更新最大回文的右边界R和最大的半径、中心点C,在过程中得到最大的半径。当前位置最大半径的更新来自记录的最大半径值,可分两组情况讨论,即左对称点的最大回文范围是否已在大半径内,如果是直接用其更新,否则就扩展到后面直到不匹配;
图1是落在半径内的结果,计算方法为:p[i] = R > i ? min(p[2 * C - i], R - i) : 1;
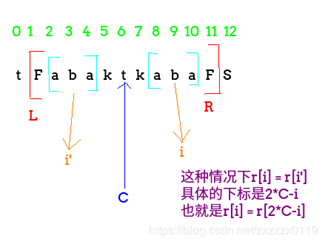
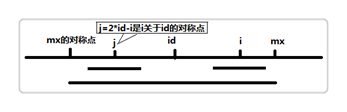
图1 最大回文范围的一种情况
知道p之后可以更新对应的最大字符串。
算法的实现如下:
#include <bits/stdc++.h> using namespace std; int manacher(string& s, vector<int>& segment) { /* 忽略s=""的情况 */ int n = s.size(); string new_s = "#"; for (int i = 0; i < n; i++) { new_s += s[i]; new_s += '#'; } int R = 0, C = 0; int mx = 0; //最大半径 vector<int> p(2 * n + 1); //每个位置为中心的最大回文半径 int len = 2 * n + 1; int cx = -1; for (int i = 0; i < len; i++) { p[i] = R > i ? min(p[2 * C - i], R - i) : 1; while (i - p[i] >= 0 && i + p[i] < len && new_s[i - p[i]] == new_s[i + p[i]]) { p[i]++; } if (i + p[i] > R) { C = i; R = i + p[i]; if (p[i] > mx) { mx = p[i]; cx = C; } } } segment[0] = (cx - mx + 1) / 2; //修改后的串起始位置除以2恢复原位置 segment[1] = mx - 1; printf("%d %d\n", mx, R); return 0; } int main() { string s; while (cin >> s) { vector<int> segment(2); //[起始位置,长度] manacher(s, segment); cout << segment[0] << " " << s.substr(segment[0], segment[1]) << endl; } return 0; }
代码中返回的结果为最大回文子串的第一个结果。
一些细节
1.有实际意义的一般不是求最大长度,所以用segment记录起始位置和长度,以打印子串。
2.处理后的字符串中,像#a#b#b#a#的奇数位为1。
3.空串也可以处理,反正返回0了。
4.插入的结果不要求是字符串中没出现的,只是惯例是插入#。
5.中心点c的左右对称坐标a,b满足a+b=2c,这是几何性质。
上图2用到了以下博客的图:
Manacher 算法,刘毅,https://subetter.com/algorithm/manacher-algorithm.html
AC自动机:
应用
Aho-Corasick: KMP的改良算法,用来进行多模式匹配的。所谓的多模式匹配,是说给定n个模式串pattern,一个文本串,求文本串里匹配了多少个模式串(顺带也可以求出具体串)。
如果你不懂trie树和kmp算法,请先了解相关知识。AC自动机中包含了类似的思想。
实现思路如下:
根据pattern构建一个DFA(如果只考虑实线,它就是一棵trie树),参考下图或其他博客:
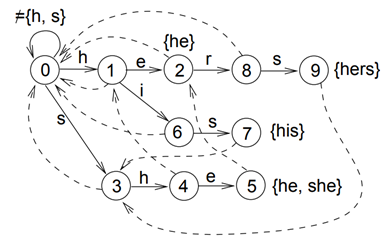
图2 构建的DFA
性质
内部实现经常会提到goto表,failure表,但是这只是个抽象,trie树中没有直接的表,而是存了一些状态转移的数组在结构中;
由于前人之述备矣,这里只是提出几个AC自动机的问题:
1. AC自动机也有naïve方式的实现,例如只处理26个字母的;但是AC自动机如果要实现任意ascii和unicode的转移,不能采用简单的256或65536大小的数组,一般是采用Map<Character, State>,但是空间、时间效率无法同时保证,解决方法看第4点,只要O(1)的时间复杂度和必要的空间复杂度即可进行状态转移;
2.处理过程包括了预处理success转移、output数组、BFS构建failure数组;
3.AC自动机可以跟线段树组合实现文本字符串中所有位置的模式匹配报告;
4.可以参考hankcs网站上的AC自动机、AC自动机的双数组trie、分词器、,其中也参考了一个日本人的实现。利用双数组trie树,可以高效地实现状态转移。
假设现在已经实现了一个AC自动机,其用法如下:
List<String> patterns = {"he", "his", "her", "hers"};
ACTrie trie = new ACTrie();
trie.build(patterns);
String text = "ushers";
res = trie.parseText(text);
双数组trie:
应用
双数组trie是用来压缩Trie空间的。
双数组Trie的一种实现 An Implementation of Double-Array Trie https://www.cnblogs.com/DjangoBlog/p/4072972.html
以上文章阐明了双数组trie树的来历,利用双数组trie树可以用来提供trie树的状态转移功能。其原理是既然有s到t的转换,则以s的地址加字符作为新状态的下标。这个是跟普通的AC自动机生成状态下标的过程不同的。
而check[t]记录了转移到该状态的前一个状态下标。
为什么要用到base数组?可以举一个例子,插入字符编码为'A'和2的数字后我们得到了
base[state('A')] + code[20] = base[state('A' + 20)];这里base[state('A' + 20)]中的下标是个字符串的状态,而base[i]是个int。那么该int值是固定的吗?是的,因为该状态只能从上一个状态string('A')唯一得来。但是反之我们遇到该状态的int值,不一定代表上一个状态就是'A'。
例如若base['B'] = 'A' + 2(该情况是可以满足的),那么base[state('B'.concat(18))] = base[state('B')] + code[18] = base['A'] + code[2 + 18] = base[state('A'.concat(20))]
解决该问题可以额外增加一个check数组,因为每个状态的前继是唯一的。
状态转移如图:
check[base[s] + c] = s
t = base[s] + c
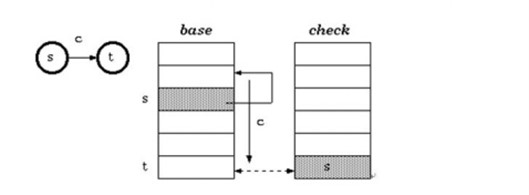
由于要区分初始节点,初始化了base[0] = 1, check[0] = 0,如下所示,这里的状态转移是加c+1而不是c。双数组trie的实现不是唯一的,包括要校验的位置可以不是s而是base[s],但是要保证check[t]位置保存的时候也是base[s]。
protected int transitionWithRoot(int nodePos, char c) { int b = base[nodePos]; int p; p = b + c + 1; if (b != check[p]) { if (nodePos == 0) return 0; return -1; } return p; }
后缀自动机:
应用
后缀数组、后缀自动机可以解决大字符串的LCS问题(小的可以用动态规划和暴力解决)
suffix automata,SAM。为了解决后缀树构造和查询时,时间复杂度和空间复杂度过大的的问题。好了,那为什么要构造后缀树?因为它能解决最长回文、最长公共子串、唯一子串种类等问题。
后缀自动机是一个基于trie的字符串有向图,时间和空间复杂度均为O(N)。
基本概念
后缀自动机一·基本概念 http://hihocoder.com/problemset/problem/1441
构成DFA的五元组 <字符集,状态集,转移函数、起始状态、终结状态集>
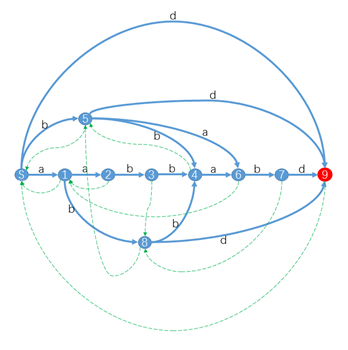
图3 后缀自动机
子串的结束位置集合endpos,即子串在原串中所有出现地方的右端下标;每个DFA状态中包含所有具有相同endpos的子串。
性质1:每个到终点的路径都是原串的后缀,否则不是后缀。
性质2:每个状态可能代表多个子串,而且要用到某个状态中的最长子串,最短子串。
LCS问题
解决LCS问题可以用后缀自动机、后缀树。
以下代码:
struct SAM { SAM *pre,*son[26]; int len,g; } que[N],*root,*tail; int tot; void add(int c,int l) { SAM *p=tail,*np=&que[tot++]; np->len=l; tail=np; while(p&&p->son[c]==NULL) p->son[c]=np,p=p->pre; if(p==NULL) np->pre=root; else { SAM *q=p->son[c]; if(p->len+1==q->len) np->pre=q; else { SAM *nq=&que[tot++]; *nq=*q; nq->len=p->len+1; np->pre=q->pre=nq; while(p&&p->son[c]==q) p->son[c]=nq,p=p->pre; } } } char a[N/2],b[N/2]; int lcs(char a[],char b[]) { memset(que,0,sizeof(que)); tot=0; root=tail=&que[tot++]; for(int i=0; a[i]; i++) add(a[i]-'a',i+1); SAM *p=root; int ans=0; for(int i=0,l=0; b[i]; i++,ans=max(ans,l)) { int c=b[i]-'a'; if(p->son[c]) p=p->son[c],l++; else { while(p&&p->son[c]==NULL) p=p->pre; if(p==NULL) p=root,l=0; else l=p->len+1,p=p->son[c]; } } return ans; }
这里面http://devhui.com/2015/04/21/Longest-Common-Substring/ 抄了Byvoid和陈立杰的。
以上代码存在的问题
显然它就是处理naïve情况下的自动机的,只处理a-z的字符;
不是动态大小的自动机,一开始就占用了空间。
不过都可以解决。
具体原理参考陈立杰的后缀自动机的讲稿。
References:
[1] algorithms-on-strings-trees-and-sequences,Cambridge University Press,1997
[2]EXACT STRING MATCHING ALGORITHMS (KMP, BM) http://www-igm.univ-mlv.fr/~lecroq/string/index.html
[3] Manacher 算法,刘毅,https://subetter.com/algorithm/manacher-algorithm.html
[4] http://devhui.com/2015/04/21/Longest-Common-Substring/
[5] AC自动机模板(【洛谷3808】),
小蒟蒻yyb ,https://blog.csdn.net/qq_30974369/article/details/74557224
[6] Aho Corasick自动机结合DoubleArrayTrie极速多模式匹配,hankcs(何晗),
http://www.hankcs.com/program/algorithm/aho-corasick-double-array-trie.html
[7] 后缀自动机一·基本概念 http://hihocoder.com/problemset/problem/1441



 浙公网安备 33010602011771号
浙公网安备 33010602011771号