数据结构和算法
数据结构和算法
数据结构
数据结构始计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
精心选择的数据结构可以带来更高的运行或者存储效率。
数据结构往往同高效的检索算法和索引技术有关。
数据结构指数据对象中数据元素之间的关系。
数据结构种类
数组
数组是可以在内存中连续存储多个元素的结构,在内存中的分配也是连续的,数组中的元素通过数组下标进行访问,数组下标从0开始。
优点
1、按照索引查询元素速度快。
2、按照索引遍历数组方便。
缺点
1、数组的大小固定后就无法扩容了。
2、数组只能存储一种类型的数据。
3、添加,删除的操作慢,因为要移动其他的元素。
使用场景
频繁查询,对存储空间要求不大,很少增加和删除的情况。
栈
栈是一种特殊的线性比啊,仅能在线姓表的一端操作,栈顶允许操作,栈底不允许操作。
特点:先进后出,后进先出,从栈顶放入元素的操作叫入栈,取出元素叫出栈
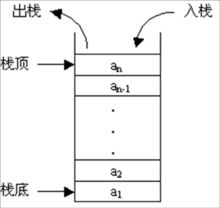
场景:栈常应用于实现递归功能方面的场景,例如斐波那契数列。
python栈实现
class Stack: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def push(self,item): self.items.append(item) def pop(self): self.items.pop() def peek(self): return self.items.pop() def size(self): return len(self.items)
队列
队列与栈一样,也是一种线性表,不同的是,队列可以在一端添加元素,在另一端取出元素。
特点:先进先出。从一端放入元素操作称为入队,取出元素为出队。
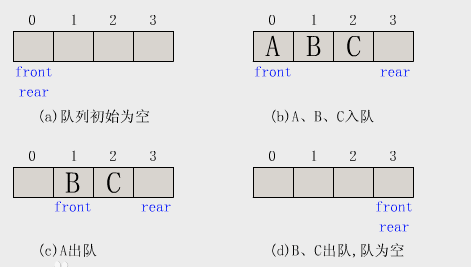
python队列实现
class Queue(): def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def enqueue(self,item): self.items.insert(0,item) def dequeue(self,item): self.items.pop() def size(self): return len(self.items)
双端队列
class Deque: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def addFront(self,item): self.items.append(item) def addRear(self,item): self.items.insert(0,item) def removeFront(self): return self.items.pop() def removeRear(self): return self.items.pop(0) def size(self): return len(self.items)
链表
链表是物理存储单元上非连续的,非顺序的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,每个元素包含两个结点,一个是存储元素的数据域(内存空间),另一个是指向下一个结点地址的指针域。根据指针的指向,链表能形成不同的结构,例如单链表、双向链表、循环链表。
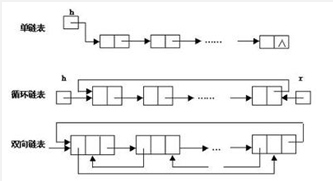
链表的优点
链表是很常用的一种数据结构,不需要初始化容量,可以任意加减元素。
添加或者删除元素时只需要改变前后两个元素节点的指针域指向地址即可,所以添加删除很快。
缺点
因为含有大量的指针域,占用空间较大。
查早元素需要遍历链表来查找,非常耗时。
场景
数据量小,需要频繁增加,删除操作。
树
树是一种数据结构,它是由n(n >= 1)个有限节点组成一个具有层次关系的集合。
特点:
-> 每个节点由零个或多个子节点
-> 没有父节点的节点称为根节点
-> 每一个非根节点有且只有一个父节点
-> 除了根节点外,每个子节点可以分为多个不相交的子数
日常应用中,用的更多的是树的另外一种结构,就是二叉树
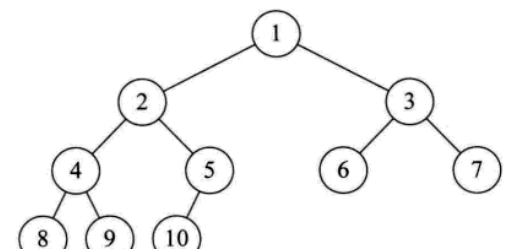
1、每个节点最多有两颗子数,节点的度最大为2。
2、左子数和右子数是有顺序的,次序不能颠倒。
3、即使某节点只有一个子数,也要区分左右子数。
二叉树是一种比较有用的折中方案,它添加,删除元素都很快,并且在查找方面也有很多的算法优化,所以,二叉树既有链表的好处,也有数组的好处,是两者的优化方案,在处理大批量的动态数据方面非常有用。
散列表
散列表,也叫哈希表,是根据关键码和值 (key和value) 直接进行访问的数据结构,通过key和value来映射到集合中的一个位置,这样就可以很快找到集合中的对应元素。
记录的存储位置=f(key)
这里的对应关系 f 成为散列函数,又称为哈希 (hash函数),而散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里,这种存储空间可以充分利用数组的查找优势来查找元素,所以查找的速度很快。
哈希表在应用中也是比较常见的,就如Java中有些集合类就是借鉴了哈希原理构造的,例如HashMap,HashTable等,利用hash表的优势,对于集合的查找元素时非常方便的,然而,因为哈希表是基于数组衍生的数据结构,在添加删除元素方面是比较慢的,所以很多时候需要用到一种数组链表来做,也就是拉链法。拉链法是数组结合链表的一种结构,较早前的hashMap底层的存储就是采用这种结构,直到jdk1.8之后才换成了数组加红黑树的结构,其示例图如下:

堆
堆是一种比较特殊的数据结构,可以被看做一棵树的数组对象,具有以下的性质:
-> 堆中某个节点的值总是不大于或不小于其父节点的值
-> 堆总是一棵完全二叉树
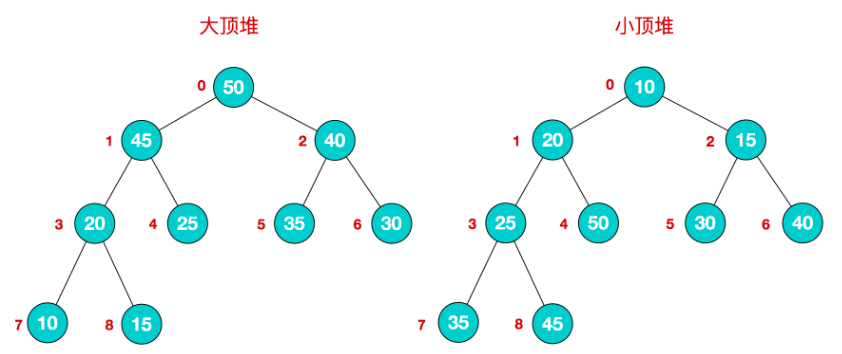
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4…n/2),满足前者的表达式的成为小顶堆,满足后者表达式的为大顶堆,这两者的结构图可以用完全二叉树排列出来,示例图如下:
图
图是由结点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将结点称为顶点,边是顶点的有序偶对,若两个顶点之间存在一条边,就表示这两个顶点具有相邻关系。
按照顶点指向的方向可分为无向图和有向图:

图是一种比较复杂的数据结构,在存储数据上有着比较复杂和高效的算法,分别有邻接矩阵 、邻接表、十字链表、邻接多重表、边集数组等存储结构
数据结构测试题
1、设计一种算法实现单链表反转
# 链表定义 class ListNode: def __init__(self,x): self.val=x self.next=None
方法一:对于一个长度为n的单链表head,用一个大小为n的数组arr存储从单链表从头到尾遍历所有的元素,再从arr尾到头读取元素组成一个新的单链表
时间消耗0(n)空间消耗0(n)
def reverse_linkedlist1(head): if head == None or head.next == None: #边界条件 return head arr = [] # 空间消耗为n,n为单链表的长度 while head: arr.append(head.val) head = head.next newhead = ListNode(0) tmp = newhead for i in arr[::-1]: tmp.next = ListNode(i) tmp = tmp.next return newhead.next
方法二:开始以单链表的第二个元素为循环变量,用2个变量循环向右操作,并设置一个辅助变量tmp,保存数据
时间消耗0(n)空间消耗0(n)
def reverse_linkedlist2(head): if head == None or head.next == None: #边界条件 return head p1 = head #循环变量1 p2 = head.next #循环变量2 tmp = None #保存数据的临时变量 while p2: tmp = p2.next p2.next = p1 p1 = p2 p2 = tmp head.next = None return p1
算法
如果a+b+c = 1000 且a**2 + b**2 = c**2 ,求出a b c的组合
三重循环
import time start_time = time.time() # 注意是三重循环 for a in range(0, 1001): for b in range(0, 1001): for c in range(0, 1001): if a**2 + b**2 == c**2 and a+b+c == 1000: print("a, b, c: %d, %d, %d" % (a, b, c)) end_time = time.time() print("elapsed: %f" % (end_time - start_time)) print("complete!")
-> 算法是独立存在的一种解决问题的方法和思想
-> 对于算法而言,实现的语言不重要,重要的是思想
算法特性
-> 确定性
-> 有穷性
-> 输入项
-> 输出项
-> 可行性
两重循环实现
import time start_time = time.time() # 注意是两重循环 for a in range(0, 1001): for b in range(0, 1001-a): c = 1000 - a - b if a**2 + b**2 == c**2: print("a, b, c: %d, %d, %d" % (a, b, c)) end_time = time.time() print("elapsed: %f" % (end_time - start_time)) print("complete!")
算法效率
实现算法程序的执行时间可以反应出算法的效率,即算法的优势。
单纯依靠运行的时间来比较算符的优劣并不一定是客观准确的。
时间复杂度
假设存在函数g,使得算法A处理规模为n的问题示例所有时间为T(n)= 0(g(n)),则称 0(g(n))为算法A的渐近时间复杂度,简称时间复杂度,记为T(n)
复杂度计算
-> 基本操作,即只有常数项,任务就是0(1)
-> 顺序结构,时间复杂度按加法计算
-> 循环结构,时间复杂度按乘法计算
-> 分支结构,时间复杂度取最大值
常见的时间复杂度算法

python实现算法
1、插入排序
插入排序的基本操作就是将一个数据插入到已经排序好的有序数据中,从而得到一个新的,个数加一的有序数据,算法适用于少量数据的排序,首先将第一个作为已经排序好的,然后每次从后的取出插入到前面的排序中
python实现
def insert_sort(ilist): for i in range(len(ilist)): for j in range(i): if ilist[i] < ilist[j]: ilist.insert(j, ilist.pop(i)) break return ilist ilist = insert_sort([4, 5, 6, 7, -3, 2, 6, 9, 8]) print(ilist)
2、冒泡排序
重复的访问要排序的数列,一次比较两个元素,顺序错误则交换,重复进行直到没有需要交换的
python实现
def bubble_sort(blist): count = len(blist) for i in range(0, count): for j in range(i + 1, count): if blist[i] > blist[j]: blist[i], blist[j] = blist[j], blist[i] return blist blist = bubble_sort([4, 5, 6, 7, 3, 2, 6, 9, 8]) print(blist)
3、快速排序
通过一次排序将数据分割成两部分,其中一部分的数据都比另一部分的数据小,然后按此方法重复,可以递归进行,达到整个数据变成有序序列。
python实现
def quick_sort(qlist): if qlist == []: return [] else: qfirst = qlist[0] qless = quick_sort([l for l in qlist[1:] if l < qfirst]) qmore = quick_sort([m for m in qlist[1:] if m >= qfirst]) return qless + [qfirst] + qmore qlist = quick_sort([3,2,8,5,-6,8]) print(qlist)

