平面图最小链覆盖 POI2002 Skiers
这道题感觉挺厉害的,记录一下。
题目大意
给一个图,它是个DAG(有向无环图),它是个平面图,它有一个起点和一个终点。求最小的从起点到终点的路径数量,使得存在一组这么多路径可以覆盖这个图的每一条边。
做法 1:
首先,最小链覆盖让我们想到:最小点覆盖。
于是我们多设置 \(m\) 个点表示 \(m\) 条边,就转化为 最小可重路径点覆盖,然后拆点 + 二分图匹配即可。
具体的,我们将每个点 \(U\) 拆成 \(U_x\) 和 \(U_y\) 两个点。若 \(A\) 和 \(B\) 有边,那么就连接 \(A_x\) 和 \(B_y\)。容易发现,这样建立新图最后是一个二分图,那么 最小不可重路径点覆盖其实就是 原图的顶点数量 - 二分图最大匹配数。
对于 最小可重路径点覆盖 而言,我们考虑如果 \(u\) 可以从原图走到 \(v\),那么就将 \(u\) 连向 \(v\)。可以发现,这样建图就可以转换为 最小不可重路径点覆盖 了。
这样的话可以完成 \(n \le 300\) 的题目。
做法 2:
发现上面的做法少用了一个性质:平面图。
偏序集中,我们考虑 Dilworth 定理:最长反链长度 等于 最小链覆盖个数。
根据下图感性理解一下,最长反链选择的“链”,在平面图里是一段相邻的平面,所以就考虑平面图的对偶图,对应上就是一段链!
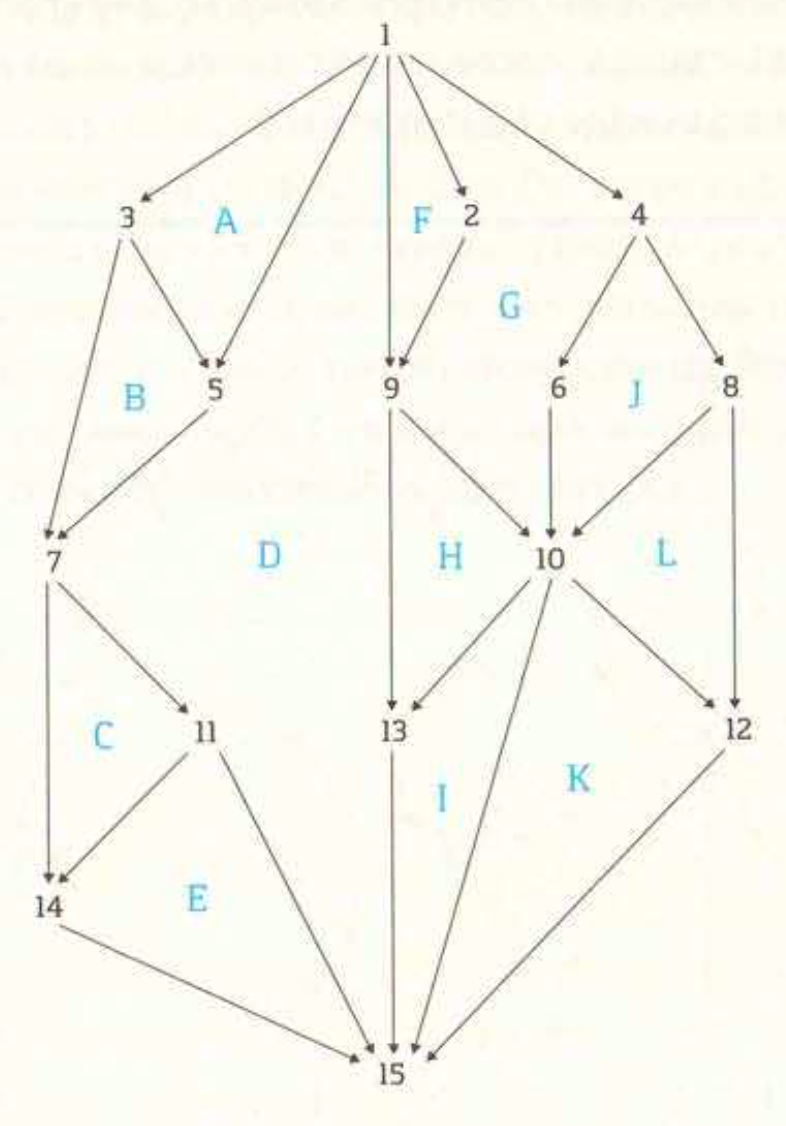
所以如果建出对偶图,那么结果就是,对偶图的最长链,就可以考虑 DAG 上 dp。
但是如果要求出平面图的每一个面再暴力拓扑的话就太麻烦了,其实我们考虑将平面从左往右进行 dp,然后将 dp 的值存到右侧的边上,然后如果存在环的话,可以发现,我们能分成“左侧” 和 “右侧”,然后用左侧的边更新右侧的边即可。
时间复杂度是 O(n),显然可以做到 \(n <= 10^5\) 的题目。
#include <bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, f = 1;
char ch = getchar();
while (!('0' <= ch && ch <= '9')) {
if (ch == '-') f = -1; ch = getchar();
}
while ('0' <= ch && ch <= '9') {
x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();
}
return x * f;
}
void wr(int x) {
if (x < 0) putchar('-'), x = -x;
if (x >= 10) wr(x / 10); putchar(x % 10 + '0');
}
const int N = 5e5 + 10;
struct node {
int id, to, nxt, from;
} edge[N << 1];
int cnt = 1, head[N];
int n, tot, f[N];
int vis[N], pre[N];
void add (int u, int v, int w) {
cnt++;
edge[cnt].id = w;
edge[cnt].to = v;
edge[cnt].from = u;
edge[cnt].nxt = head[u];
head[u] = cnt;
}
void dfs (int u, int fa) {
vis[u] = 1;
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to, w = edge[i].id; f[w] = 1;
if (!vis[v]) pre[v] = i, dfs (v, u);
else {
int x = v, mx = 0;
while (vis[x] == 2) mx = max(mx, f[edge[pre[x]].id]), x = edge[pre[x]].from;
int up = x; x = v; pre[v] = i;
while (x != up) f[edge[pre[x]].id] = mx + 1, x = edge[pre[x]].from;
}
}
vis[u] = 2;
}
int main() {
ios::sync_with_stdio(false); cin.tie(0);
cin >> n;
for (int i = 1; i < n; ++i) {
int num; cin >> num;
for (int j = 1; j <= num; ++j) {
int x; cin >> x; add (i, x, ++tot);
}
} dfs(1, 0); int ans = 0;
for (int i = 1; i <= tot; ++i) ans = max(ans,f[i]);
cout << ans << endl;
return 0;
}
总结
-
首先是 Dilworth 定理,可以将平面图的最长链覆盖 转换为 其对偶图的最长链。
-
在平面图的对偶图上操作的时候,可以考虑从左往右的顺序,然后把一些信息存到边上,就实现起来容易一点。

