部分聚类算法简介及优缺点分析

    之前项目有聚类的一些需求，现大致对一些聚类算法总结下：

    聚类是对一系列事物根据其潜在特征按照某种度量函数归纳成一个个簇的动作，使得簇内数据间的相似度尽可能大，不同簇的数据相似度尽可能小。

    通常聚类流程如下：数据获取-数据预处理-模型选型-模型聚类调参-输出结果。其中数据预处理、模型选型是流程中较为重要部分。数据预处理将杂乱无章的数据处理为具备某些共同点的特征，从而模型能更好地拟合数据，很经典的一句话：特征处理决定模型的上限。模型选型需要根据业务的具体需求及数据特性结合各聚类模型的特点进行选择。由于数据预处理需要根据具体数据及具体业务进行处理，本文仅介绍下各类聚类算法：

 

一、基于划分的聚类算法

K-means

经典K-means算法流程：
1. 随机地选择k个对象，每个对象初始地代表了一个簇的中心；
2. 对剩余的每个对象，根据其与各簇中心的距离，将它赋给最近的簇；
3. 重新计算每个簇的平均值，更新为新的簇中心；
4. 不断重复2、3，直到准则函数收敛

 

优点：

K-means算法简单快速；

当簇较为密集，呈现球状或团状时能有比较好的效果

缺点：

对K值敏感，聚类结果会受到K值很大的影响

对噪声点敏感，如当数据中只有2个簇，此时添加一个噪声点，则极大可能会导致噪声点分为一个簇，数据中的2个簇分为一个簇

只能聚凸的数据集

 

二、基于层次的聚类算法

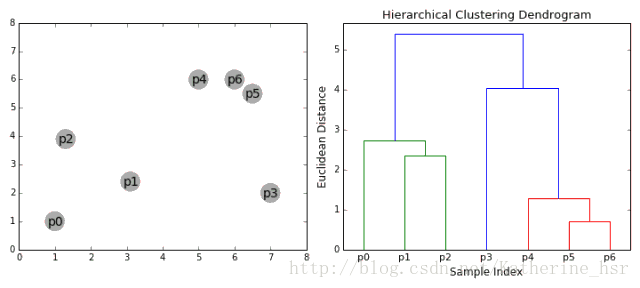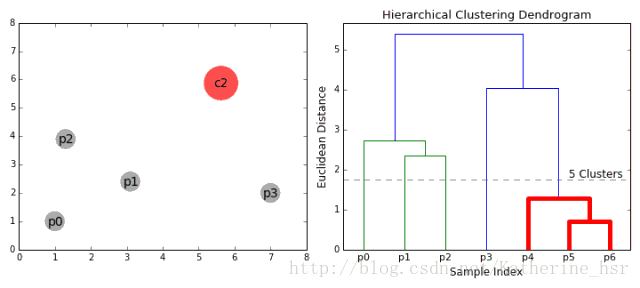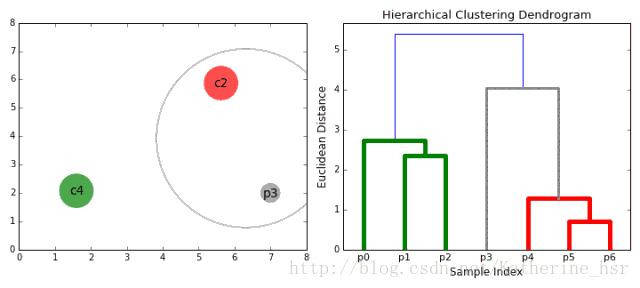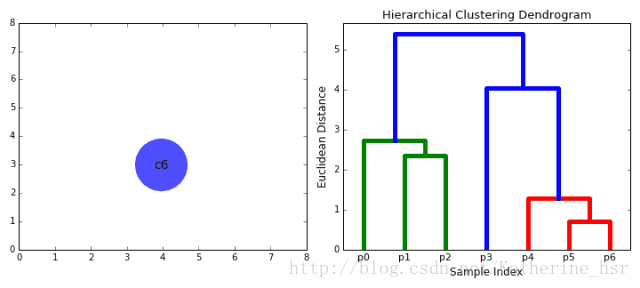
该类主要有自下而上和自上而下两种思想。

以自下而上流程为例：

1. 将每个对象看作一类，计算两两之间的最小距离；

2. 将距离最小的两个类合并成一个新类；

3. 重新计算新类与所有类之间的距离；

4. 重复2、3，直到所有类最后合并成一类

 

优点：

不需提前设置K值

可以发现层次关系

缺点：

计算复杂度高

奇异值有较大影响

 

三、基于密度的聚类算法

例如DBSCAN

DBSCAN 算法是一种基于密度的聚类算法：

　　1.聚类的时候不需要预先指定簇的个数

　　2.最终的簇的个数不确定

DBSCAN算法将数据点分为三类：

　　1.核心点：在半径Eps内含有超过MinPts数目的点。

　　2.边界点：在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内的点。

　　3.噪音点：既不是核心点也不是边界点的点。

DBSCAN流程：

1.将所有点标记为核心点、边界点或噪声点；

2.删除噪声点；

3.为距离在Eps之内的所有核心点之间赋予一条边；

4.每组连通的核心点形成一个簇；

5.将每个边界点指派到一个与之关联的核心点的簇中（哪一个核心点的半径范围之内）。

 

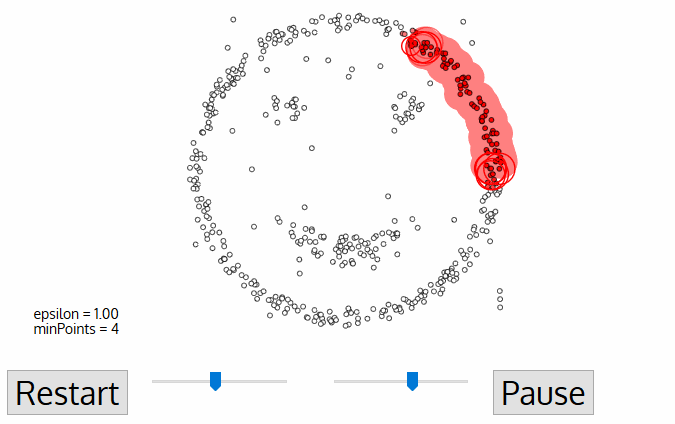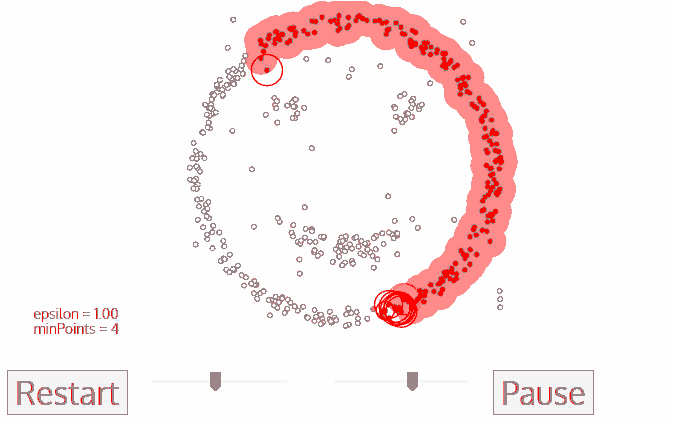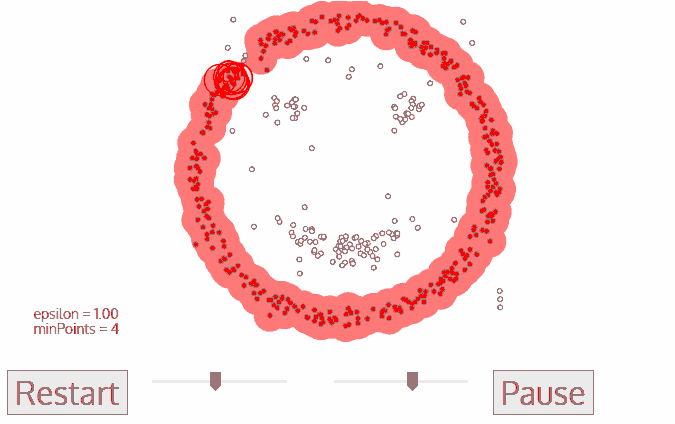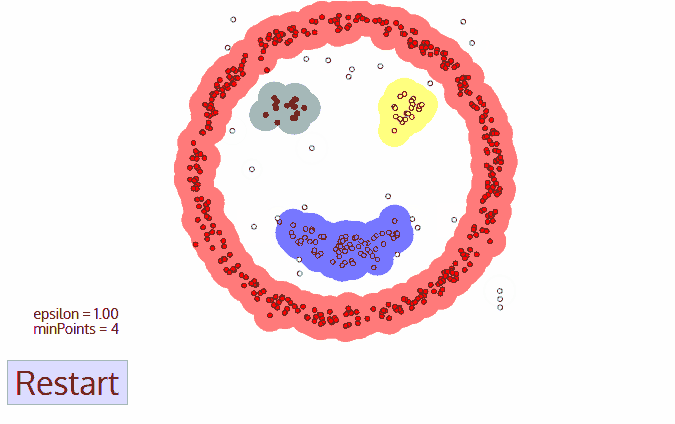
优点：

自适应的聚类，不需提前设置K值

对噪声不敏感

能发现任意形状的簇

缺点：

对两个参数圈的半径、阈值敏感

数据集越大，花费时间越长

 

四、基于滑动窗口的聚类算法

例如均值聚类漂移

均值聚类漂移算法流程：

     1.我们从一个以 C 点（随机选择）为中心，以半径 r 为核心的圆形滑动窗口开始。均值漂移是一种爬山算法，它包括在每一步中迭代地向更高密度区域移动，直到收敛。

     2.在每次迭代中，滑动窗口通过将中心点移向窗口内点的均值来移向更高密度区域。滑动窗口内的密度与其内部点的数量成正比。自然地，通过向窗口内点的均值移动，它会逐渐移向点密度更高的区域。

     3.我们继续按照均值移动滑动窗口直到没有方向在核内可以容纳更多的点。

     4.步骤 1 到 3 的过程是通过许多滑动窗口完成的，直到所有的点位于一个窗口内。当多个滑动窗口重叠时，保留包含最多点的窗口。然后根据数据点所在的滑动窗口进行聚类

 

 

 

优点：

不需提前设置K值

可以处理任意形状的簇类

 

缺点：

窗口半径有可能是不重要的

对于较大的特征空间，计算量较大