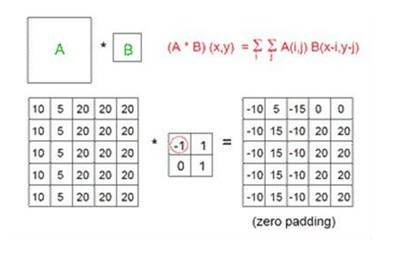
卷积网络(convolutional network),也叫卷积神经网络(convolutional neural network,CNN),是一种专门用来处理具有类似网格结构的数据的神经网络。
卷积网络是指那些至少使用在网路的一层中使用卷积运算来代替一般的矩阵算法运算的神经网络。
1.卷积运算
摘自百度百科。
设:f(x),g(x)是R1上的两个可积函数,作积分:
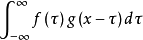
可以证明,关于几乎所有的实数x,上述积分是存在的。这样,随着x的不同取值,这个积分就定义了一个新函数h(x),称为函数f与g的卷积,记为h(x)=(f*g)(x)。
容易验证,(f * g)(x) = (g * f)(x),并且(f * g)(x)仍为可积函数。这就是说,把卷积代替乘法
卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n),则卷积的结果:
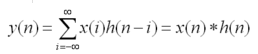
针对离散值卷积问题:(摘自CNBLOG),可以看做一个矩阵乘法:
2.动机
卷积运算通过三个重要的思想来帮助改进机器学习系统:稀疏表示(sparse interactions),参数共享(parameter sharing
3.池化(pooling)
池化函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。
常用的池化函数:最大池化,相邻函数使用,当输入做出少量平移时,池化能够帮助输入的表示近似不变(invariant)。平移的不变性是指当我们对输入进行少量的平移时,经过池化函数后的大多数输出并不会发生改变。
使用池化可以说增加了一个无限强的先验,这一层学得的函数必须具有对少量平移的不变性。
最大池化单元只对周围的最大值比较敏感,而不是精确的位置。
池化综合了全部邻居的反馈信息,使得池化单元少于探测单元成为可能,可以通过综合池化区域的K个像素的统计特征而不是单个像素来实现。提高网络计算效率,因为下层少了K倍的输入。