社会科学问题研究的计算实践——8、流行性(计算实践:富者愈富过程的模拟)
学习资源来自,一个哲学学生的计算机作业 (karenlyu21.github.io)
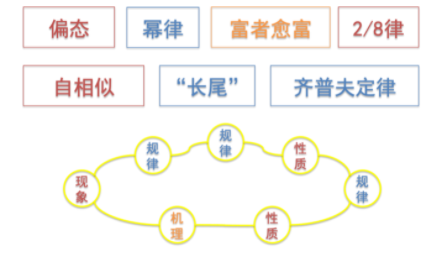
1、背景问题
不同事物的流行程度存在差别。流行性往往呈现为幂律分布:受关注少的事物远多于受关注多的事物,有同样关注量的事物的数量总和在全体中的占比(y),是其关注量(x)的幂函数,亦即
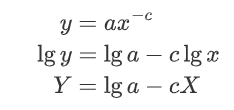
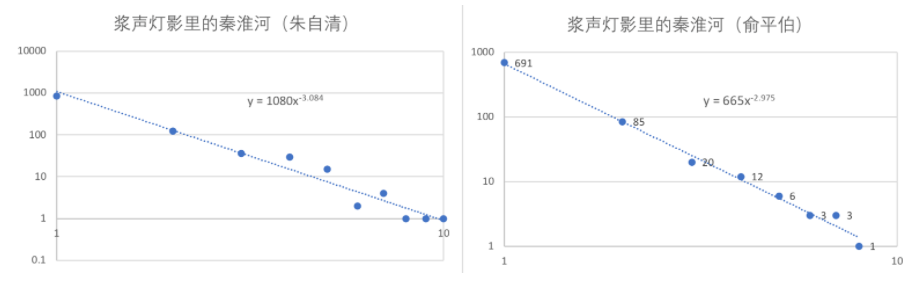
一个例子是文本中的词语出现次数
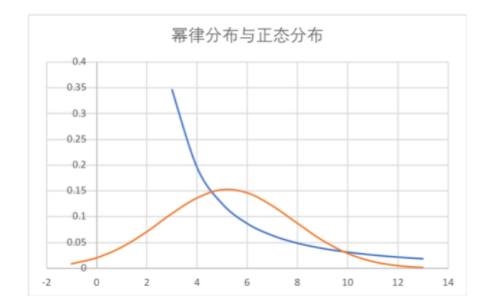
与正态分布相比,幂律分布是“偏态”的(不平等)。它有如下几个特点:
- 较小取值者有很大的占比;
- “中等收入群体”不够大;
- 较大取值者的占比也不是极低,“总有几个富人”。亦即“长尾”(long tail)性质,limx→∞(x+y)/x=1。
此外,幂律还是无标度(scale-free)、自相似的(self-similar),F(ax)=bF(x)。
关注程度-数量的幂律分布,经过几步数学变换,就可以变成排位序-关注程度的分布。
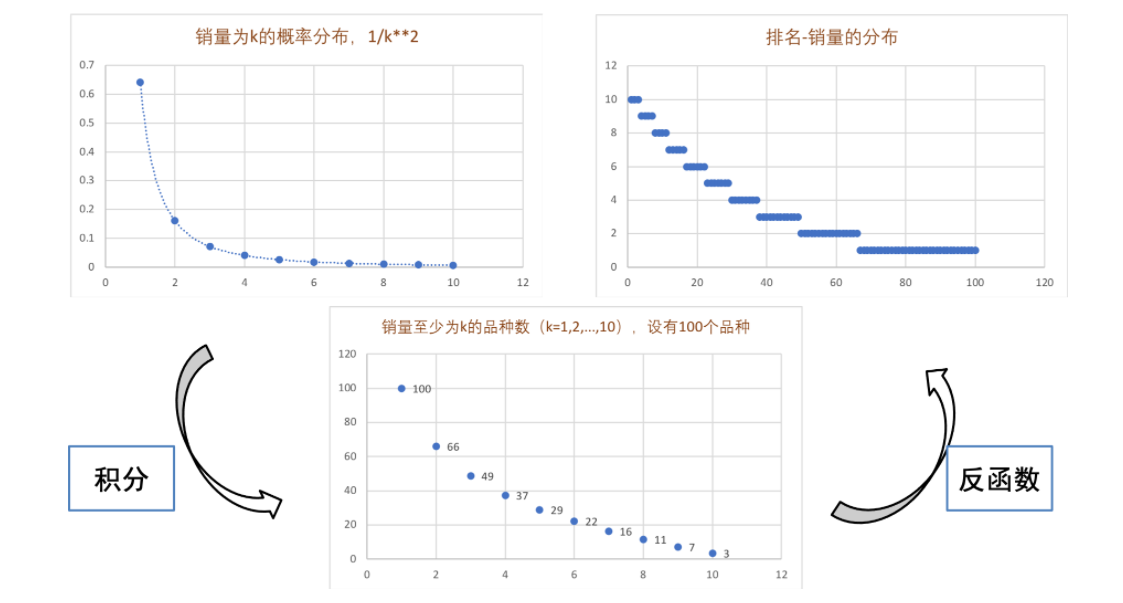
排位序-关注程度的分布也呈幂律分布。位次越高的事物,越受欢迎。这一定律由齐普夫首先发现,故被称为齐普夫律(Zipf's law)。他发现,在《尤利西斯》中,把词语按照出现频次f由高到低排序,每一词语的位次为r(r=1为出现次数最多的词语),有如下规律存在:f(r)=A/r
其中A为常数。后来的补充性研究做了进一步的厘正:f(r)=Ar-b,b≈1
位序-关注程度的分布让我们发现,生活中某些常常谈及的东西,和学术研究的某些经典成果,也来自幂律分布的性质,例如
- 2/8律:前20%的人/事物占有80%的关注。
- “长尾下的小生意”:排位序-关注程度的分布也有长尾性质,这意味着,排位不高的事物,受关注度的总和依然可以很大。亦即,对于∀k,只要max足够大,∫kmax a/x dx依然可以很大。Amazon、淘宝做的就是“长尾下的小生意”。
以上,我们讨论了流行性问题的现象、性质和规律。而流行性问题的成因或机理是什么呢?一个重要的理论是“富者愈富”:正因为人们喜欢追捧本来就很受欢迎的事物,事物的受欢迎程度才呈幂律分布。
在作业中,我们就要来模拟“富者愈富”的过程,看看最终是否会得到幂律分布的结果。
2、计算实践:富者愈富过程的模拟
2.1、作业描述与算法思路
按照顺序创建一系列网页:1,2,3,…,j,…,n=10000
当创建网页j时,以概率p或1−p选择a或b执行:
- a. 以概率p,均匀地、随机地选择一个早先创建的网页i,建立一个从j到i的链接
- b. 以1−p的概率,按照与已有入度成正比的概率,选择一个早先创建的网页i,建立一个从j到i的链接。
分别取p=0.25,0.75运行程序。分析结果,观察最后的结果是否符合幂律分布。
| 节点入度 | 0 | 1 | 2 | 3 | 4 | … | m |
|---|---|---|---|---|---|---|---|
| 节点个数 | n0 | n1 | n2 | n3 | n4 | … | nm |
本次作业有一个特别要求:尽量不用太大的存储空间。如果我们在每一步创建下一个网页时,都要记住前面所有网页分别链接到了哪个网页,运行到后面总网页数较大时,就会占用很大的存储空间,运行速度会比较慢。
事实上,我们只用在每一步记住不同频数的网页有多少个,列表的长度最多为m,这远小于n。因为我们不用明确地知道当前创建的网页j链接到了之前的哪个网页i上,而只需要知道j链接到了入度为何(设为f)的网页上,然后对入度-个数的表格进行操作(nf减小1,nf+1增加1),具体可见我代码中的degreeDictModifier函数。
此外,只存储节点入度-节点个数的信息时,如何实现随机选择一个网页,如何与入度成正比选择一个网页?我用到了random库的choices方法,采用了不同的加权值,实现了两种选择方式。具体可见我代码中的webCreate函数。
2.2、编程实现与要点说明
首先,定义一个函数degreeDictModifier,用以更新节点入度-节点个数的信息(被存储在“入度字典”degreeDict里):输入原先的入度字典degreeDict和被选中网页的入度choice,返回更新后的入度字典degreeDict。
# 被选中的网页增加一个入度,对degreeDict的影响如下
def degreeDictModifier(degreeDict, choice):
入度为choice的网页数减小1:
degreeDict[choice] -= 1
入度为choice + 1的网页数增加1:
designated = choice + 1
if designated in degreeDict.keys():
degreeDict[designated] += 1
else:
degreeDict[designated] = 1
return degreeDict
接着,定义函数webCreate,创建新网页,并将其链接到之前创建的一个网页,调用degreeDictModifier函数,对degreeDict做出更新。
def webCreate(degreeDict, p):
degreeKinds = list(degreeDict.keys()) # 现有网页有的度数一共有这么些种
degreeCount = list(degreeDict.values()) # 每一元素表示,度数为某一种的网页一共有几个
调用random库生成一个[0,1]的随机数,它小于p的概率为p,大于p的概率为1−p。
- 以概率p随机选择一个网页链接。我调用了
random库的choices方法。对于每一种节点入度,按照这一入度共有多少网页进行加权weights=degreeCount,这样,选择某一入度的网页的概率与这一入度的总网页数成正比,而选择某一个网页的概率是相等的。
randNum = random.random()
if randNum < p:
randChoiceList = random.choices(degreeKinds, weights=degreeCount, k=1)
# 给度数加权后,选择某一网页的概率是相等的
randChoice = randChoiceList[0]
degreeDict = degreeDictModifier(degreeDict, randChoice)
- 以概率1−p与入度成正比选择一个网页。对于某一入度
kind,计算这一入度的网页数cnt和该入度的乘积(cnt * kind),存储在newWeights里,用这一数据给每一入度的网页加权。这样加权后,某一个网页被选中的概率与其入度成正比。
else:
newWeights = []
for kind, cnt in degreeDict.items():
newWeights.append(cnt * kind)
slantedChoiceList = random.choices(degreeKinds, weights=newWeights, k=1)
# 采用这一新的加权法后,某一网页被选中的概率与度数成正比
slantedChoice = slantedChoiceList[0]
degreeDict = degreeDictModifier(degreeDict, slantedChoice)
degreeDict[0] += 1
return degreeDict
定义函数webCreateSeries,循环调用webCreate,完成10000个网页的创建,并把最终的degreeDict输出到结果文件output.csv中,返回作图需要的数据。
def webCreateSeries(n, p, outputF):
print('* * * * * * A new round begins. n = %i, p = %.2f * * * * * *' % (n, p))
cnt = 0
outputF.write('n = %i p = %.2f\n' % (n, p))
循环完成10000个网页的创建,得到最终的degreeDict:
# 循环完成10000个网页的创建
degreeDict = {0: 1}
while True:
cnt += 1
if cnt >= n:
break
if cnt % 100 == 0:
print('%i pages have been created.' % cnt, end='\r')
degreeDict = webCreate(degreeDict, p)
print()
输出最终的degreeDict到distribution.csv:
# 输出结果到csv
degreeList = list(degreeDict.items())
degreeList.sort(key=lambda x: x[0])
## 删除网页数为0的度数,不然csv里一行太长了不好看
for i in range(degreeList[0][0], degreeList[-1][0] + 1):
if degreeDict[i] == 0:
del degreeDict[i]
degreeKinds = degreeDict.keys() # 现有网页有的度数一共有这么些种
degreeCount = degreeDict.values() # 每一元素表示,度数为某一种的网页一共有几个
outputF.write('degree,')
for degreeKind in degreeKinds:
outputF.write('%i,' % degreeKind)
outputF.write('\namount,')
for degreeCNT in degreeCount:
outputF.write('%i,' % degreeCNT)
outputF.write('\n')
整理数据,以方便主程序中作图,返回作图需要的数据xPoints, yPoints。
# 为了画图,补上网页数为0的度数
degreeList = list(degreeDict.items())
degreeList.sort(key=lambda x: x[0])
for i in range(degreeList[0][0], degreeList[-1][0] + 1):
if i not in degreeDict.keys():
degreeDict[i] = 0 # for log scale
elif degreeDict[i] == 0:
degreeDict[i] == 0 # for log scale
degreeList = list(degreeDict.items())
degreeList.sort(key=lambda x: x[0])
degreeKinds = [degreeList[i][0] for i in range(len(degreeList))]
degreeCount = [degreeList[i][1] for i in range(len(degreeList))]
# 横轴纵轴数据
xPoints = np.array(degreeKinds)
yPoints = np.array(degreeCount)
print('This round all done.')
return xPoints, yPoints
主程序就比较简单了,直接给定n、p值调用webCreateSeries即可,得到相应的横轴纵轴数据x1, y1和x2, y2。
outputF = open('./distribution.csv', 'w')
fig = plt.figure()
ax1 = plt.subplot(2, 2, 1)
ax3 = plt.subplot(2, 2, 2)
ax5 = plt.subplot(2, 2, 3)
# fig, ((ax1, ax3), (ax5,)) = plt.subplots(2,2)
# n = 10000, p = 0.25
x1, y1 = webCreateSeries(10000, 0.25, outputF)
# n = 10000, p = 0.75
x2, y2 = webCreateSeries(10000, 0.75, outputF)
outputF.close()
接下来就是作图。先作入度-个数图(ax1和ax2)。该图应当符合幂律分布。
# original scale
print('Drawing the picture...')
color1 = 'tab:red'
ax1.set_title('original scale')
ax1.plot(x1, y1, color=color1)
ax1.set_xlabel('degree')
ax1.set_ylabel('amount of web pages (p = 0.25)', color=color1)
ax1.tick_params(axis='y')
ax2 = ax1.twinx() # 把两次的结果画进同一个坐标系
color2 = 'tab:blue'
ax2.plot(x2, y2, color=color2)
ax2.set_ylabel('amount of web pages (p = 0.75)', color=color2)
ax2.tick_params(axis='y')
对入度和幂律取双对数作图(ax3和ax4)。该图应当是一条直线。
# log scale
ax3.set_title('log scale')
ax3.plot(x1, y1, color=color1)
ax3.set_xlabel('degree')
ax3.set_ylabel('amount of web pages (p = 0.25)', color=color1)
ax3.tick_params(axis='y')
ax3.set_xscale('log')
ax3.set_yscale('log')
ax4 = ax3.twinx()
ax4.plot(x2, y2, color=color2)
ax4.set_ylabel('amount of web pages (p = 0.75)', color=color2)
ax4.tick_params(axis='y')
ax4.set_xscale('log')
ax4.set_yscale('log')
print('finished drawing the log scale')
取双对数作图后,入度较大时,图形呈锯齿状,有的入度恰好存在网页,有的入度不存在网页。为了让图更好看,让网页数amount(degree)对degree在[degreei,degreemax]积分,w=∫degreei degreemax amount (degree),它指的是有多少网页的入度大于degreei。
得到入度-大于该入度的总网页数w后,取双对数作图ax5和ax6。分析w的表达式,这一图形应为一条直线。
# 为了图更好看(不呈锯齿状),让网页数y对(最大度数 – x)积分。积分后,每一度数x对应的新y值 = 有多少网页的入度大于这一度数
ax5.set_title('integral (log scale)')
y1_new = np.copy(y1)
for i in range(len(x1)):
pageSum1 = np.sum(y1[i:])
y1_new[i] = pageSum1
y2_new = np.copy(y2)
for i in range(len(x2)):
pageSum2 = np.sum(y1[i:])
y2_new[i] = pageSum2
ax5.plot(x1, y1_new, color=color1)
ax5.set_xlabel('degree')
ax5.set_ylabel('sum of web pages (p = 0.25)', color=color1)
ax5.tick_params(axis='y')
ax5.set_xscale('log')
ax5.set_yscale('log')
ax6 = ax5.twinx()
ax6.plot(x2, y2_new, color=color2)
ax6.set_ylabel('sum of web pages (p = 0.75)', color=color2)
ax6.tick_params(axis='y')
ax6.set_xscale('log')
ax6.set_yscale('log')
print('finished drawing the log scale for the sum of web pages')
fig.tight_layout()
# fig.set_size_inches(7, 8)
plt.show()
fig.savefig('./distribution.png', dpi=300)
2.3、结果与分析
distribution.csv中结果如下:
n = 10000 p = 0.25
degree,0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,27,28,29,30,31,32,34,36,37,38,39,43,45,50,52,83,101,107,109,117,155,172,188,236,592,757,820,
amount,7984,973,392,202,114,52,54,48,21,16,23,13,9,9,7,7,5,4,8,4,4,4,3,4,1,3,1,1,3,2,3,2,2,1,1,1,1,1,2,1,1,1,1,1,2,1,1,1,1,1,1,1,1,
---------------------------------------------------------------------------------------
n = 10000 p = 0.75
degree,0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,24,25,27,30,35,40,
amount,5684,2169,954,488,268,155,78,62,42,18,19,13,7,8,6,2,3,2,5,3,3,4,1,1,1,1,1,1,1,
在我们的算法产生完10000个网页后,“入度 — 网页数”基本上呈幂律分布。这一点在左下图中体现得尤为明显。取双对数做图后,“入度 — 大于这一入度的网页总数”的图像基本是一条直线。
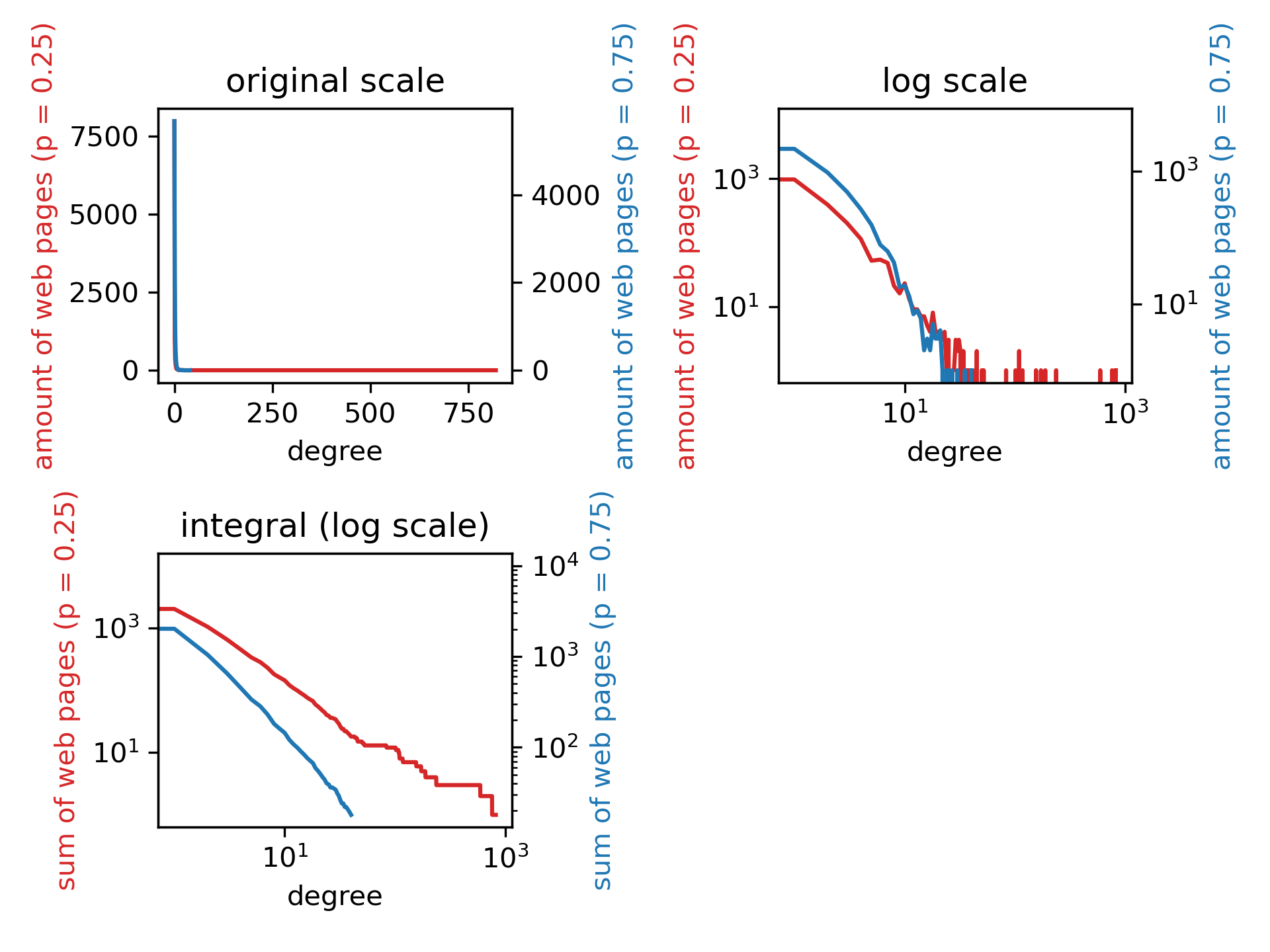
接下来分析p值对于这一分布的影响。通过比较n=10000,p=0.25与n=10000,p=0.75的输出结果,p的值对于最后的分布很可能有以下影响(是否真的有这些影响,还需要更严格的数学证明,或取更多组数据做统计学分析):
- p越小,最受欢迎的网页的入度(m)越大,较受欢迎的网页(例如入度≥10)的总数越大。这是因为,p越小,创建某一网页时选择“跟风”路径的概率更高,即以与入度成正比的概率链接到网页。网页已有入度越高,越容易被链接到,富者越富。最终状态里,富人也会更多。
- p越小,无人问津的网页越多,p=0.25时有8005个,p=0.75时有5714个。(这在图中没有表示出来,第一张图两条线叠在一起了,第二张图里入度为0的点没法取对数。)这是因为,p越小,创建某一网页时选择“平均主义”的概率越低,一开始就无人问津的网页更难被链接到,从而逐渐累积起来。
3、完整代码
富者愈富
import random
import matplotlib.pyplot as plt
import numpy as np
print('Initiating...')
# 被选中的网页增加一个入度,对degreeDict的影响如下
def degreeDictModifier(degreeDict, choice):
degreeDict[choice] -= 1
designated = choice + 1
if designated in degreeDict.keys():
degreeDict[designated] += 1
else:
degreeDict[designated] = 1
return degreeDict
def webCreate(degreeDict, p):
degreeKinds = list(degreeDict.keys()) # 现有网页有的度数一共有这么些种
degreeCount = list(degreeDict.values()) # 每一元素表示,度数为某一种的网页一共有几个
randNum = random.random()
if randNum < p:
randChoiceList = random.choices(degreeKinds, weights=degreeCount, k=1)
# 给度数加权后,选择某一网页的概率是相等的
randChoice = randChoiceList[0]
degreeDict = degreeDictModifier(degreeDict, randChoice)
else:
newWeights = []
for kind, cnt in degreeDict.items():
newWeights.append(cnt * kind)
slantedChoiceList = random.choices(degreeKinds, weights=newWeights, k=1)
# 采用这一新的加权法后,某一网页被选中的概率与度数成正比
slantedChoice = slantedChoiceList[0]
degreeDict = degreeDictModifier(degreeDict, slantedChoice)
degreeDict[0] += 1
return degreeDict
def webCreateSeries(n, p, outputF):
print('* * * * * * A new round begins. n = %i, p = %.2f * * * * * *' % (n, p))
cnt = 0
outputF.write('n = %i p = %.2f\n' % (n, p))
# 循环完成10000个网页的创建
degreeDict = {0: 1}
while True:
cnt += 1
if cnt >= n:
break
if cnt % 100 == 0:
print('%i pages have been created.' % cnt, end='\r')
degreeDict = webCreate(degreeDict, p)
print()
# 输出结果到csv
degreeList = list(degreeDict.items())
degreeList.sort(key=lambda x: x[0])
## 删除网页数为0的度数,不然csv里一行太长了不好看
for i in range(degreeList[0][0], degreeList[-1][0] + 1):
if degreeDict[i] == 0:
del degreeDict[i]
degreeKinds = degreeDict.keys() # 现有网页有的度数一共有这么些种
degreeCount = degreeDict.values() # 每一元素表示,度数为某一种的网页一共有几个
outputF.write('degree,')
for degreeKind in degreeKinds:
outputF.write('%i,' % degreeKind)
outputF.write('\namount,')
for degreeCNT in degreeCount:
outputF.write('%i,' % degreeCNT)
outputF.write('\n')
# 为了画图,补上网页数为0的度数
degreeList = list(degreeDict.items())
degreeList.sort(key=lambda x: x[0])
for i in range(degreeList[0][0], degreeList[-1][0] + 1):
if i not in degreeDict.keys():
degreeDict[i] = 0 # for log scale
elif degreeDict[i] == 0:
degreeDict[i] == 0 # for log scale
degreeList = list(degreeDict.items())
degreeList.sort(key=lambda x: x[0])
degreeKinds = [degreeList[i][0] for i in range(len(degreeList))]
degreeCount = [degreeList[i][1] for i in range(len(degreeList))]
# 横轴纵轴数据
xPoints = np.array(degreeKinds)
yPoints = np.array(degreeCount)
print('This round all done.')
return xPoints, yPoints
# 手动输入n/p值
# # p值
# try:
# p = input('请输入一个0~1之间的p值(创建网页时,以p的概率,随机链接网页,以1-p的概率,按照与度数成正比的概率链接网页):')
# p = float(p)
# except:
# print('输出错误,采用默认p值0.5。')
# p = 0.5
# # n值
# try:
# p = input('请输入一个正整数n值,这是我们一共要创建的网页数:')
# p = int(p)
# except:
# print('输出错误,采用默认n值10000。')
# p = 10000
outputF = open('./distribution.csv', 'w')
fig = plt.figure()
ax1 = plt.subplot(2, 2, 1)
ax3 = plt.subplot(2, 2, 2)
ax5 = plt.subplot(2, 2, 3)
# fig, ((ax1, ax3), (ax5,)) = plt.subplots(2,2)
# n = 10000, p = 0.25
x1, y1 = webCreateSeries(10000, 0.25, outputF)
# n = 10000, p = 0.75
x2, y2 = webCreateSeries(10000, 0.75, outputF)
outputF.close()
# 让x轴的元素数变成一样
# if len(x1) > len(x2):
# x = x1
# y_add = np.array([0 for i in range(len(x1) - len(x2))])
# y2 = np.concatenate((y2, y_add), ax1is=None)
# else:
# x = x2
# y_add = np.array([0 for i in range(len(x2) - len(x1))])
# y1 = np.concatenate((y1, y_add), ax1is=None)
# 画图
# original scale
print('Drawing the picture...')
color1 = 'tab:red'
ax1.set_title('original scale')
ax1.plot(x1, y1, color=color1)
ax1.set_xlabel('degree')
ax1.set_ylabel('amount of web pages (p = 0.25)', color=color1)
ax1.tick_params(axis='y')
ax2 = ax1.twinx() # 把两次的结果画进同一个坐标系
color2 = 'tab:blue'
ax2.plot(x2, y2, color=color2)
ax2.set_ylabel('amount of web pages (p = 0.75)', color=color2)
ax2.tick_params(axis='y')
print('finished drawing the original scale')
# log scale
ax3.set_title('log scale')
ax3.plot(x1, y1, color=color1)
ax3.set_xlabel('degree')
ax3.set_ylabel('amount of web pages (p = 0.25)', color=color1)
ax3.tick_params(axis='y')
ax3.set_xscale('log')
ax3.set_yscale('log')
ax4 = ax3.twinx()
ax4.plot(x2, y2, color=color2)
ax4.set_ylabel('amount of web pages (p = 0.75)', color=color2)
ax4.tick_params(axis='y')
ax4.set_xscale('log')
ax4.set_yscale('log')
print('finished drawing the log scale')
# 为了图更好看(不呈锯齿状),让网页数y对(最大度数 – x)积分。积分后,每一度数x对应的新y值 = 有多少网页的入度大于这一度数
ax5.set_title('integral (log scale)')
y1_new = np.copy(y1)
for i in range(len(x1)):
pageSum1 = np.sum(y1[i:])
y1_new[i] = pageSum1
y2_new = np.copy(y2)
for i in range(len(x2)):
pageSum2 = np.sum(y1[i:])
y2_new[i] = pageSum2
ax5.plot(x1, y1_new, color=color1)
ax5.set_xlabel('degree')
ax5.set_ylabel('sum of web pages (p = 0.25)', color=color1)
ax5.tick_params(axis='y')
ax5.set_xscale('log')
ax5.set_yscale('log')
ax6 = ax5.twinx()
ax6.plot(x2, y2_new, color=color2)
ax6.set_ylabel('sum of web pages (p = 0.75)', color=color2)
ax6.tick_params(axis='y')
ax6.set_xscale('log')
ax6.set_yscale('log')
print('finished drawing the log scale for the sum of web pages')
fig.tight_layout()
# fig.set_size_inches(7, 8)
plt.show()
fig.savefig('./distribution.png', dpi=300)

 计算实践:富者愈富过程的模拟
计算实践:富者愈富过程的模拟

