算法设计与分析——矩阵链相乘求解
题目描述:
给出矩阵链相乘的最优括号次序。矩阵链A1A2A3A4A5,其维数分别为2×3,3×6,6×4,4×2,2×7。(给出计算过程)
记住递推式:
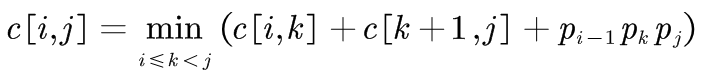
由题意可得:
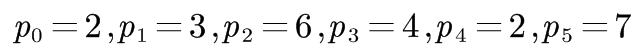
运用表格法(建议:自底向上横向填写):
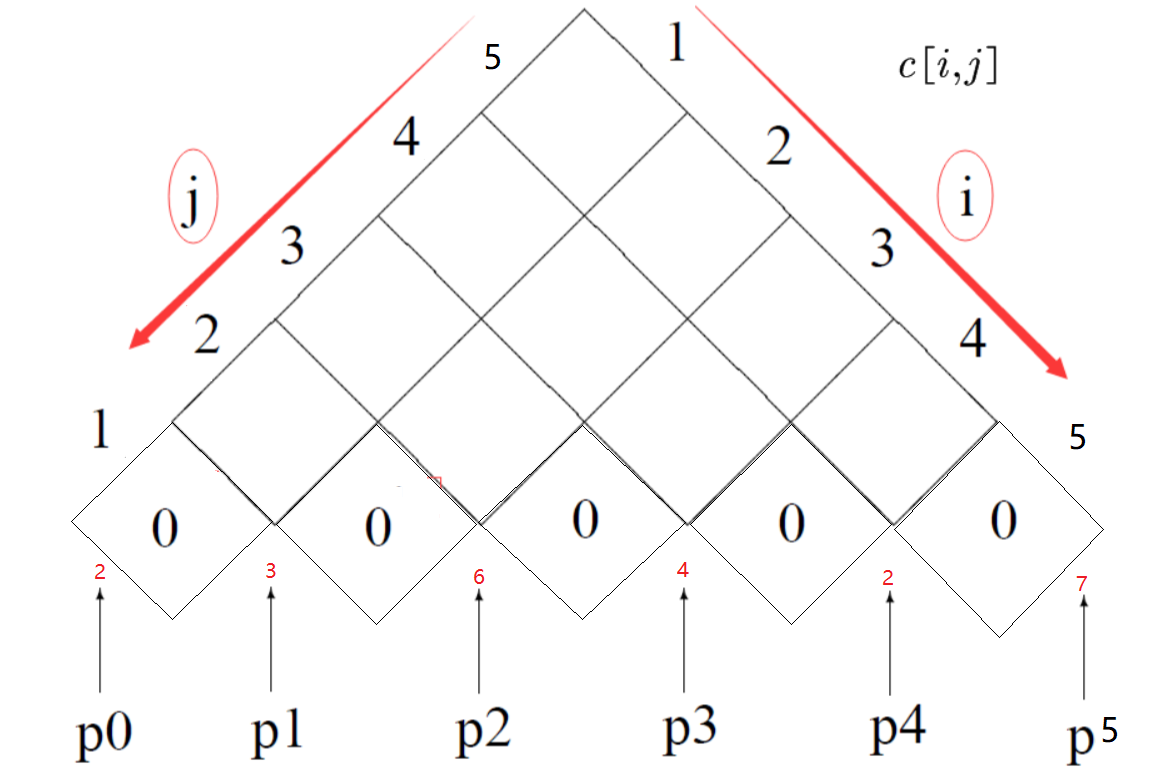
已知数据:
c[1,1]=0;c[2,2]=0;c[3,3]=0; c[4,4]=0; c[5,5]=0
开始计算:
①
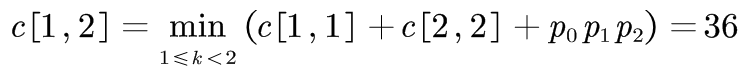
②
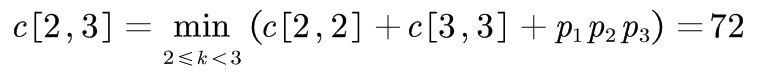
③
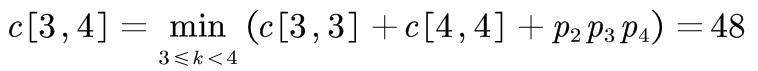
④
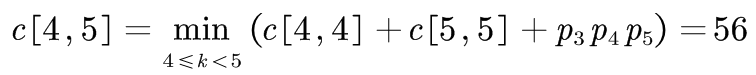
⑤
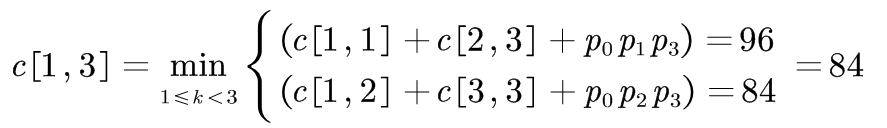
⑥
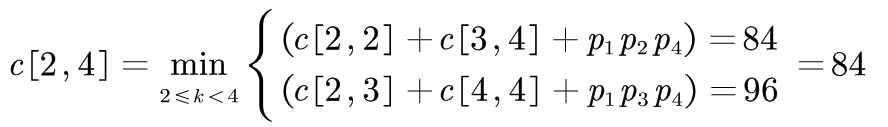
⑦

⑧
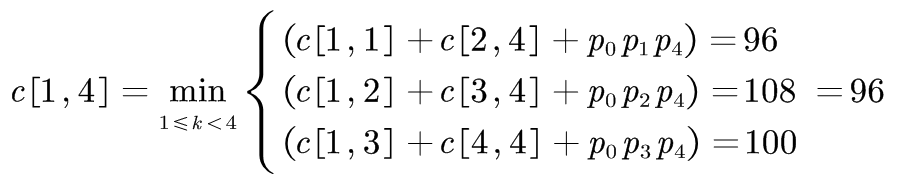
⑨
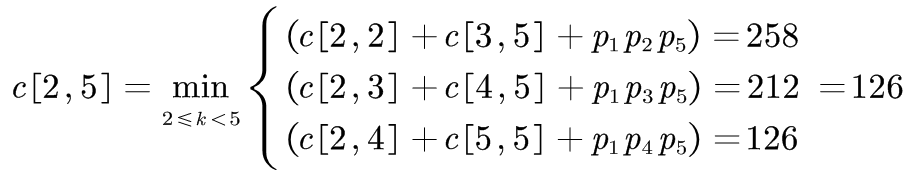
⑩
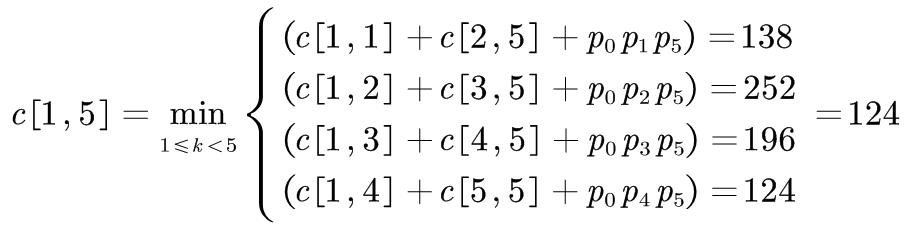
最终结果:
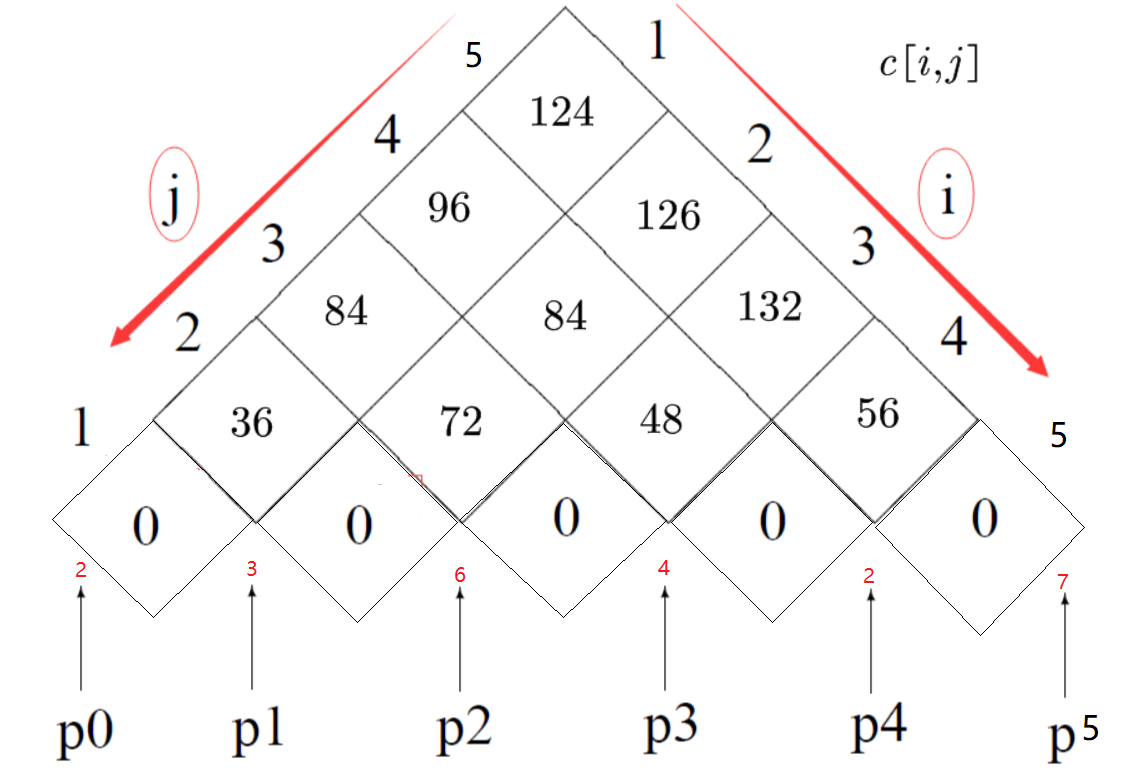
填写表格:
| c[1,1]=0 | c[1,2]=36 | c[1,3]=84 | c[1,4]=96 | c[1,5]=124 |
|---|---|---|---|---|
| c[2,2]=0 | c[2,3]=72 | c[2,4]=84 | c[2,5]=126 | |
| c[3,3]=0 | c[3,4]=48 | c[3,5]=132 | ||
| c[4,4]=0 | c[4,5]=56 | |||
| c[5,5]=0 |
(1)找出这5个矩阵相乘需要的最少数量乘法的次数。
答:c[1,5]=124
(2)给出一个括号表达式,使得这种次序下达到乘法的次数最少。
答:A1(A2(A3A4))A5
C语言实现:
#include <stdio.h>
#include <stdlib.h>
int m[6][6]={0};
int s[6][6]={0};
void Print_Optimal_Parens(int s[][6],int i,int j) //构造最优解
{
if ( i ==j)
{
printf("A%d",i);
}
else
{
printf("(");
Print_Optimal_Parens(s,i,s[i][j]);
Print_Optimal_Parens(s,s[i][j]+1,j);
printf(")");
}
}
void Matrix_Chain_Order(int p[],int n)
{
int i,j,L,k,q;
for (i=1;i<=n;i++) //先对单个矩阵的链,求解,即全部m[i][i] =0;
{
m[i][i]=0;
}
for(L=2;L<=n;L++) //从两个矩阵链開始,逐次添加矩阵链的长度
for(i=1;i<=n-L+1;i++) //在给定p[]中的矩阵链中,对全部种长度为L的情况计算
{
j = i+L-1;
m[i][j] = -1;
for(k=i;k<=j-1;k++) //遍历全部可能的划分点k。计算出最优的划分方案,
{
q = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if ( q < m[i][j] || m[i][j] == -1)
{
m[i][j] = q; //最优的代价q保存在m[i][j]中
s[i][j] = k; //最优的划分位置k保存在s[i][j]中
}
}
}
}
void main()
{
int p[]={2,3,6,4,2,7}; //矩阵的输入
int length = sizeof(p)/sizeof(p[0])-1; //矩阵长度
int i,j;
Matrix_Chain_Order(p,length);
for(i =1;i<=5;i++)
{
for (j=1;j<=5;j++)
{
printf("%8d",m[i][j]);
}
printf("\n");
}
Print_Optimal_Parens(s,1,5);
printf("\n");
}
检验结果正确!

 矩阵链相乘的简单求解
矩阵链相乘的简单求解

