算法设计与分析——简答概述
1、什么是算法分析?算法分析主要包括哪两个方面?
答:算法分析是对一个算法需要多少计算时间和存储空间作足量分析。算法分析主要包括:时间复杂度和空间复杂度。
2、什么是最小生成树?最小生成树的求解用到什么算法?
答:设G=(V,E)是一个具有含权边的连通无向图。G的一颗生成树(V,T)是G的作为树的子图。如给G加权并且T的各边的权的和为最小值,那么(V,T)就称为最小生成树。最小生成树的求解主要用到Prim和Kruskal算法。
3、简述贪心算法的思想,并列举一些贪心算法所解决的问题。
答:贪心算法的基本思想是找出整体当中每个小的局部的最优解,并且将所有的这些局部最优解合起来形成整体上的一个最优解。贪心算法解决的问题有:最短路径问题、最小生成树、文件压缩、货币兑换问题。
4、简述动态规划算法的思想,并列举一些动态规划算法所解决的问题。
答:动态规划的基本思想是问题的最优解如果可以由子问题的最优解推导得到,则可以先求解子问题的最优解,再构造原问题的最优解;若子问题有较多的重复出现,则可以自底向上从最终子问题向原问题逐步求解。动态规划解决的问题有:最长公共子序列问题、矩阵链相乘、背包问题。
5、假设两个大整数X,Y均为二进制数,传统的乘法算法需要O(n2)数字相乘来计算X和Y的乘积,若用分治算法可以使得时间复杂度减少为O(nlog3),简述此算法的思想。
答:
首先,采用分治算法,将X、Y分别拆分为A与B、C与D两个部分,此时X*Y可得:
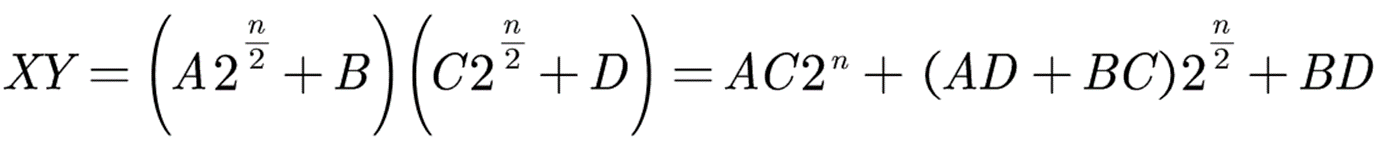
本式子中,有4次乘法运算,3次加法运算,可得出以下时间复杂度递推式:
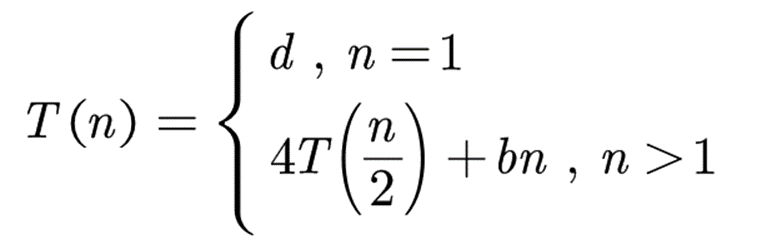
其中,b和d均为常数。
易得:
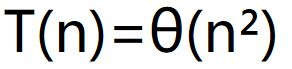
再次,运用加法来换取乘法,可以令:
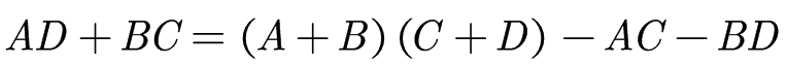
此时X*Y得:
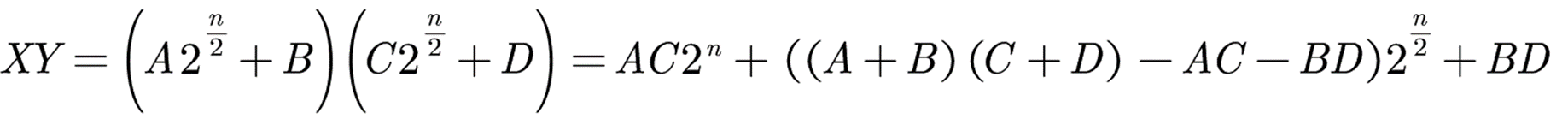
本式子中,有3次乘法运算,6次加法运算,可得出以下时间复杂度递推式:
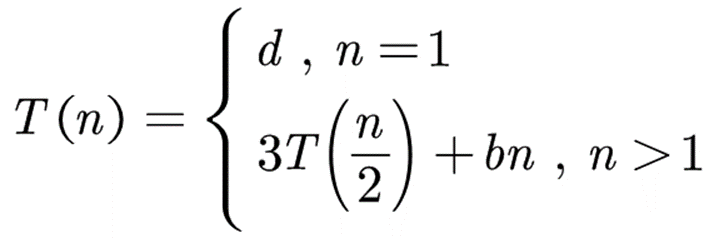
其中,b和d均为常数。
最后,易得:
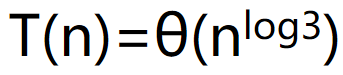
时间复杂度发生实质性变化。

 五个简答题
五个简答题

