算法设计与分析——分治递推关系的解
本节主要研究一些专门用来求解最常见的分治递推式的技巧。(代入法、更换变元法暂且不记录)
1、展开递推式
求解递推式的最自然方法就是通过显而易见的方式将其反复展开。
(1)、例子


O(n)取法:①忽略低阶项 ②舍最高项常系数 ③剩余估计
本例中,O(n)=nlog2 n
(2)、定理
由上例f(n)可得以下定理
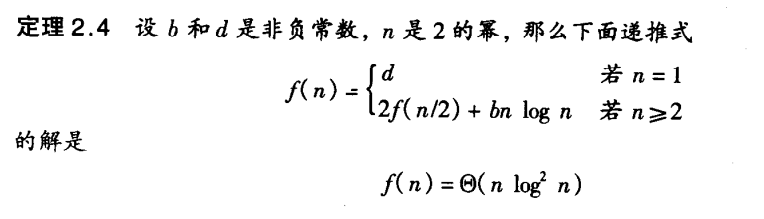
(3)、引理
对于不同的f(n),我们可以得出不同的递推式
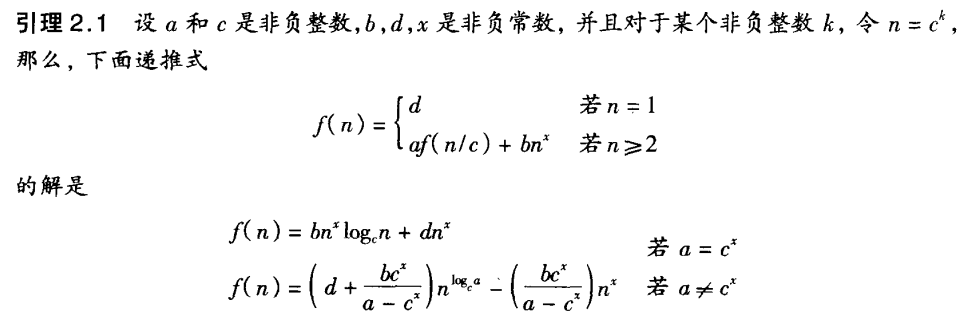
以上引理证明如下:


(4)、推论
由上述引理,我们可以得出以下两个推论
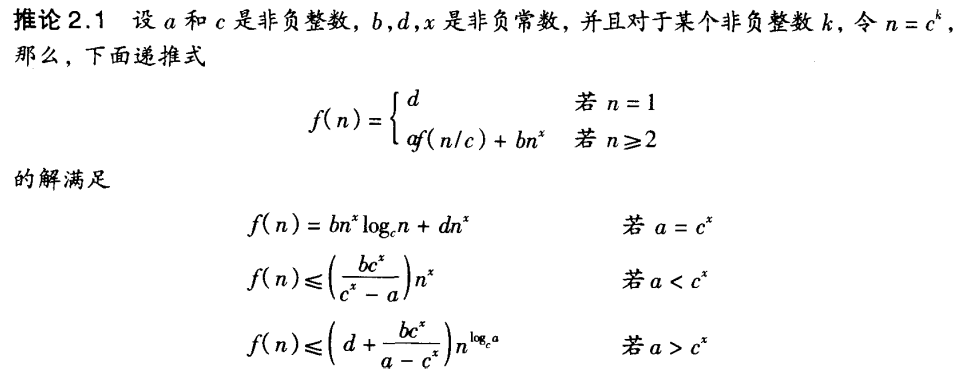
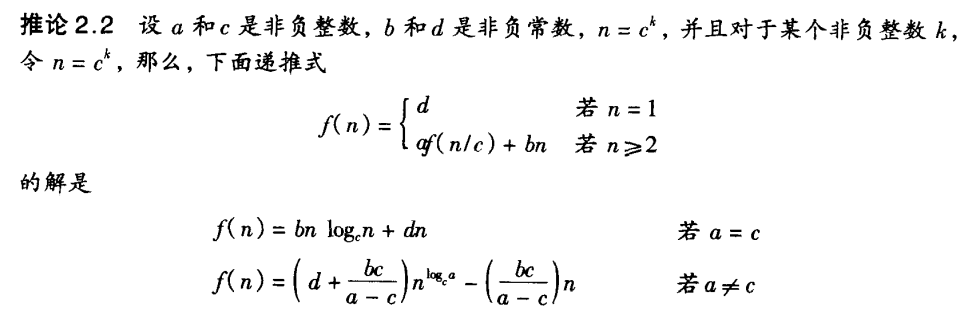
(5)、最重要的定理
背下该定理对于后期解题有很大帮助!

2、例题
(1)、例一

(a)

(b)
由master定理,a=4,c=2
显然,f(n)=O(n2),与展开递推式所得一致。
(2)、例二

(a)
求解法与例一一致。
(b)
由master定理,a=5,c=3
显然,f(n)=O(nlog35)。
(3)、例三
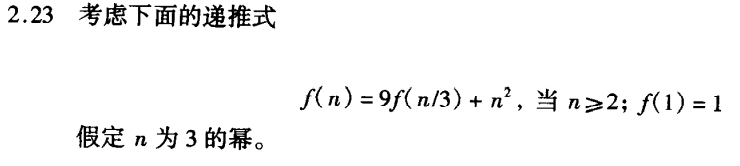
(a)
求解法与例一几乎一致。
(b)
由master定理,a=9,c=3,x=2
显然,f(n)=O(n2 log n)

 分治递推关系的解
分治递推关系的解

