算法设计与分析——动态规划之矩阵连乘
1、矩阵
首先,要了解什么是矩阵连乘问题,当然得先了解什么是矩阵了,学过线性代数的同学应该都知道,所以这里就简单的介绍一下什么是矩阵:
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合。例如:一个n*m的矩阵A=[a[i,j]]就是像下面一样的一个有着n行m列的二维数组:

2、矩阵连乘
学过线性代数的同学一定知道,一个p * q的矩阵A和一个q * r的矩阵B的乘积是一个新的p * r的矩阵C,即内积相同可乘。
举个简单例子:

3、矩阵连乘特点
- 如果存在两个矩阵A和B,如果AB能够计算乘积,则BA不一定能够计算乘积。
- 即使存在两个矩阵A和B,满足AB能够相乘,BA也能够相乘,但最后得出来的矩阵却很有可能是不一样的。
- 矩阵连乘可以被递归成如下形式:

- 矩阵连乘无论按照什么样的乘积顺序,最后计算出来的矩阵虽然“样子”不一样,但是计算出来的值却无论如何都是一样的。
4、矩阵连乘的复杂度分析
假设有一个p * q的矩阵A和q * r的矩阵B,则他们的乘积矩阵C=AB按照如下方式计算:

我们发现,矩阵C的规模应该为【p * r】,则矩阵C应该一共有【p * r】个实体并且每个实体需要【q】次的计算才能够算出来。因此,为了计算矩阵C的值,我们一共需要执行【p * q * r】这么多次计算。
因此,我们可以近似的认为矩阵连乘的复杂度就是矩阵连乘所需要的总次数,即O(p * q * r)。
5、矩阵连乘的计算次数与计算顺序的关系
假设有一个p * q规模的矩阵A,一个q * r规模的矩阵B,并且我们现在再加上一个规模为r * s的矩阵C,那么这三个矩阵的乘积ABC有两种计算顺序:
- (AB)C
- A(BC)
那么,肯定有同学要问了,这两种计算顺序有什么不同吗?无论采用哪种计算顺序他们的结果肯定都是一样的啊!那我们为什么要纠结它们的计算顺序呢?不是多此一举吗?
那就让我们来“探索”一下,这两种计算顺序有什么不同吧:
对于第一种计算顺序来说,总共需要的计算次数为:
因为AB共需要计算【p * q * r】次,并且生成一个规模为【p * r】的中间矩阵,这个中间矩阵再与矩阵C相乘,又需要计算【p * r * s】次,并且生成一个规模为【p * s】的矩阵,这个矩阵也就是最后的结果,因此,按照第一种顺序计算,一共需要的计算次数如下:
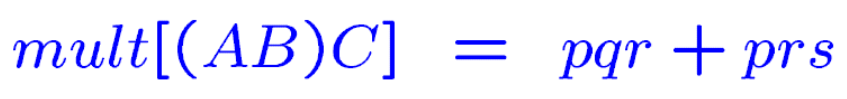
同理,按照第二种计算顺序,我们一共需要计算下面这么多次:

此时同学们注意了!!!好像两种计算顺序分别所需要的计算次数竟然是不一样的!!!那么,让我们把真实数据带入,来看一看差距有多大吧!
假设p=5,q=4,r=6并且s=2,则:

大的不同!按照第一种计算顺序,我们需要计算180次,而按照第二种计算顺序,我们只需要计算88次就够了!!!但是这两种顺序计算出来的矩阵的值却始终是一样的,真是太神奇了,计算顺序竟然能够影响所需要的计算次数,因此,对于矩阵连乘来说,计算顺序是非常重要的!
6、矩阵连乘问题
问题描述:
给你一系列的矩阵A1, A2, A3, ......,An和一系列的整数P0, P1, P2, ....., Pn,每个矩阵 Ai 的规模为Pi-1 * Pi。
现在,请你计算这些矩阵连乘所需要的最少的计算次数是多少?
针对这道题目,其实我们可以很清晰的认识到,需要找出最少的计算次数,就是需要我们找到“正确”的计算顺序!
此时肯定有同学会想到,我们可以使用暴力破解啊!循环算出所有可能的计算顺序的计算次数,然后取最小计算次数的那一个,就是我们需要的结果,例如,求A1A2A3A4,我们可以暴力循环出下面4种计算顺序来:

虽然这种方法确实也能够计算出最少计算次数,但是,我们知道暴力循环的复杂度是非常高的,如果我们需要计算的矩阵序列不止4个矩阵,而是很长的一串矩阵序列,那么将会非常的耗时,我们有这个时间计算最少计算次数,还不如随便找一个计算顺序直接算得了。暴力搜索的时间复杂度为:Ω(4n/n3/2)
难道,我们就只能用暴力算法了吗?当然不是,接下来就是我们的重头戏:DP(动态规划)了。
7、动态规划解决矩阵连乘
1️⃣ 找出最优子结构,在本问题中,即找出如何划分“括号”的方法。
首先,让我们把复杂的问题分解成子问题,对于每一对的 i 和 j ,都有1<=i<=j<=n,此时,我们只要确定了对于Ai..j=AiAi+1...Aj的乘积顺序,即如何“划分括号”,就决定了这一次乘积所需要的总计算次数。所以,我们只要找到一个乘积所需计算次数最小的计算顺序(打括号方式),就是我们的最优子结构。
特别的是,我们应该注意到,Ai...j的最后乘积结果是一个规模为【Pi-1*Pj】大小的矩阵。
我们前面讲了这么多,要想找到最少的计算次数,那么就必须要找到相对应的计算顺序,可是,计算顺序是一个抽象的东西,那么在我们这个问题里,计算顺序的具体体现是什么呢?
让我们这样来想,无论我们以一个什么样的乘法顺序来计算,最后一步都是一样的,即把最后生成的两个中间矩阵Ai...k和Ak+1...j相乘,其中k可以是在合法范围内的任意一个值:

让我们来举个例子:

此时,K=5,即应用该种计算顺序时,最后一步的乘积状态为A3...5*A6...6。
因此,决定最优乘积计算顺序的问题就可以分解为下面两个子问题:
- 我们应该在乘积序列中的哪一个地方使用大括号把该序列分成两个子序列呢?(即K的值到底应该设为多少?可以暴力列举出所有合法的K值)
- 对于分割出来的两个子乘积序列Ai...k和Ak+1..j,我们又该如何对他们再进行一步划分呢?
此时问题的“最优子结构”就已经出现了,为了保证Ai...k*Ak+1...j是最优的计算顺序,则Ai...k和AK+1...j也应该是由“最优计算顺序”计算出来的,因此,我们就可以递归的调用这个过程。
假设Ai...k的计算顺序并不是最优的,那么我们可以用更好的计算顺序去替换,这样就产生了悖论。
同样的,如果Ak+1...j并不是最优的,那么我们可以在找出另外一个更好的计算顺序来替换他,此时也产生了悖论。
2️⃣找出最优子结构的递推式。
就像我们学过的“0-1背包问题”一样,我们将会把“子问题”的解决方法储存到一个数组里头。
对于:1≤i≤j≤n
我们定义:m[i,j]的值为计算Ai...j所需要要的最少的计算次数,因此,这个最少计算次数的问题可以用下面的递归式来描述:

证明如下:

此时有些同学可能会疑惑,为什么最后还要加上1个Pi-1PkPj
因为根据我们前面的定义,Ai...k的乘积结果为一个规模为Pi-1 * Pk的矩阵,而Ak+1....Aj的乘积结果为一个规模为Pk * Pj的矩阵,所以,求Ai...j的最少乘积次数则为【Ai...k所需要的最少乘积次数】+【Ai+1...j所需要的最少乘积次数】+【中间生成的两个临时矩阵所需要的乘积次数】。
此时看似问题已经明朗了,但是!我们却并不能够确定K的值到底是多少?因为K的值不同,会造成序列的划分也不同,因此乘积次数也会不同,因此,我们只要找到某个K值,使得m[i,j]的值算出来是最小的,那么,我们的问题就迎刃而解了。
但是问题就是,咱们压根就不知道K值取啥啊?
不用急,既然咱们不知道K是啥,那就一个一个把K的可能值都代进去试一遍不就行了吗?而且K的可能值也只有j-i种,因此我们就把这j-i都一个个的去试一遍,然后找出m[i,j]最小的那一个情况,此时的K值就是我们需要的,并且最小乘积次数也找到了,就是m[i,j]次。
让我们再来看一看这个递推公式:

8、”自下而上“计算最优值
首先,让我们来回忆一下有关于二维数组m[i,j]的定义,m[i,j]的值为计算Ai...j所需要要的最少的计算次数。
因此,我们的二维表为m[1..n,1..n],并且有i<=j。
现在最关键的是:
当我们使用下面的等式:

来计算m[i,j]时,我们必须首先得把m[i,k]和m[k+1,j]计算出来,才能顺利把m[i,j]计算出来。
对于被分割的两个子序列,对应的矩阵链的长度都小于j-i+1。
因此,我们的算法以矩阵链长度增长的顺序来计算,就像下面这样子(假设我们需要计算m[1,n]):

9、动态规划时的注意事项
当我们设计一个动态规划算法时,我们需要注意下面两点:
1️⃣找到一个适当的最优子结构和在“表”中对应的循环关系,例如我们现在讨论的这个问题:

2️⃣找到“表”中各“元素”之间的某种关系。
例如,当我们需要计算表中某个位置的值时,我们要想一想,这个值是不是依赖了其他的值?是不是得先计算出其他的某个或几个值才能够计算出这个值来?
在我们现在这个例子中就是:
我们需要计算m[i,j]的值,但是计算这个值之前,我们必须得先计算:m[i,k]和m[k+1,j]两个元素的值。
10、样例解析
假设我们现在有4个矩阵A1,A2,A3,A4组成的一个矩阵链,并且各矩阵的规模用数组P[ ]表示,P0=5,P1=4,P2=6,P3=2,P4=7。
现在,需要你计算矩阵A1A2A3A4乘积所需要的最少的乘法次数,即求出m[1,4]的值。
解决方法:
使用动态规划算法解决,首先初始化数组m[i,j],为了便于同学们较为直观的观察数据的推导过程,数组m[i,j]我们不按照正常“表格”的方式展示,而是按照下面的“画法”来展示:

正如图中的标识一样,初始化时m[1,1],m[2,2],m[3,3],m[4,4]的值都为0,因为1个矩阵无法进行乘法运算,因此所需的计算次数当然为0了。
1️⃣步骤一
首先,计算m[1,2],即A1A2所需要的最少计算次数:
根据递推式有:

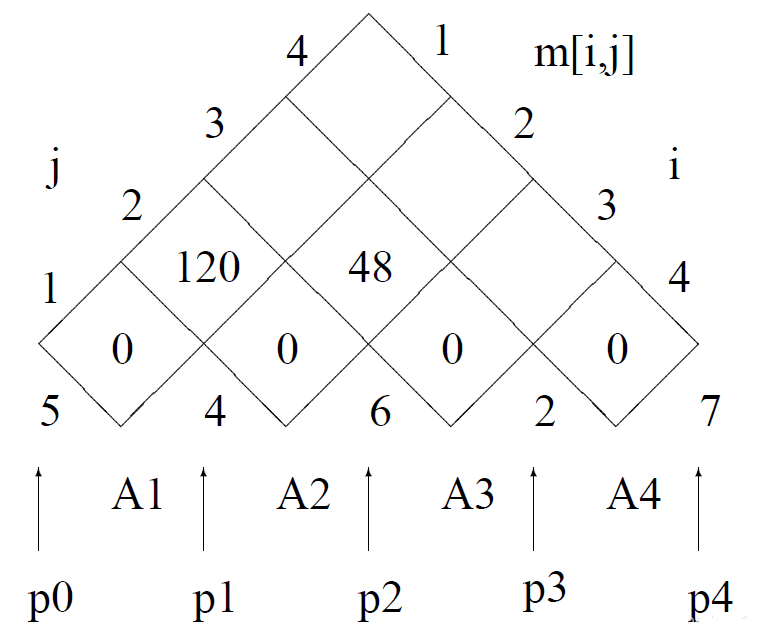
此时,K的取值范围只有1个合法值,即K=1。此时,A1A2的最少计算此时就是120次了,如下图所示:

2️⃣步骤二
根据定义,计算m[2,3]的值,根据递推式有:

此时,K的合法值也只有1个,即K=2,此时计算出来的值48就是A2A3所需要的最少计算次数啦!
3️⃣步骤三
计算m[3,4]的值,根据递推式有:

此时,K的合法值仍然只有1个,即K=3,此时计算出来的最小值为84。

4️⃣步骤四
计算m[1,3]的值,根据定义的递推式有:

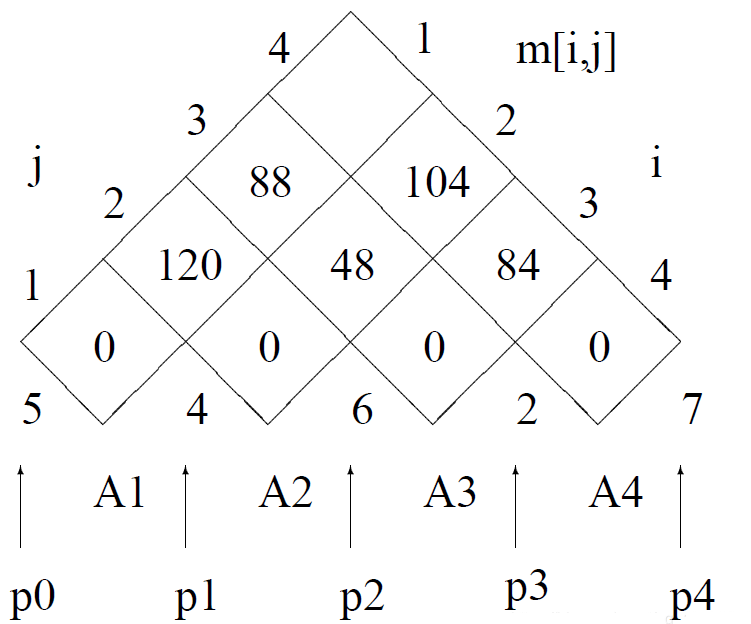
此时,K的合法值就有2个了,分别是1和2,也分别代表了两种“切割”序列的方法。通过找出这两种方法的最小值,即是此时最优的解啦!其实和上面的计算是一样的,只不过多了需要比较的一个情况而已。此时,我们的二维数组m如下图所示:

5️⃣步骤五
计算m[2,4]的值,根据定义有:

此时,K的合法值也有2个,也代表了A2..A4的两种“切割”方法。这两种“切割”方法所需要的计算次数的最小值为104,则这种方法是最优解,值也是最优值,即104。
6️⃣步骤六
计算m[1,4]的值,根据递推式有:

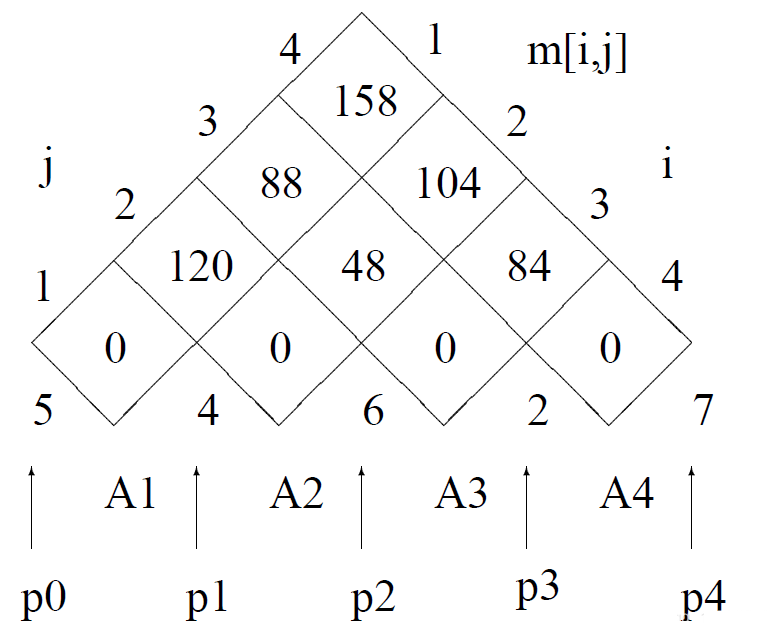
此时,K的合法值存在3种情况,分别为K=1,K=2,K=3,代表了3种“切割”方法,分别如下所示:
- A1(A2A3A4)
- (A1A2)(A3A4)
- (A1A2A3)A4
按照老样子,我们计算出m[1,4]的值为:158,即计算A1A2A3A4所需要的最少乘法次数为158次!

 通过矩阵连乘学习动态规划
通过矩阵连乘学习动态规划

