算法设计与分析——分治DC算法

1、Algorithm Introduction

（1）、Binary_Search

#include <stdio.h>
#define N 100

//子函数实现二分搜索算法，查找给定元素 x 的位置
int Binary_Search(int a[],int low,int high,int x)
{
	int mid;
	mid=(low+high)/2;
	if(low>high)
		return -1; /*查找失败*/
	else if(x==a[mid])
		return mid; /*找到元素的位置并返回*/
	else if(x>a[mid])
		return Binary_Search(a,mid+1,high,x);
	else
		return Binary_Search(a,low,mid-1,x);
}

void main()
{
	int a[N];
	int i,t,x,n;
	printf("请输入已排序数组中元素的个数 n:");
	scanf("%d",&n);
	printf("请输入已排序数组中的元素(共%d 个数):\n",n);
	for(i=0;i<n;i++)
	{
		scanf("%d",&a[i]); /*从键盘输入一组数*/
	}
	printf("请输入要查找的元素 x 为:");
	scanf("%d",&x);
	t=Binary_Search(a,0,n-1,x); /*调用子函数，查找元素 x 在数组 a[n]中的位置*/
	if (t==-1)
		printf("\n 查找失败!");
	else
		printf("元素 x 是数组中第%d 个元素。\n",t+1);  /*因为数组的下标从 0 开始，实际的位置应为其坐标位置加 1*/
}

（2）、Merge_Sort

#include <stdio.h>
#include <stdlib.h>
#define N 8

//将两个有序的数组 R[low...m]和 R[m+1...high]归并成一个有序的数组 R[low..high]
void Merge(int R[],int b[],int low,int m,int high)
{
	int i=low,j=m+1,p=0;
	while(i<=m&&j<=high) /*两子数组非空时取其小者输出到 R1[p]上*/
		b[p++]=(R[i]<=R[j])?R[i++]:R[j++];
	while(i<=m) /*若第 1 个子文件非空，则复制剩余记录到 R1 中*/
		b[p++]=R[i++];
	while(j<=high) /*若第 2 个子文件非空，则复制剩余记录到 R1 中*/
		b[p++]=R[j++];
	for(p=0,i=low;i<=high;p++,i++)
		R[i]=b[p]; /*归并完成后将结果复制回 R[low..high]*/
}
//用分治法对 R[low..high]进行二路归并排序
void MergeSort(int R[],int low,int high)
{
	int mid;
	int b[N];
	if(low<high) /*区间长度大于 1*/
	{
		mid=(low+high)/2; /*分解*/
		MergeSort(R,low,mid); /*递归地对 R[low..mid]排序*/
		MergeSort(R,mid+1,high); /*递归地对 R[mid+1..high]排序*/
		Merge(R,b,low,mid,high); /*组合,将两个有序区归并为一个有序区*/
	}
}

void main()
{
	int a[N];
	int i,j;
	for(j=0;j<N;j++)
		a[j]=rand()%100; /*系统随机生成 8 个数*/
	//scanf("%d",&array[j]); //取消此注释语句可以手动输入无序数组
	printf("随机生成数组为：\n");
	for(i=0;i<N;i++)
		printf("%d ",a[i]);
	MergeSort(a,0,N-1);
	printf("\n 已排序数组为：\n");
	for(i=0;i<N-1;i++)
		printf("%d ",a[i]);
	printf("\n\n");
}

2、Maximum Contiguous Subarray Problem

(1)、Overview

• Clean way to illustrate basic algorithm design
• • A Θ(n ³) brute force algorithm
  • A Θ(n ²) algorithm that reuses data
  • A Θ(n log n) divide-and-conquer algorithm
• Cost of algorithm will be number of primitive operations, e.g., comparisons and arithmetic operations, that it uses.

(2)、MCS Example

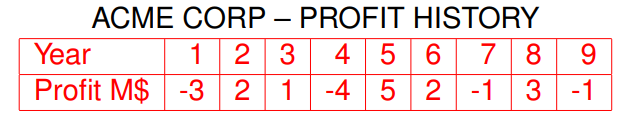
Between years 5 and 8 ACME earned 5 + 2 − 1 + 3 = 9 Million Dollars

This is the MAXIMUM amount that ACME earned in any contiguous span of years.

Examples: Between years 1 and 9 ACME earned −3 + 2 + 1 − 4 + 5 + 2 − 1 + 3 − 1 = 4 and between years 2 and 6 2 + 1 − 4 + 5 + 2 = 6

The Maximum Contiguous Subarray Problem is to find the span of years in which ACME earned the most, e.g., (5, 8).

(3)、Formal Definition

(4)、Θ(n ³) Solution: Brute Force

Idea: Calculate the value of V (i, j) for each pair i ≤ j and return the maximum value.

VMAX=A[1];
for (i=1 to N) 
{
	for (j=i to N) 
    {
		// calculate V(i, j)
		V=0;
		for (x= i to j)
			V=V+A[x];
		if (V > VMAX)
			VMAX=V;
	}
}
return VMAX;

(5)、Θ(n ²) Solution: Reuse data

Idea: We don’t need to calculate each V (i, j) from “scratch” but can exploit the fact that

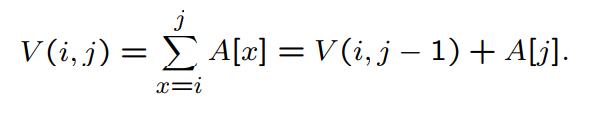
VMAX=A[1];
for (i=1 to N)
{
	V=0;
	for (j=i to N) 
    {
		// calculate V(i, j)
		V=V+A[j];
		if (V > VMAX)
		VMAX=V;
	}
}
return VMAX;

(6)、Θ(n log n) Solution: Divide-and-Conquer

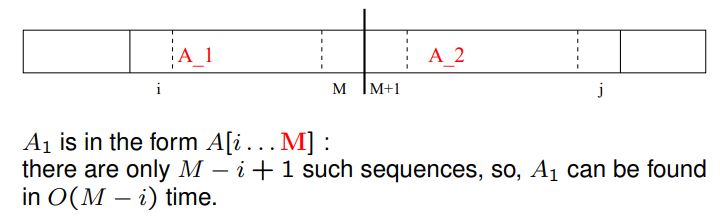
Idea: Set M = [(N + 1)/2] , [] indicates rounding down temporarily.

Let A₁ and A₂ be the MCS that must contain A[M] and A[M + 1] respectively. Note that the MCS must be one of

• S₁ : The MCS in A[1 . . . M]
• S₂ : The MCS in A[M + 1 . . . N]
• A : Where A = A₁ ∪ A₂

(7)、Example

(8)、Finding A : The conquer stage

MAX=A[M];
SUM=A[M];
for (k=M-1 down to i)
{
	SUM+=A[k];
	if (SUM > MAX) 
        MAX=SUM;
}
A_1=MAX;

(9)、The Full Divide-and-Conquer Algorithm

// Input : A[i . . . j] with i ≤ j

// Output : the MCS of A[i . . . j]

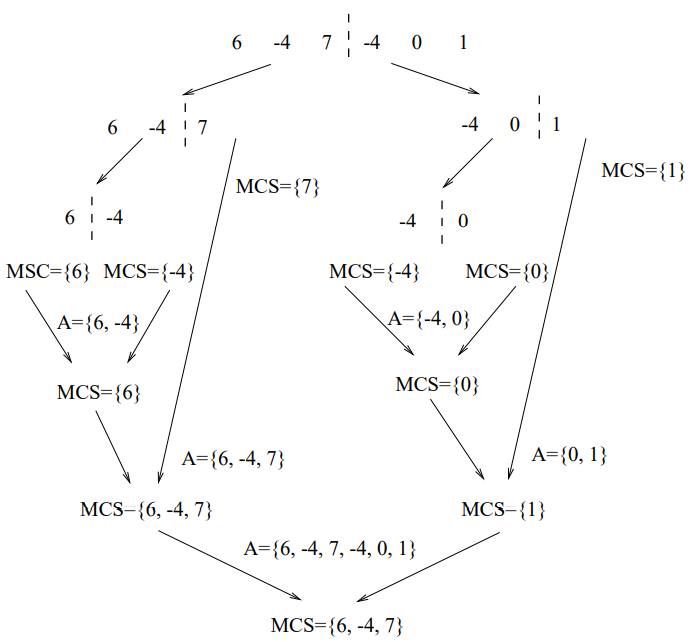
(10)、A full example

(11)、Analysis of the DC Algorithm

Let T(m) (where m is the problem size) be time needed to run

​ MCS(A, i, j), (j − i + 1 = m)

Step (1) requires O(1) time.

Steps (3) and (4) each require T(m/2) time.

Step (5) requires O(m) time.

Step (6) requires O(1) time

Then T(1) = O(1) and for n > 1, T(n) = 2 T(n/2) + O(n)

To simplify the analysis, we assume that n is a power of 2.

T(n) ≤ 2 T( n 2 ) + c n.

Repeating this recurrence gives

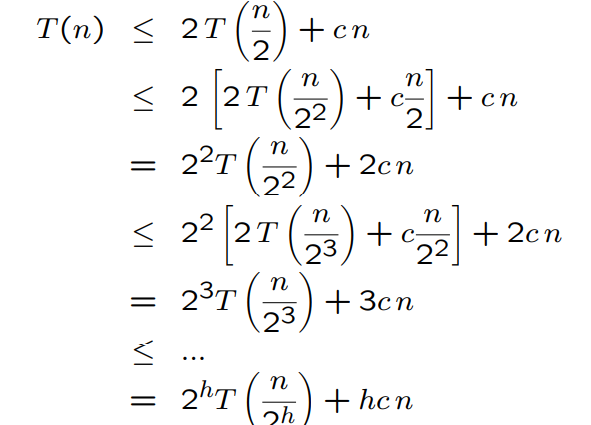
Set h = log₂ n, so that 2 ^h = n.

With this substitution, we have

(12)、Review

In this lecture we saw 3 different algorithms for solving the maximum contiguous subarray problem. They were

• A Θ(n ³) brute force algorithm
• A Θ(n ²) algorithm that reuses data
• A Θ(n log n) divide-and-conquer algorithm