算法设计与分析——Introduction
1、Computational Problems and Algorithms
-
Definition: A computational problem is a specification of the desired input-output relationship.
-
Definition: An instance of a problem is all the inputs needed to compute a solution to the problem.
-
Definition: An algorithm is a well defined computational procedure that transforms inputs into outputs, achieving the desired input-output relationship.
-
Definition: A correct algorithm halts with the correct output for every input instance. We can then say that the algorithm solves the problem.
2、Example of Problems and Instances

3、Example of Algorithm : Insertion Sort
In-Place means 就地

4、Insertion Sort: an Incremental Approach

5、Analyzing Algorithms

依赖于计算模型(顺序or并行,一般取顺序,即单处理器)

6、Three Cases of Analysis

7、Three Analyses of Insertion Sorting
- Best:
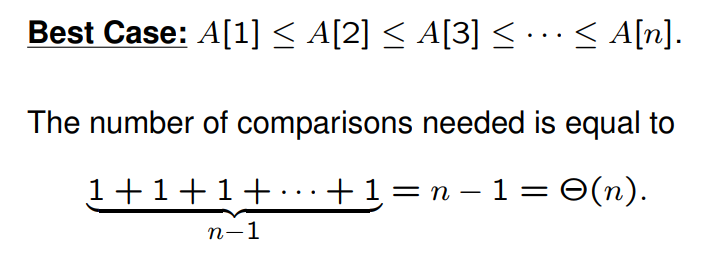
- Worst:
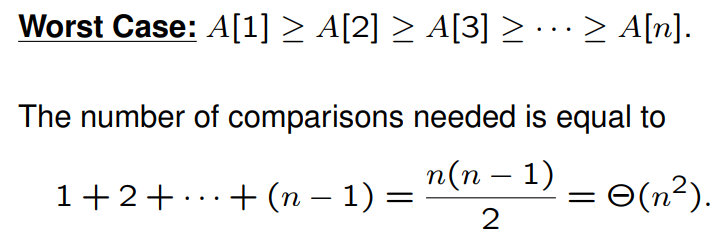
- Average:
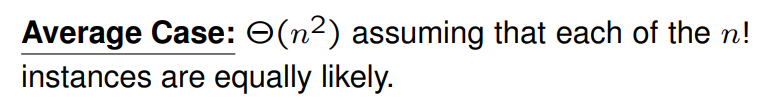
8、Asymptotic Time Complexity Analysis
- We would like to compare efficiencies of different algorithms for the same problem, instead of different programs or implementations. This removes dependency on machines and programming skill.
- It becomes meaningless to measure absolute time since we do not have a particular machine in mind. Instead, we measure the number of steps. We call this the time complexity or running time and denote it by T(n).
- We would like to estimate how T(n) varies with the input size n.
9、Big-Oh
If A is a much better algorithm than B, then it is not necessary to calculate TA(n) and TB(n) exactly. As n increases, since TB(n) will grow much more rapidly, TA(n) will always be less than TB(n) for large enough n.
Thus, it suffices to measure the growth rate of time complexity to get a rough comparison.
f(n) = O(g(n)):
There exists constant c > 0 and n0 such that f(n) ≤ c · g(n) for n ≥ n0.
When estimating the growth rate of T(n) using big-Oh:
- Ignore the low order terms.
- Ignore the constant coefficient of the most significant term.
- The remaining term is the estimate
For example,
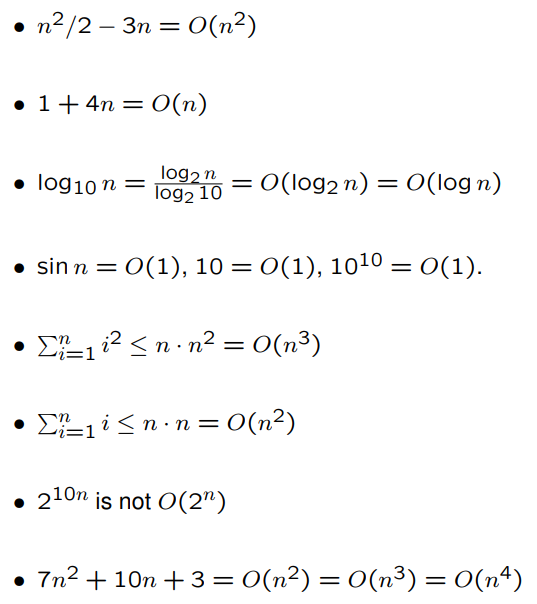
10、Big Omega and Big Theta
f(n) = Ω(g(n)) (big-Omega):
There exists constant c > 0 and n0 such that f(n) ≥ c · g(n) for n ≥ n0.
f(n) = Θ(g(n)) (big-Theta):
f(n) = O(g(n)) and f(n) = Ω(g(n)).
11、Some thoughts on Algorithm Design
- Algorithm Design, as taught in this class, is mainly about designing algorithms that have small big-Oh running times.
- “All other things being equal”, O(n log n) algorithms will run more quickly than O(n 2) ones and O(n) algorithms will beat O(n log n) ones.
- Being able to do good algorithm design lets you identify the hard parts of your problem and deal with them effectively.
- Too often, programmers try to solve problems using brute force techniques and end up with slow complicated code! A few hours of abstract thought devoted to algorithm design could have speeded up the solution substantially and simplified it.
Computer A(faster, 1010 instructions/second ), insertion sort, T1(n) = c1 O(n 2)
Computer B(slower, 107 instructions/second), merge sort, T2(n) = c2 O(n log n)
suppose n = 107 , c1 = 2, c2 = 50

We should consider algorithms, like computer hardware, as a technology. Total system performance depends on choosing efficient algorithms as much as on choosing fast hardware.

 对算法的简单介绍
对算法的简单介绍

