并行多核体系结构基础——第六章知识点和课后习题

第五章讨论了单处理器的存储层次组织和并行多核系统，本章将讨论需要什么样的硬件支持才能保证在多处理器系统上基于共享存储的并行程序的正确执行。

本章节主要介绍三点内容，分别是：

①缓存一致性问题：确保多个处理器看到的缓存数据是一致的。

②存储一致性问题：确保存储操作顺序在不同处理器上是一致的。

③同步问题：提供一个简单、正确和高效的原语来支持程序员控制并行程序。

知识点：

6.1缓存一致性问题

假设一个多处理器系统，每个处理器都有一个私有高速缓存，并且将这些处理器聚合在一起形成基于共享存储的多处理器系统。假设通过总线将这些处理器互连在一起，如下图所示：

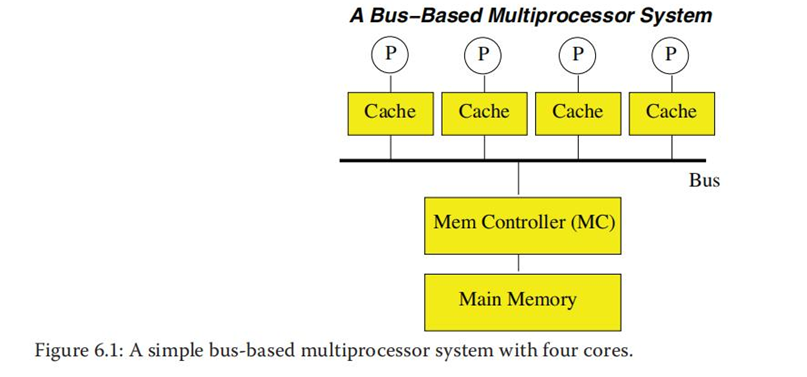
两个线程在两个处理器上执行来累加和：

# 代码 累加两个值到sum中
sum = 0;
# pragma omp parallel for
for (i=0; i<2; i++) (
     #pragma omp critical{
     sum = sum + a[i];
    }
 }
 ... = sum;

假设a[0] = 3并且a[1] = 7。计算的正确结果是在计算结束时sum中包含了 a[0]和a[1] 之和，其值等于10。假设已经插入了合适的同步语句从而每次只能有一个线程访问sum。在没有高速缓存的系统中，线程0从存储中读取sum的初始值，累加3到sum中，并将结果存回存储。线程1从存储中读取sum的值（这时已经是3）,累加7到sum中，并将结果10存回存储。当线程0下一次从存储中读取sum时，这时的值已经是10,该结果正确。（这是我们期望的结果）

现在想象每个处理器都有一个高速缓存（见上图6.1）,更具体点，该高速缓存为写回髙速缓存。初始化时，存储中sum的值为0。操作的顺序如下表所示。线程0开始从存储中变量sum的地址读取（load指令）数值进入寄存器，这就导致包含sum的存储块被缓存到处理器0中。之后，线程0执行加指令将sum与a[0]相加。相加的结果当前仍然保存在寄存器中，之后通过store指令写回sum在存储中的地址。由于包含sum的存储块已经被缓存，缓存块修改后脏位会被设置。同时，主存中仍然保存着已经过时的存储块，其中sum的值为0。当线程1从主存中读取sum时，它将看到sum的值为0。然后将a[1]和sum相加，并将结果存在高速缓存中，其缓存的sum值为7。最终，当线程0读取sum的值时，将会直接读取其缓存中的有效副本（缓存命中），那么它得到的sum的值为3,这是不正确的。

我们可能会考虑是否将写回高速缓存替换为写直达高速缓存问题就能得到解决。答案是否定的。如表6-1所示的序列，采用写直达高速缓存可以部分缓解该问题，因为当线程0更新sum时，该更新会被传播到主存中。因此，当线程1读取sum的值时，它将读到正确的值3。之后线程1将sum与7相加，这时sum变为10。当更新sum的值时，同时会被传播到主存中。因此，主存中sum的值为10。然而，当线程0打印sum的值时，会发现处理器0的高速缓存内已有sum的有效副本（缓存命中），那么其打印岀来的值是3 （尽管事实上主存中的sum具有最新值10 ）,这是不正确的。

整体上讲，高速缓存的写策略（写直达或者写回）只能控制高速缓存副本值的修改如何被传播到外层高速缓存层次（如主存），但并不能控制缓存副本值的修改如何被传播到同级高速缓存的其他副本中。当然，这个问题对于没有高速缓存的系统并不存在。由于该问题的根源在于同一个数据在不同高速缓存中看到的值是不一致的，因此也被称为缓存一致性问题。

为了满足数据在多个高速缓存中具有相同的值，需要缓存一致性的支持，至少需要一个机制来将一个高速缓存中的修改传播到其他高速缓存中。这种需求被称为写传播需求。支持缓存一致性的另一个需求是事务串行化。事务串行化本质上要求对于同一存储地址的多个操作，在所有处理器看来其顺序是一致的。

①事物串行化的需求

首先讨论两个写之间的串行化需求，之后再讨论一个读和一个写之间的串行化需求。1）两个写之间的串行化需求，如图（a）所示。图中假设有4个处理器：P1、P2、 P3和P4。 P1在其高速缓存中x的地址上写入值1,与此同时P2在其高速缓存中相同x的地址上写入值2。如果只提供写传播而没有串行化，P3和P4可能会看到对x的不同修改顺序。 P3可能看到P2的写入发生在P1的写入之前，因此它看到的x的最终值是1。相反，P4可能看到P1的写入发生在P2的写入之前，因此它看到的x的最终值是2。最终，P3和P4对于相同的存储地址看到不同的值，这就是缓存数据发生不一致。因此，需要在写之间进行串行化，从而保证所有处理器看到的缓存数据是一致的。

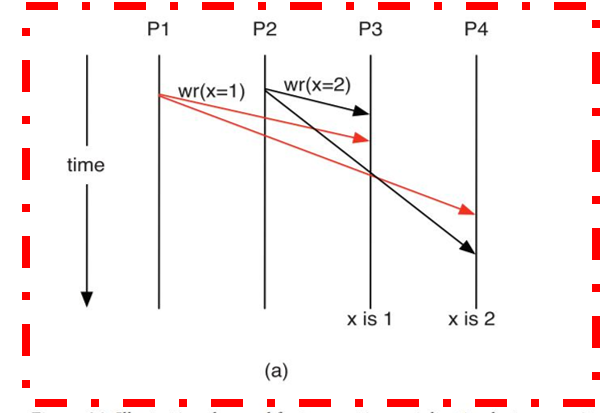
②读写之间需要进行串行化

图（b）所示。图中假设有3个处理器：P1、P2和P3。P1 在其高速缓存中的x地址上写入值1,该更新在不同的时间内被传播到P2和P3。如果只提供了写的串行化而没有提供读写之间的串行化，对于x，P2和P3可能会看到不同的值。假设 P2执行了读操作并将其转发给P3。P3还没有收到从P1发过来的写传播，因此将x的旧值0返回给P2。最终，P3收到从P1发过来的写传播，并将x的值更新为1。最终，P2认为x的最新值为0,而P3认为x的最新值为1。P2和P3对于相同的存储地址看到了不同的值，这就是缓存数据发生不一致。因此，需要在读写之间进行串行化，从而保证所有处理器看到的缓存数据是一致的。

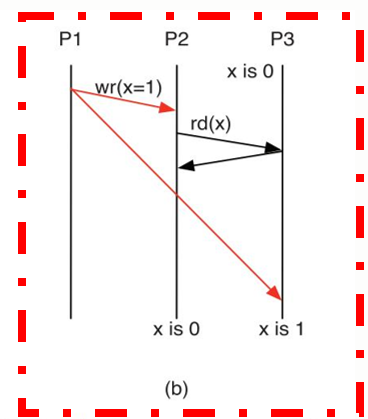
缓存一致性是通过被称为缓存一致性协议的机制来实现的。为了保证缓存一致性协议的正确性，需要实现写传播和事务串行化。

6.2存储一致性问题

缓存一致性需要将同一地址上的值的修改从一个高速缓存中传播到其他高速缓存，并且将这些修改串行化。

存储一致性主要用于解决对不同存储地址的所有存储操作 （load和store）的排序。该问题被称为存储一致性，因为不像缓存一致性问题只发生在有高速缓存的系统中，即使在没有高速缓存的系统也存在存储一致性问题，尽管高速缓存可能使得该问题更加严重。

为了解释这个问题,考虑一组信号-等待同步。假设线程0产生了一个数据，而该数据将会被线程1所使用（读）。线程0执行post函数通知线程1数据已经准备好，线程1执行wait函数阻塞等待直到相应的post函数被执行。一种实现信号-等待对的简单方法是使用初始化为0的共享变量。post操作将该变量设置为1,而wait操作等待直到该变量被设置为1。该方法如下代码所示。在该代码中，共享变量datumlsReady实现了信号一等待对。 处理器1 （执行线程1 ）在循环中等待直到datumlsReady被设置为1,这也意味着datum已经产生。

考虑上述代码在单处理器系统上是否可以正常运行。在单处理器系统上，代码执行的正确性取决于S1语句是否在S2语句之前被执行。如果基于一些原因语句S2在S1之前被执行，那么datumlsReady在datum被写入之前被设置为1。类似地，如果S4在S3之前被执行，它可能在datum被写入之前执行了打印操作。因此，代码执行的正确性取决于SI、S2、 S3和S4语句执行的合适顺序。与源程序对应的二进制代码保留语句原有的执行顺序至关重要。程序源码中呈现出的指令顺序被称为程序顺序。

首先考虑S3和S4的程序顺序是如何在单处理器上得到保留的。当今的典型处理器都实现了乱序执行机制，该机制可能会对指令的执行重新排序从而发掘指令级并行，并且仍然保留依赖（数据和控制流）和指令提交的程序顺序。S4的执行依赖于S3中的循环条件是否满足，因此S3与S4之间存在控制流依赖。因此处理器遵循控制流依赖，S3和S4将按照程序顺序执行。

接着考虑S1和S2。S1和S2中的store指令既不存在数据依赖（真依赖、反依赖或者输出依赖），又不存在控制流依赖。在执行过程中，S2可能在S1之前被执行，但是由于单处理器实现了顺序指令提交，这就保证了与S1相关的指令总是在S2之前被提交。因此，除非二进制代码本身没有保留程序顺序，否则代码将会正确执行。这里需要提供一个方法来告诉编译器在产生二进制代码时保留程序顺序。告诉编译器保留程序顺序的典型做法是提供编译器可以理解的语言结构。其中的一个例子就是在C/C++中，如果将datumlsReady声明为 volatile类型，编译器就会知道对该变量进行的load或者store操作不能被移除，也不能与其之前和之后的指令调换顺序。虽然上述方法可能对于程序顺序的要求过于严格（并不是所有关于volatile变量的load和store指令都需要严格按照程序顺序），但它使用起来比较简单。 程序员只需要记得哪些变量需要用于同步，并将其声明为volatile变量。

整体上讲，在单处理器系统中，为了代码的正确执行，只需要让编译器对访问同步变量的指令保留程序顺序。

6.3同步问题

即使有缓存一致性支持，下述代码中的例子假设 “#pragma omp critical"子句所需的同步原语已经在系统上实现。现在的问题是临界区所需的互斥如何实现。互斥要求当有多个线程访问时，在任何时间内只有一个线程可以访问临界区。

# 代码 累加两个值到sum中
sum = 0;
# pragma omp parallel for
for (i=0; i<2; i++) (
     #pragma omp critical{
     sum = sum + a[i];
    }
 }
 ... = sum;

互斥并不是多处理器系统中的特殊问题。在单处理器系统上，如多个线程共享一个处理器，并对可能被多个线程修改的变量进行访问时，需要使用临界区进行保护。一个暴力实现临界区的方法就是针对需要互斥的代码段关闭中断。关闭所有的中断可以保证线程的执行不会被操作系统上下文切换或者中断。这种方法对于单处理器系统而言代价较大。在多处理器系统中，除了开销较大，关闭中断也无法实现排他访问，因为在不同处理器上的其他线程仍然可以同时执行。

为了实现互斥，假设已经实现了lock (lockvar)原语，该原语可以获得锁变量lockvar, 并通过unlock (lockvar)原语释放锁变量lockvar。同时假设lockvar在被一个线程获取时值变为1,否则其值为0。为了进入临界区，这些函数的一个简单实现如下面代码所示：

代码展示了为了获得锁，线程需要进入循环以等待lockvar的值变为0,也就意味着该锁已经被释放。之后，线程获得锁并将lockvar置为1,这将在线程成功获取锁之后防止其他线程进入临界区。最后，当线程离开临界区时，将lockvar重置为0。简单实现的问题在于读取lockvar变量值和写入lockvar变量值的指令序列不是原子的， 特别是在相应的汇编语言中可以看出。读取lockvar值和写入lockvar值是不同的指令，并且在这些指令之间还有其他指令，如比较和分支指令。这些指令序列不是原子的，因为指令序列执行的中间可能会被中断，并且可能与其他处理器上运行着的相同指令序列相互重叠。这种非原子性会允许多个线程读取lockvar并获得相同的值，如0,这就意味着多个线程可以同时获取该锁，从而导致正确性问题。

解决该问题的一个方法是引入原子指令的支持，原子指令可以将读、修改和写的指令序列作为一个不可分割的单元来执行。这里的原子指令暗含着两个意思。首先，它意味着要么整个指令序列得到完整执行，要么该指令序列中没有一个指令得到执行。其次，它也意味着在任意时间点以及无论哪个处理器上，该指令序列中都只有一个指令得到执行。如何实现原子指令呢？当然，软件支持无法提供指令的原子执行。因此，需要相应的硬件支持。

本章将从另一角度来看待硬件支持的必要性，即是否存在一个方法不需要硬件支持？如果有，该方法是否高效？为了回答这个问题，考虑通过软件方法实现互斥，如Peterson算法。Peterson算法通过下述代码在两个线程间实现了互斥。

工作原理：

首先，代码退出while循环并且成功获得锁的条件为：要么turn不等于process,要么interested[other]值为FALSE。当只有一个线程尝试着获取锁时，因为interested[other]值为FALSE,它将成功获取锁。当线程退出临界区时， 只需要将interested[other]值置为FALSE,从而其他线程可以进入临界区。

虽然软件方法（Peterson算法）也可以实现互斥，但该方法可扩展性较差。

最后需要注意，同步原语的正确性与处理器提供的存储一致性模型紧密相关。本质上，同步操作用于对不同线程的存储访问进行排序。然而，同步操作无法保证由其排序后的存储访问与未由同步操作排序的存储访问之间的顺序，除非硬件要么提供一个严格的存储一致性模型，要么提供一个明确的机制来对存储访问进行排序。

课堂习题：

习题1

习题2

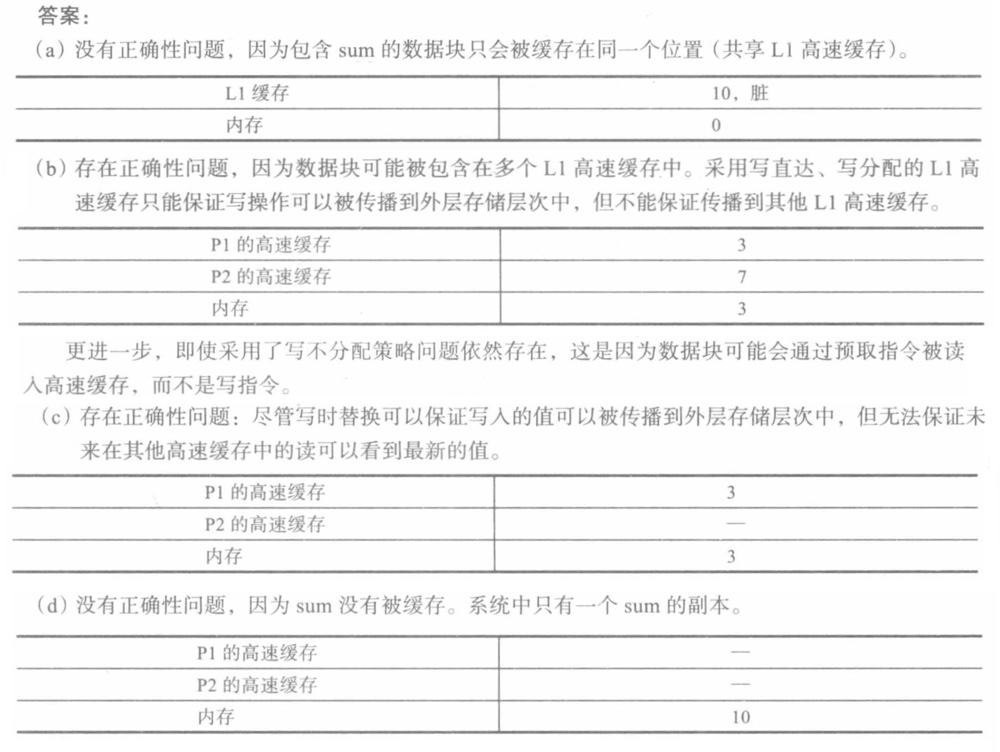
课后习题：

习题1

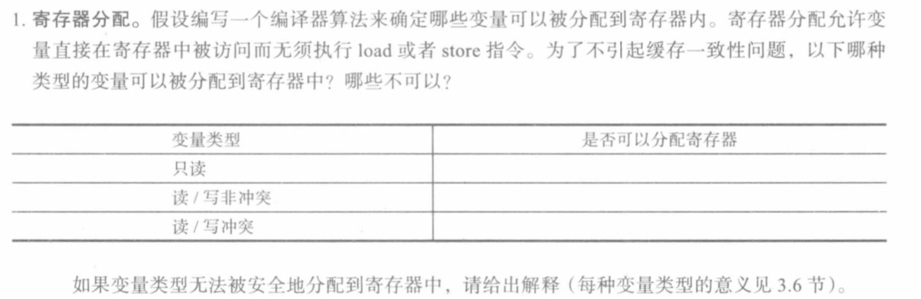
读写冲突的变量由不同的任务读写，所以不能分配在寄存器中。处理器核在寄存器上的操作是独立的，所以容易造成数据错误。

习题2

（a）

会有确定性问题。因为数据存在两个 L1 缓存和一个 L2 缓存中写会策略只可以将内层数据传递到外层，无法在多个 L1 之间传播。

（b）

不会有确定性问题。因为数据不能同时被两个缓存存储 当其中一个缓存读取数据，另一个缓存只能丢失这个数据，并且下一次读取时为最新的值。

（c）

会有确定性问题。时间片轮转 T1 先读取数据块缺失预取到 L1，T2 执行读取内存 中 sum 的值并且放入 L2 ，T1 读取 sum 的值 ，T2 执行 sum+=7 ，写回内存 ，T1 执行 sum+=3， 写回内存 ，覆盖了 T2 的数据， 所以会有确定性问题。

（d）

会有确定性问题。 P1 的 L1 的数据为脏数据，因为是写回策略 L1，L2 之间不会同意数据。

习题3

Peterson算法在2个线程间的实现：

int turn;
int interested[n]; //被初始化为0

void lock(int process) //process为0或1
{
    int other = 1 - process;
    interested[process]  = TRUE;
    turn = process;
    while(turn == process && interested[other] == TRUE) {};
}

void unlock(int process)
{
    interested[process] = FALSE;
}

Peterson算法在4个线程间的实现：

int turn;
int turnGroup;
int interested[n];
int interestedGroup[n/2];

void lock( int process)
{
	// 判断是那一组
	int group = process%2;
	int otherGroup = 1 - group;
	interestedGroupt[group] = TRUE;
	turnGroup = group;
	// 组竞争锁
	while (turnGroup == group && interestedGroup[otherGroup] == TRUE){}
	// 组内竞争
	int other = (process+2)%4;
	interested[other] = true;
	turn = process;
	while (turn == process && interested[other] == TRUE){}
}

void unlock(int process)
{
	int group = process%2;
	interestedGroupt[group] = FALSE;
	interested[process] = FALSE;
}