并行多核体系结构基础——第四章知识点和课后习题
本章节主要介绍链式数据结构(Linked Data Structure,LDS)下的并行编程。
知识点:
4.1 LDS并行化所面临的挑战
链式数据结构包含不同类型的数据结构,如链表、树、散列表和图等。 所有链式数据结构的共同特点是都包含一组节点并且节点之间通过指针相互链接。指针是存放地址的一种数据类型。就构造一个单向链表(单链表)来说,每一个节点都包含一个指向链表中下一个节点的指针。对于双向链表,每一个节点包含两个指针,分别指向该节点的前一个节点和后一个节点。树具有层次化结构,其根节点在最高层,叶子节点在最底层。树结构中的节点包含指向子节点的指针,有的还包含指向父节点的指针。图结构由一个节点集合构成,其中每一个节点都可以指向其余的任意节点,并且其指向其余节点的指针数可以是任意的。
虽然不同链式数据结构之间存在差异,然而链式数据结构的遍历都具有一个相同的特征,即在遍历过程中需要读取当前节点中的指针以发现该指针指向的下一个节点,并以此方法访问所有节点。因此,不同于矩阵遍历(其中矩阵的索引可以通过算术计算获得),LDS在遍历过程中需要读取到当前节点的指针数据才能获得下一个节点的地址。这样的模式导致链式数据结构的遍历过程存在循环传递依赖-循环级并行化的不足。
循环传递依赖不仅仅存在于遍历语句中,还有特殊情况。例如,LDS本身包含环路,也就是从当前节点出发向后遍历会再次回到该节点。这种情况常见于图中,但也有可能发生在链表中(循环链表)。
LDS并行化面临的另一个问题则来自递归遍历。例如,对于树的遍历往往就会用到递归。递归遍历并不是并行化的主要障碍。例如,在遍历树时,可以创建两个线程分别遍历左子树和右子树。这样,就能够从某种程度上将树的递归遍历并行化。然而,这种方法只对特定数据结构有效。
由于循环传递依赖的存在,并行化LDS的遍历过程变得困难。
4.2 LDS并行化技术
(1)计算并行化与遍历
一个简单的并行化LDS的方法是将其计算部分并行化(而非遍历过程)。 假设程序需要遍历链表并在每个节点上执行计算操作,循环传递依赖只会影响节点的遍历而非计算操作。 因此,可以在保持遍历过程串行执行的基础上,将每个节点上的计算操作分配到不同的任务上并行执行。该方法如下:
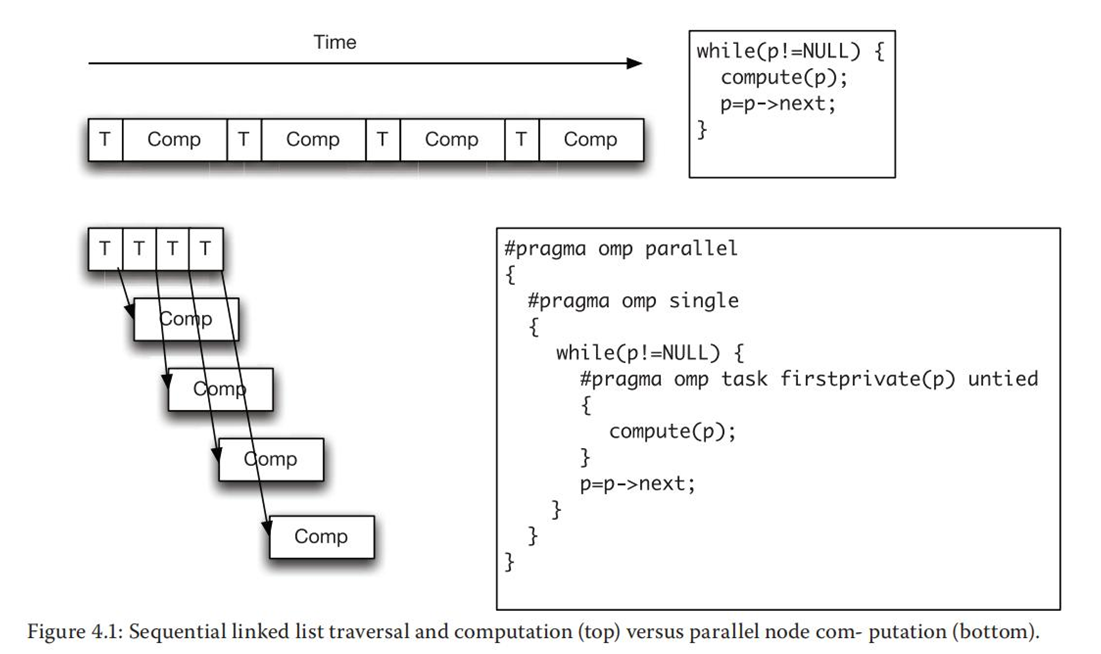
总的来说,这个方法比较直观且相对容易实现。然而,如果考虑到该方法的执行效率,预取操作可以进一步提升该方法的性能。
如果多个线程共享处理器上的高速缓存,主线程在遍历LDS的过程中会将节点上的数据预取到共享高速缓存中,这样便可以减少程序运行过程中从线程的缓存缺失次数。
然而相较于执行遍历和任务管理所耗费的时间比重,真正影响该方法性能的因素是执行节点计算操作的时间。当需要处理大量的任务时任务管理的开销就会显著增加。假设执行计算操作的时间等于或小于遍历时间与任务管理时间之和,则该方法能获取的最大加速比为2。可以将遍历时间和任务管理时间看作Amdahl定律中的串行部分,该部分会决定可以获得的最大加速比。为了在线程数量增加时获取较高的加速比,需要执行计算操作的时间远远大于遍历时间与任务管理时间之和。
(2)针对数据结构的操作并行化
另一个LDS并行化方法是对LDS的操作进行并行化。从算法层面上来看,可以将LDS当作支持一系列基本操作的数据结构,比如插入节点、删除节点、搜索节点以及修改节点等操作。对于某些LDS,可能还有其他基本操作,比如对树LDS进行平衡操作。
如果想要并行执行不同的操作,就必须选用恰当的方法来实现并行。也就是说,并行执行的结果必须要与串行执行的结果一致。严格来说,这种约束是在可串行性概念中定义的,该概念指明“一组并行执行的操作或者原语是可串行化的,如果其所产生的结果与某串行执行情况下所产生的结果相同”。
例如,假设一个程序将插入节点和删除节点的操作并行执行, 如果其最后的执行结果与先执行插入操作然后执行删除操作,或者先执行删除操作然后执行插入操作的串行方式的结果一致,那么它就具有可串行性。
确保LDS的操作能正确并行执行的关键是并行执行的结果永远与串行执行的结果一致。
综上,并行化LDS操作所面临的挑战:
①当针对同一节点的两个操作并行执行时,如果其中有至少一个操作会修改节点值,就会产生冲突并导致不可串行化结果。值得注意的是,如果两个操作影响的是完全不同的节点集合,那么将不会导致冲突。
②在要点①出现冲突的情况下,某些时候仍然可能出现可串行化结果。在前面通过删除节点和搜索节点操作并行执行仍然可以得到可串行结果的例子说明了这一点。不幸的是,这种情况只适用于特定场景,不适用于所有类型的LDS。
③在LDS操作与内存管理函数(如内存回收及分配)之间也会出现冲突。之前讨论过,即使删除节点和搜索节点可以并行执行,仍然需要确保搜索到的节点内容没有被节点内存回收程序所损坏。
举几个栗子:
①两个插入操作并行执行产生不可串行化的结果:
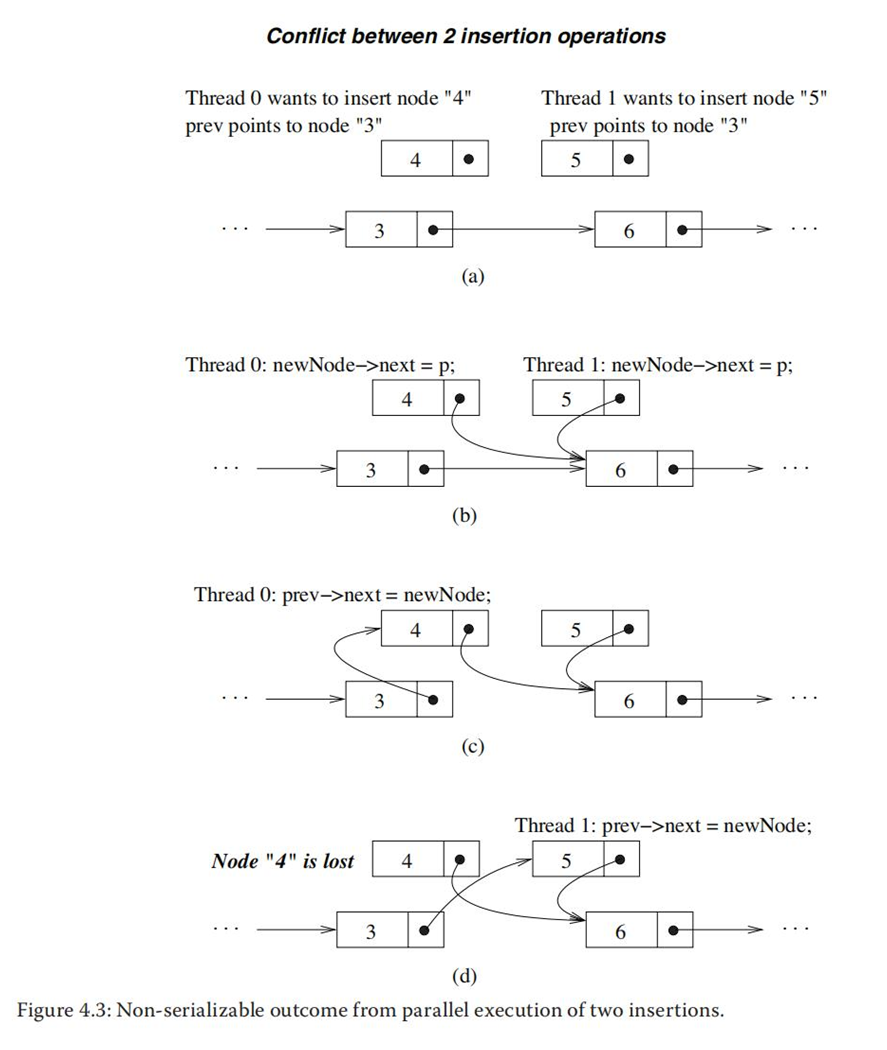
②一个插入和一个删除操作并行执行产生不可串行化结果:
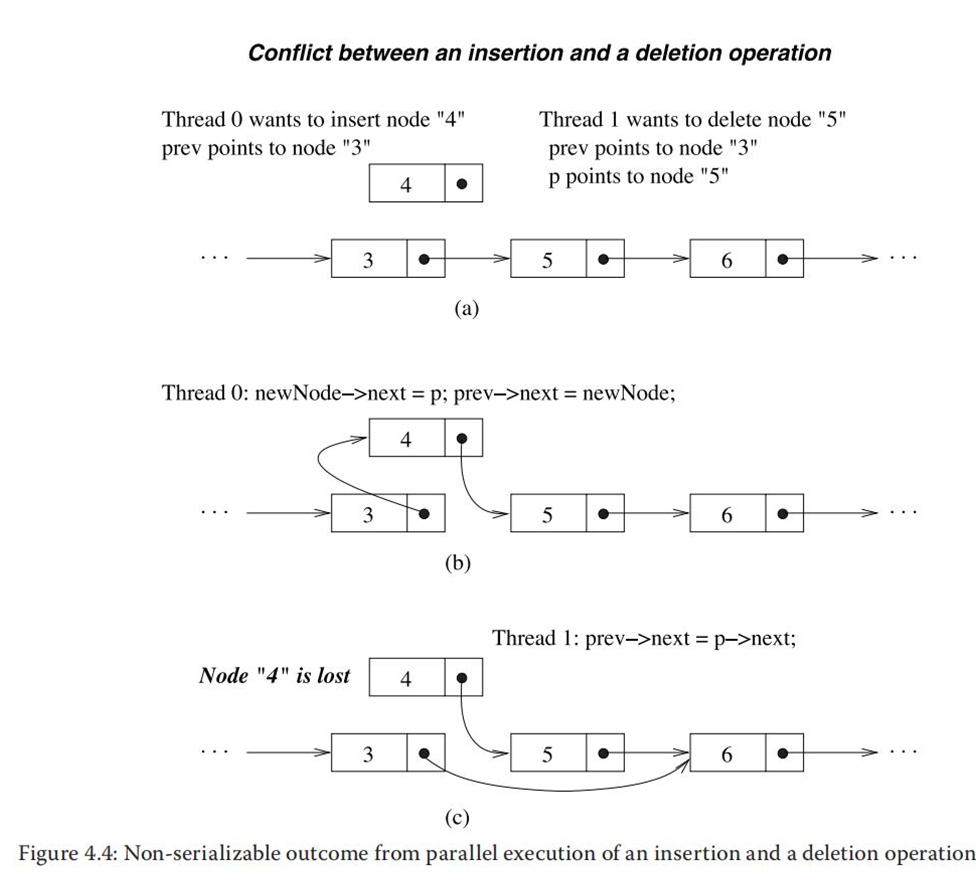
③一个删除和一个搜索操作并行执行产生可串行化结果:
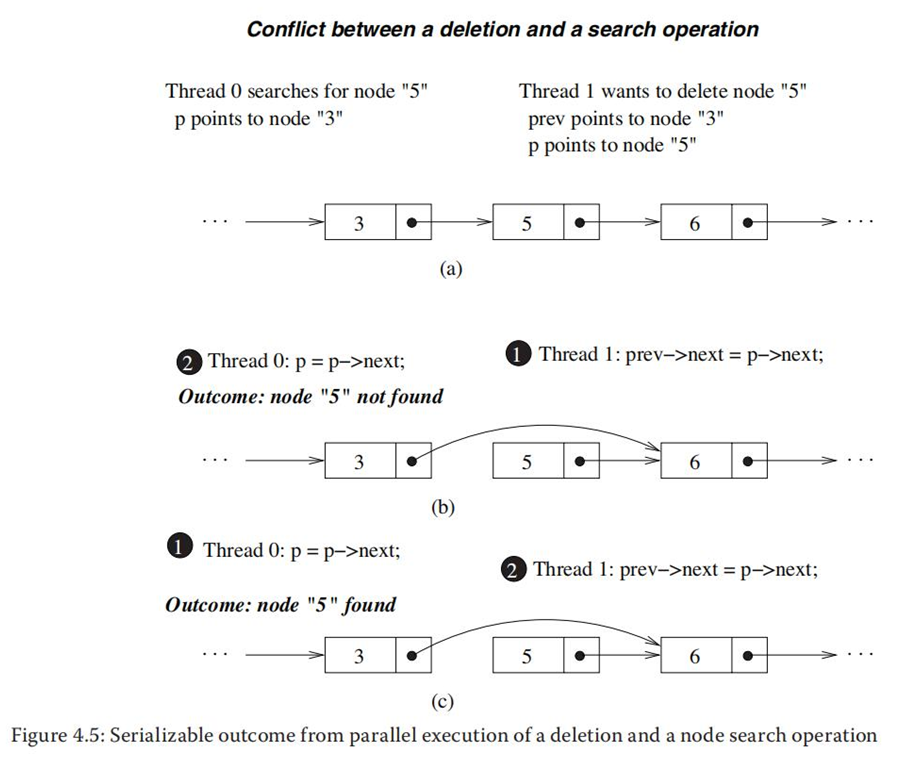
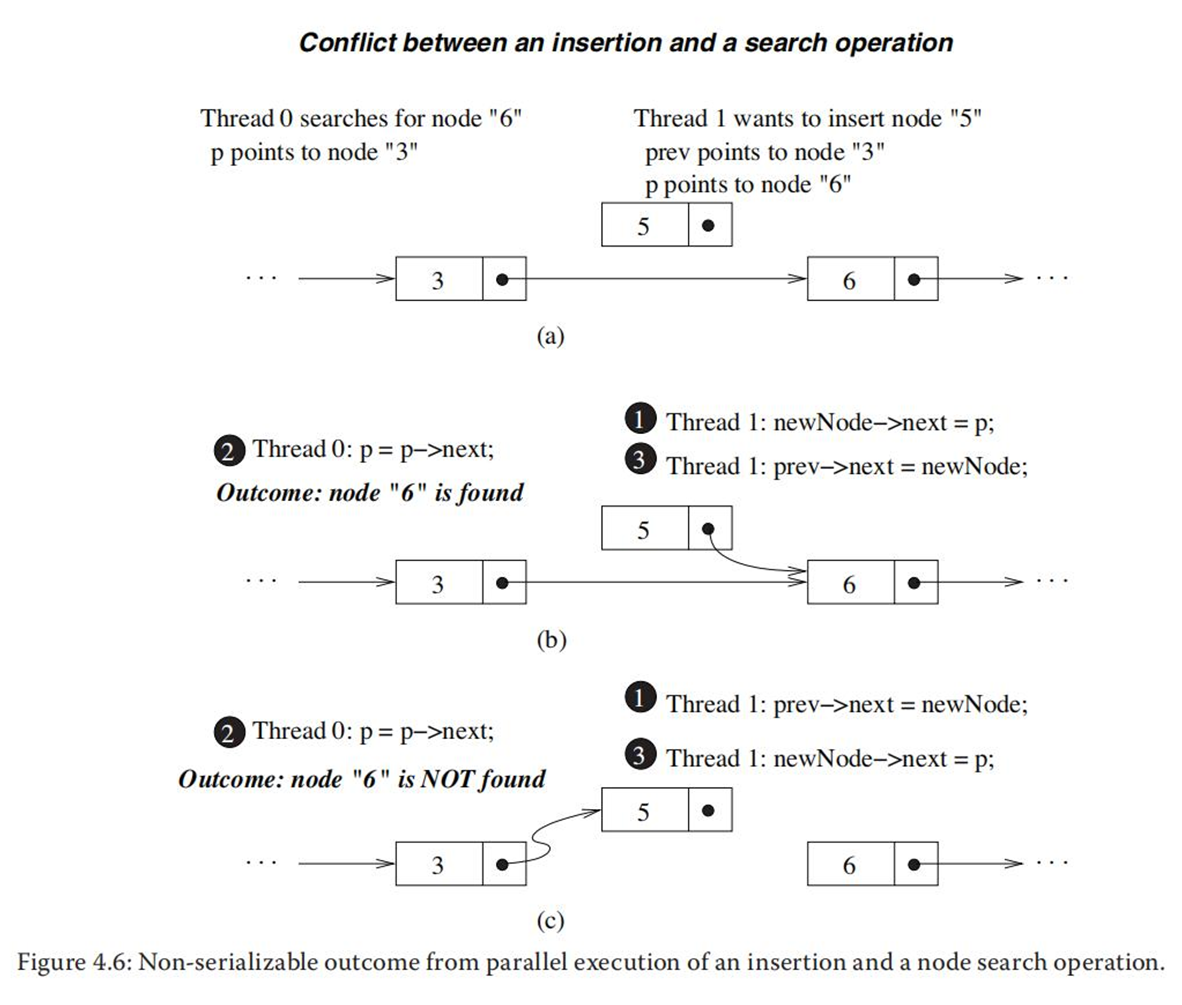
④一个插入和一个搜索操作并行执行产生不可串行化结果
4.3 针对链表的并行化技术
目前有许多面向LDS链表的并行化技术。它们的区别在于并行度和编程复杂度不同。 一般来说,在LDS并行中,并行度越高,其编程复杂度也就越高。程序员需要仔细分析问题以选取合适的并行方案,从而满足其需求和限制。
(1)读操作之间的并行
对于同一链表并行执行的两个操作,若其中一个会修改节点,那么最后可能导致错误结果。如果这两个操作都不修改节点,那么就不会产生错误结果。因此,发掘并行性最简单的办法是只允许只读操作并行执行,而不允许只读操作和读/写操作并行执行。
链表中的基础操作,如插入节点、删除节点和修改节点都会修改链表中的节点。然而,搜索节点并不改变链表。那么就可以让多个搜索节点的操作并行执行,而让修改链表的操作串行执行,如下图所示。如果不经常修改LDS,那么该方法便可获得很高的并行度。否则,可获得的并行度就不会太高。
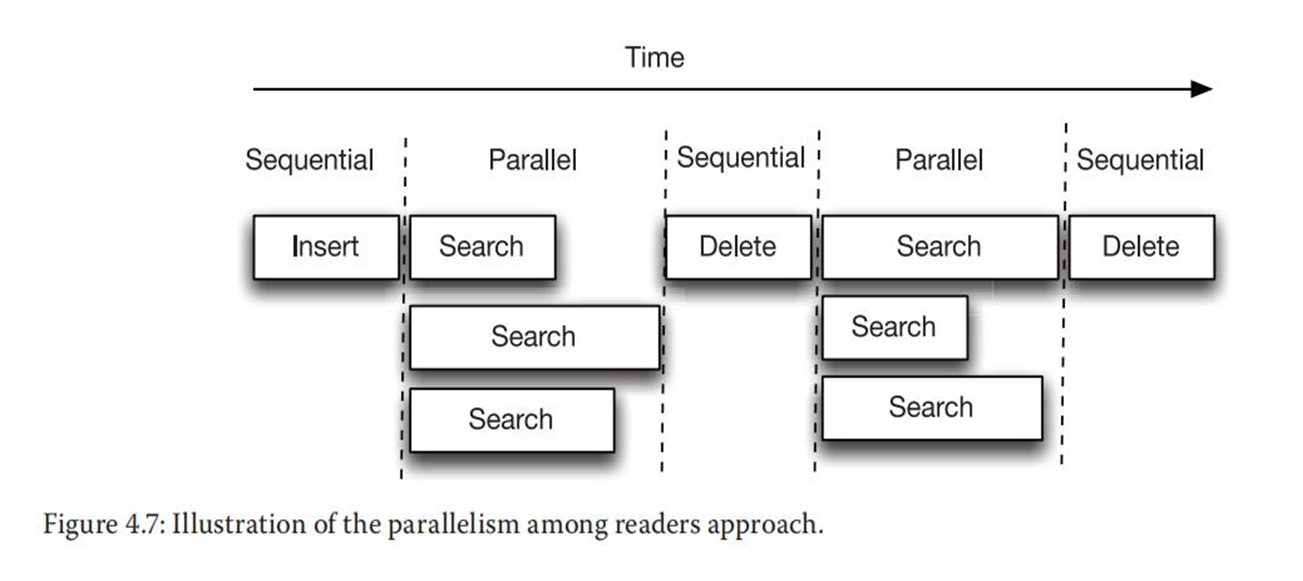
为了实现该方法,需要确保读/写操作和只读操作之间的互斥执行,但在两个只读操作之间不需要互斥。
为了实现这一策略,定义了两种锁:读锁(read lock)以及写锁(write lock)。只读操作执行之前需要获取到读锁,并在执行完后释放该锁。读/写操作执行之前需要获取到写锁,同样地需要在执行完后释放锁。如果读锁已被另一个操作占用,那么可以申请别的读锁,但是写锁只有在当前操作完成之后才能分配给下一个操作。另外,如果写锁已经分配给一个操作,那么读锁和写锁都只有在当前写操作完成并释放写锁之后才能获得。
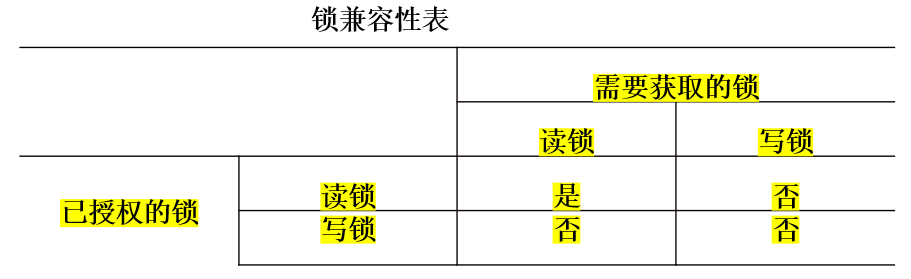
另一种实现读/写锁的方法是使用单个计数器。这种计数器的方法并不需要使用传统的锁,只需要处理器支持加和减的原子操作,比如读取并相加。假设提前知道线程数n,获取读锁时将计数器加1,释放锁时将计数器减1。请求写锁操作时将计数器减n,相应地,释放写锁后将计数器加n。如果计数器之前的值为负,说明当前有写操作正在进行,那么读锁的申请就会失败。如果计数器的值不为0,说明当前有写操作(值为负)或多个读操作(值为正)正在进行,对于写锁的申请就会失败。
为了实现这种方案,每一个操作都可以被封装到封装函数里面,通过调用该函数并根据操作的类型来申请读或写锁,并在操作完成之后释放相应锁。如下面的代码所示,这些封装函数会为插入和删除操作获取写锁,并为搜索操作获取读锁。将锁变量命名为global,以表示LDS的所有操作都依赖该全局变量。
void Insert(plntList pList, int key)
{
setLock(global, WRITE);
Origlnsert(pList, key);
unsetLock(global);
}
void Delete(plntList pList, int key)
{
setLock (global, WRITE);
OrigDelete (pList, key);
unsetLock (global);
}
int Search (plntList pList, int key)
{
setLock(global, READ);
int result = OrigSearch (pList, key);
unsetLock (global);
return result;
}
(2)LDS遍历中的并行
如果在读/写操作和其余的操作之间也允许并行的话,则将会得到更高的并行度。在这种情况下,至少有两种方法能够实现并行:
①一种细粒度的方法是将链表中的每个节点都关联一个锁变量,这样对于每个节点的操作可以用锁分别保护起来。
②另一个更简单的方法是使用一个全局锁来保护整个LDS。
细粒度锁的方法增加了管理锁的复杂度,如需要避免或处理死锁和活锁。使用全局锁的方法就避免了死锁和活锁的情况,由于只有一个全局锁,因此在锁获取过程中没有环形依赖。
在读/写操作之间实现并行的关键在于要将操作分解为对链表只读和对链表更新的操作。逻辑上,链表的插入或删除操作都包含了遍历过程以便找到删除相应的位置来进行操作。一旦定位到相应的位置,就执行修改。由于遍历过程只读链表,因此可以将插入多个遍历操作并行执行。只有当操作需要修改链表的时候,才会申请锁以便执行修改链表操作。
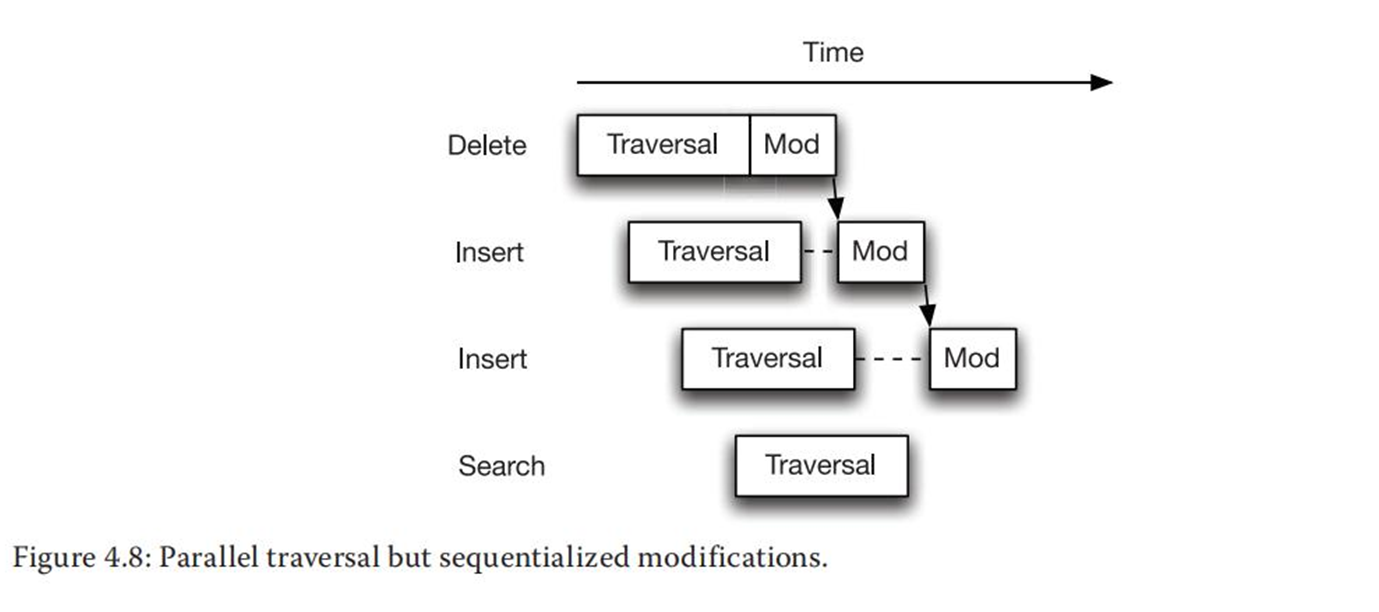
(3)细粒度锁方法
尽管全局锁的方式允许多个操作并行执行,但是该方法仍然存在限制,如一次只允许一个线程修改链表。即使在不同的线程修改链表不同部分的时候,这些线程也必须在临界区内串行执行修改。
对链表中不同部分进行修改的操作能并行吗?为了实现这一目标需要更细粒度的锁。可以将每个节点都分别与一个锁绑定,而不是使用一个全局锁。这里的基本原理是,当一个操作需要修改一个节点时,它就会锁住该节点,从而别的操作不能修改或读取该节点,但是其余修改或读取其他节点的操作就可以无冲突地并行执行。
现在的问题是如何确定每个操作需要锁住的节点。为了解答这一问题,首先需要区分操作中会被修改的节点,以及那些只读但一定要保持有效以便操作能正确完成的节点。处理该问题的思想是:将要被修改的节点需要获取写锁,被读取并需要保持有效性的节点则需要获取读锁。需要注意,过度地(例如使用写锁)对这两种节点使用锁也是不必要的,因为这会使得并发度降低。然而,过于宽松(例如使用读锁)地使用锁又会影响结果的正确性。
在实现细粒度锁方法时,需要注意如果没有以正确的顺序来获取锁,那么可能会出现死锁的情况。在展示的实现中,获取锁的顺序总是从最左边的节点开始。如果插入节点的操作从最左边的节点开始获取锁,但是删除节点的操作从最右边的节点开始获取锁,那么插入节点和删除节点获取锁的方式就会产生环形依赖进而造成死锁。另一种方式是可以通过以节点地址的升序或降序的方式获取锁,以确保所有线程以统一顺序来获取锁。这种方法在数据结构本身没有顺序信息的时候会很有用,如在图结构中。
将细粒度锁和全局锁相比较,对于单链表而言,二者的编程复杂度完全不同。由于链表数据结构的规则性,可以很轻松地将以下三个步骤区分开:
①遍历
②锁住将被修改或需要依赖其有效性的节点
③修改节点
4.4 事务内存
事务内存(Transactional Memory, TM)可以在某种程度上简化LDS并行编程。使用TM最简单的方法就是将每一个LDS操作封装在一个事务中。比如可以这样写:atomic(Insert(---))或者atomic(Delete(---)),这样就可以自动地确保每一个操作与其余操作隔离地执行。如果在插入节点的过程中检测到冲突,那么插入节点事务就会终止并返回失败。同样地,可以将搜索节点的操作封装起来,当任何被遍历或搜索的节点被修改时事务操作可以在提交之前终止。这在很大程度上简化了LDS编程。
但事务内存仍有几点不足。随着LDS结构大小的增加,每一个操作都需要更长的时间才能完成,且大部分时间都在遍历LDS。更长的操作时间会增加两个事务发生冲突的可能性,导致操作回滚且至少有一个事务需要重新执行,这样就降低了性能。即使两个操作修改LDS中不同节点的时候,回滚也是可能发生的。在TM中,当检测到冲突时就会触发回滚,当一个事务的写操作集和另一个事务的读/写操作集重叠时就会检测到冲突。这种情形也叫假冲突(false conflict),因为如果忽略该冲突,并允许这两个非重叠的操作同时执行,那么它们实际会产生可串行化的结果。
总的来说,不管是使用细粒度锁还是TM方法来实现对LDS的并行编程,程序员都需要仔细考虑并发性以及粒度的问题。与使用锁编程类似,事务粒度越细,就会有越多的竞争,同时编程也更复杂。然而,一旦确定了锁的粒度,使用TM则不需要担心维护锁及其数据结构和使用锁的风险(比如死锁),因而TM可以简化使用细粒度锁的编程。对于粗粒度事务,由于事务被终止的可能性很大,仍然可能需要用到锁,因此程序员需要认真地考虑哪种情况需要使用锁、哪种情况需要使用事务,以及使用事务与使用锁的代码之间如何交互。
课堂习题:
习题1
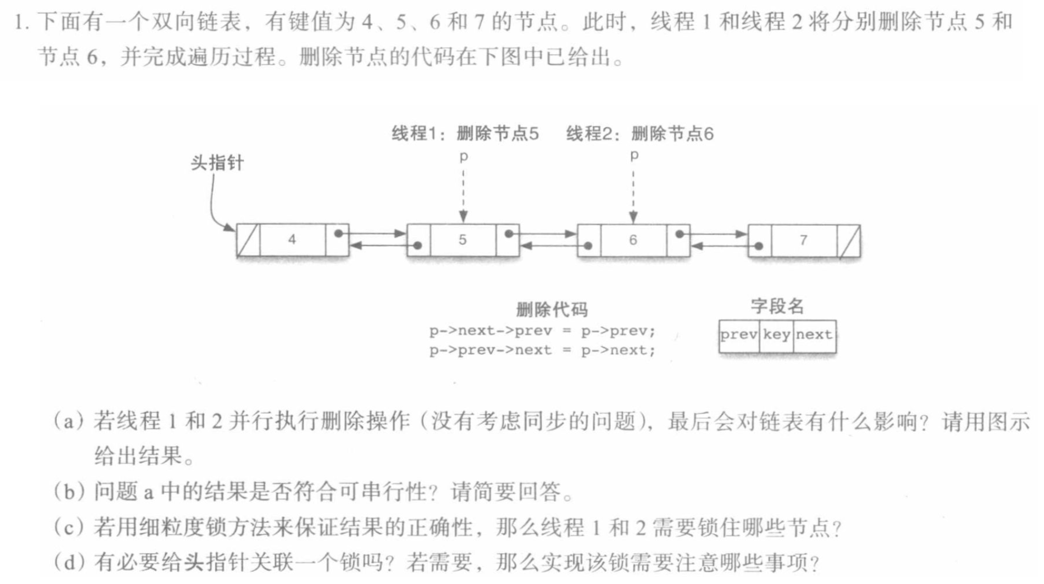
(a)
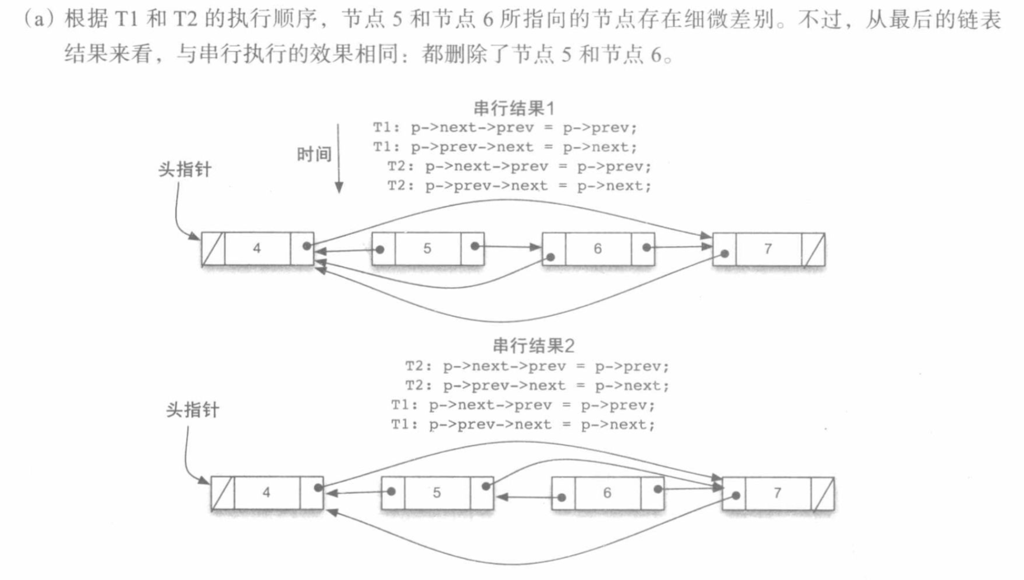
(b)

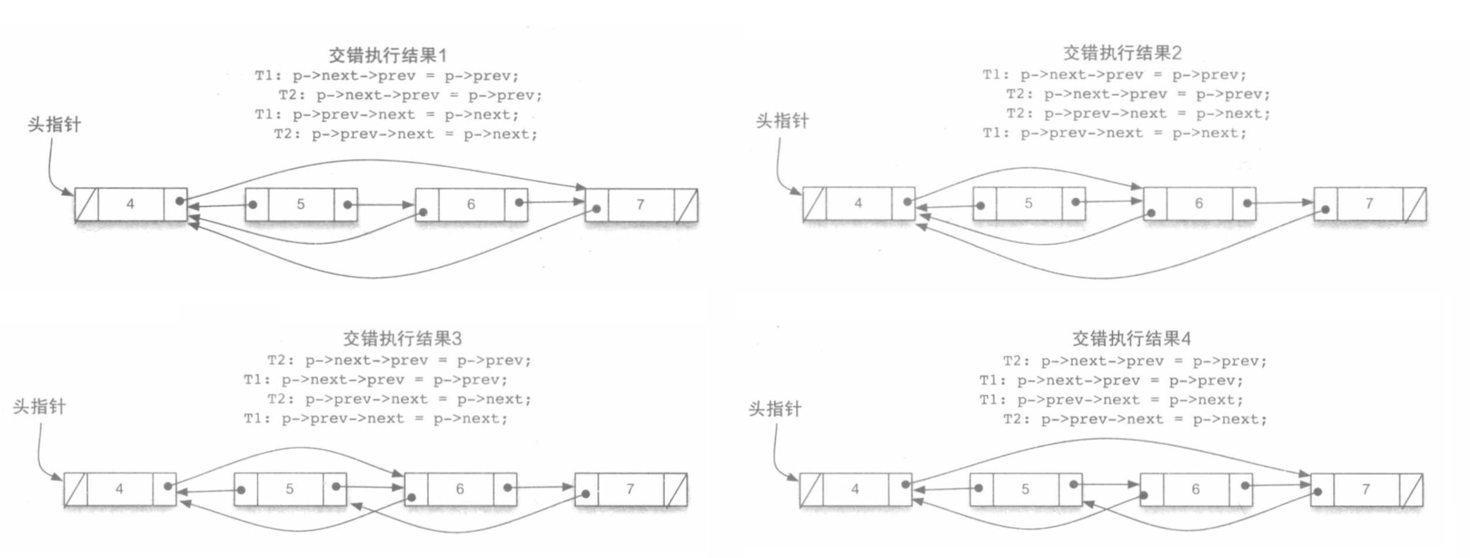
(c)
处理该问题的思想是:将要被修改的节点需要获取写锁,被读取并需要保持有效性的节点则需要获取读锁。

(d)

课后习题:
重点题目:1,2,3,4
习题1
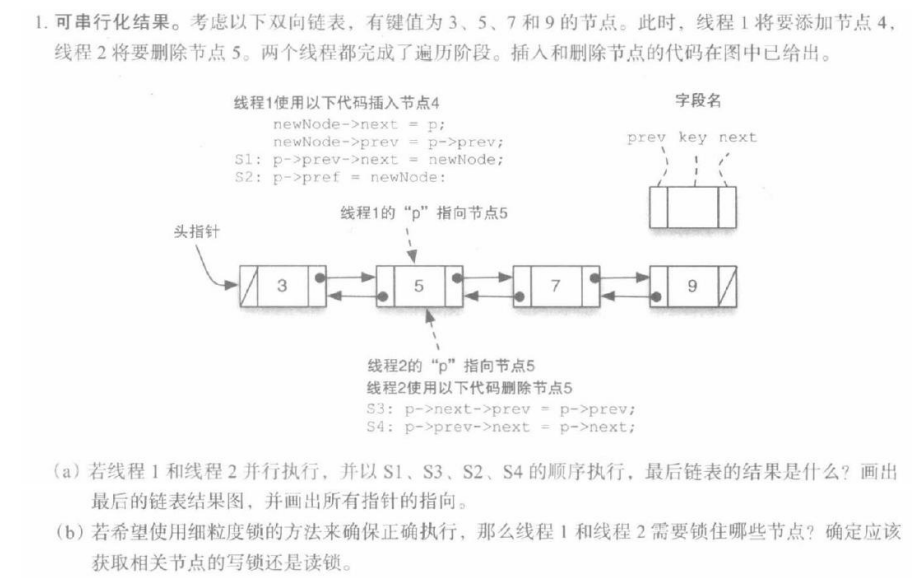
(a)
(b)
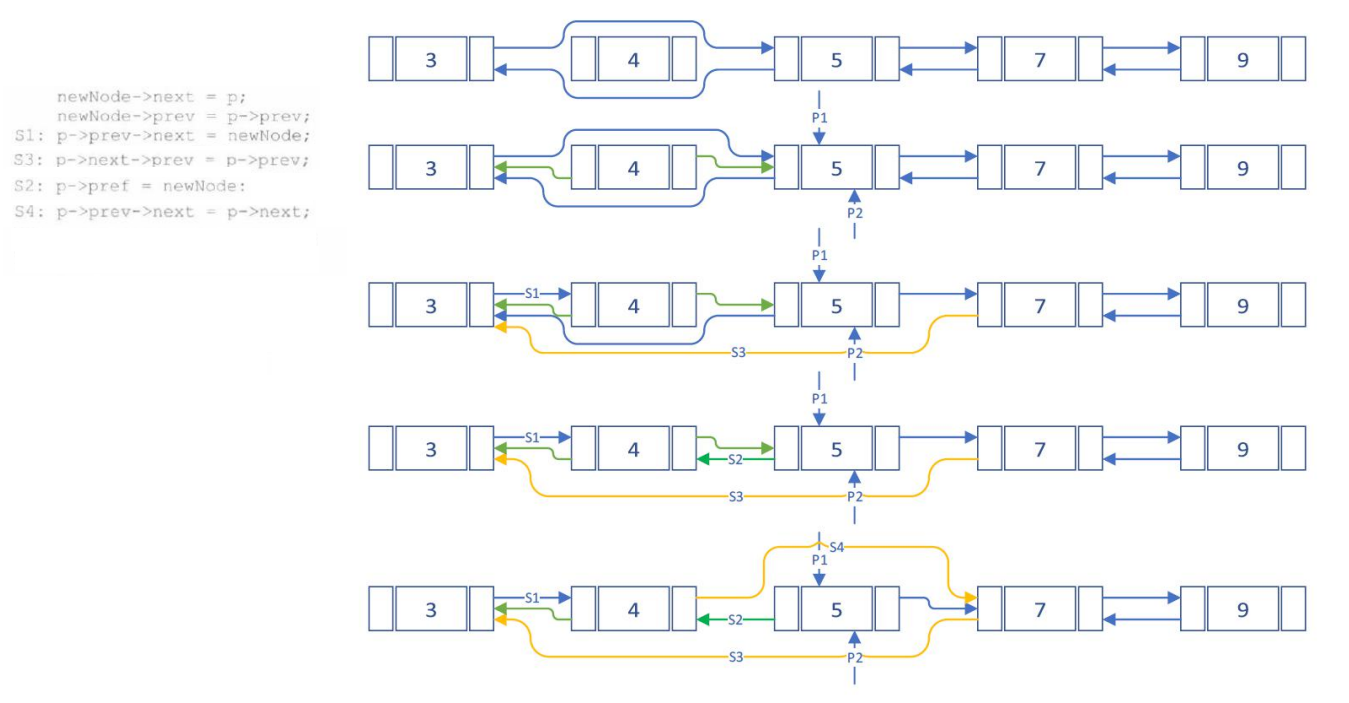
处理该问题的思想是:将要被修改的节点需要获取写锁,被读取并需要保持有效性的节点则需要获取读锁。
线程1需要使用写锁的节点为:3、4、5;
线程 2 需要使用写锁的节点为:3、7,读锁的节点为 5
习题2

两个删除操作,此时假设线程1和线程2为删除操作,则它们执行的先后顺序并不影响串行化结果,应该考虑被删除节点的位置。
1、如果要被删除的两个节点不相邻,则可串行化
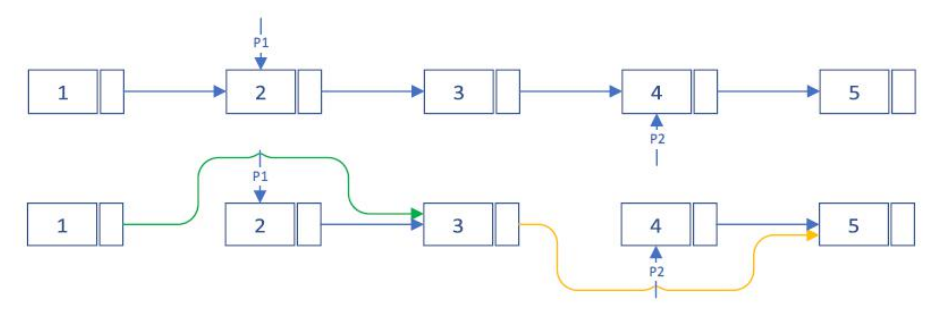
2、如果要被删除的两个节点相邻,则不可串行化
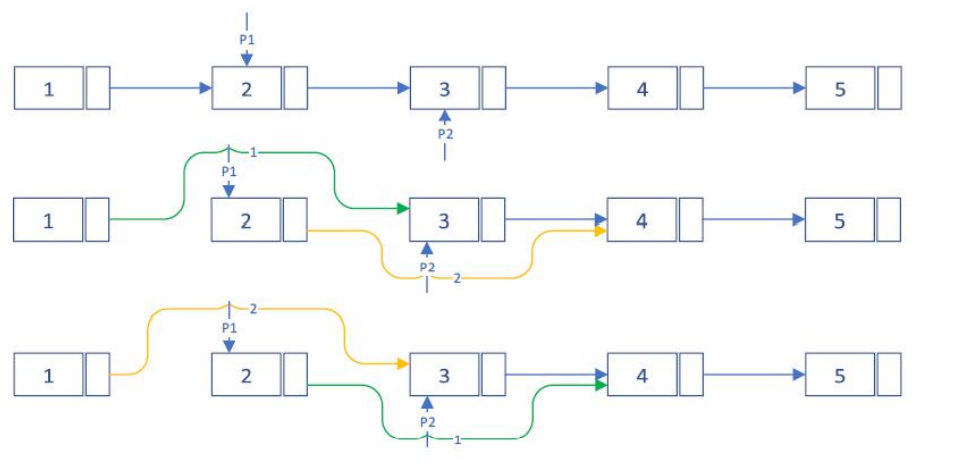
习题3

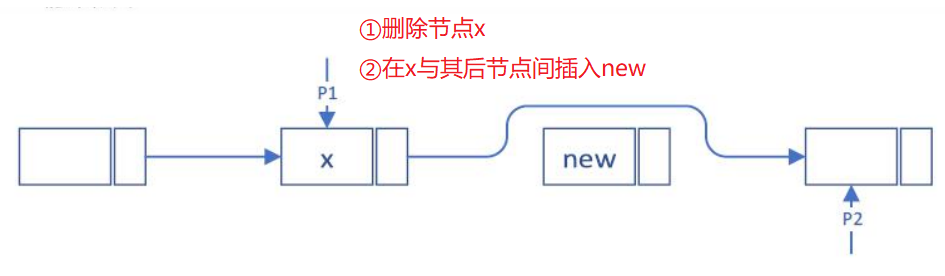
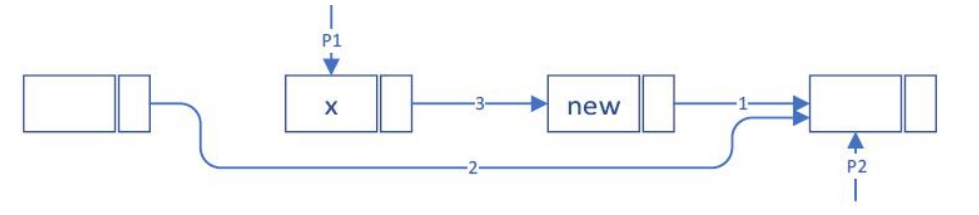
P1:执行删除节点 x 的操作(标记 x 节点为 p1,x 之前节点为 prev1)
S1: prev1->next=p1->next
P2:执行在 x 及其后节点之间插入 new,(标记 x 节点为 prev2,x)
S2: new->next=p2
S3: prev2->next=new
分别按照 S1,S2,S3; S2,S1,S3; S2,S3,S1 的顺序执行,结果均相同,如下图:
习题4

(a)
//插入节点(插入p节点之前)
S1: newNode->next=p;
S2: newNode->prev=p->prev;
S3: p->prev->next=newNode;
S4: p->prev=newNode;
//删除节点(删除 p)
S5: p->prev->next=p->next;
S6: p->next->prev=p->prev;
下面两个操作参考上述代码:
(b)
处理该问题的思想是:将要被修改的节点需要获取写锁,被读取并需要保持有效性的节点则需要获取读锁。
插入节点需要 p->prev, p 写锁。
(c)
删除节点需要 p->prev,p, p->next 的写锁
习题5

答:在图或树中按照节点地址的升序(或降序)获取锁时,存在以下问题:
(1) 某些锁在后面才能用到,但是因为其地址较小(或较大)的原因,需要先获取,增加了线程(或进程)持有锁的时间,改变了锁使用的顺序,这些都需要通过编程来处理,增加了编程的难度。
(2) 在多个线程通过锁的方式协作处理事务时,改变锁的获取顺序,可能使得线程之间的协作无法进行。
习题6

(1)
单向链表中,插入节点时,需要 prev 的写锁,p 的读锁;删除节点时,需要 prev, p 的写锁,p->next 的读锁。
插入时,按照节点被访问概率相同的假设,如果均为写锁,则所能达到的最大并发数量为 n/2;若 1/2 锁为写锁,另 1/2 锁为读锁,则被读锁锁住节点可继续被其他 线程读,所能达到的最大并发数量为 n/2+n/4+n/8+…。读锁变为写锁,损失并发数 为 n/4+n/8+…
删除时,按照节点被访问概率相同的假设,如果均为写锁,则所能达到的最大并发数量为 n/3;若 2/3 锁为写锁,另 1/3 锁为读锁,则被读锁锁住节点可继续被其他 线程读,所能达到的最大并发数量为 n/3+n/9+n/27+…。读锁变为写锁,损失并发数 为 n/9+n/27+…
插入与删除操作相等,则并发数损失为 1/2(n/4+n/8+…+n/9+n/27+...)
(2)
双向链表均需要写锁,不存在因读锁变写锁使得并发数减少的问题。
习题7

删除操作中如果获取了节点的锁而没有及时删除相应节点,如果此时有搜索的线程, 将会导致搜索结果出错。
解决方案①搜索过程使用蜘蛛锁;②使用事务内存
习题8

方案(1)搜索链表时,通过蜘蛛锁给当前的节点加锁。
方案(2)给节点添加时间戳的域,用以判断节点是否已经变化。
方案(3)使用事务内存。
方案(1)会影响链表操作的并发数;方案(2)有额外的空间开销和判断开销;方案 (3)事务锁存在冲突问题。

 记一下插入、删除操作代码
记一下插入、删除操作代码

