并行多核体系结构基础——第三章知识点和课后习题

本章的目的主要是讨论创建共享存储并行程序所需的步骤，重点在于通过分析代码来识别出可以并行的任务、确定变量的范围、协调并行任务，以及向编译器展现并行性。在最后，将学习基本的共享存储并行编程技术。

知识点：

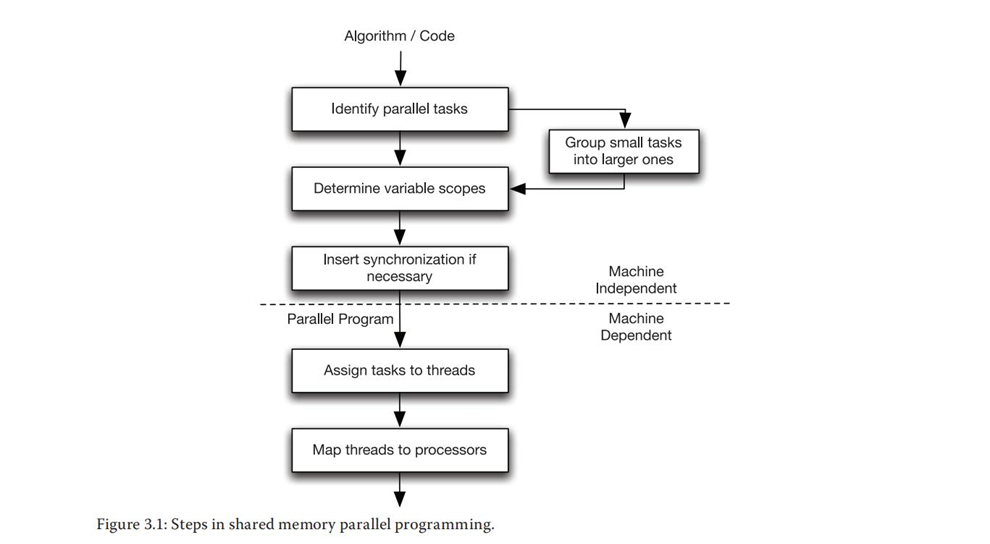
3.1并行编程的步骤

共享存储并行编程：

3.2依赖分析 ⭐⭐⭐

目标是 发现是否有可以并行执行的代码段 。

依赖分析需要处理的第一个问题是 如何确定代码分析的粒度。

举个栗子：

S1: x = 2;
S2: y = x;
S3: y = x + z;
S4: z = 6;

S1→^TS2，因为x在S1中写入并在S2中读取。

S1→^TS3，因为x在S1中写入并在S3中读取。

S3→^AS4，因为z在S3中读取并在S4中写入。

S2→^OS3，因为y在S2中写入并在S3中也写入。

反依赖和输岀依赖也被称为假依赖，因为后续指令并不依赖于先前指令产生的任何值。该依赖关系只是因为它们涉及相同的变量或存储位置。因此，通过重命名变量实际上可以消除假依赖。

真依赖一般难以消除，因此它们是并行化的真正障碍。并行程序中消除假依赖的典型方法被称为私有化。

（1）循环级依赖分析

括号“[]”内表示循环迭代空间。例如，迭代空间 [i,j]表示在外层循环上迭代i次并在内层循环上迭代j次的双重嵌套循环。S[i,j]表示在特定迭代[i,j]中执行的语句S。如果将整个循环体作为一个语句组，S[i,j]表示迭代[i,j]中的整个循环体。

① 循环传递依赖可以定义为一次迭代中的语句与另一次迭代中的语句之间存在的依赖关系。

② 循环独立依赖为循环迭代内部语句之间存在的依赖关系。

举个栗子：

for (i=l; i<n; i++) 
{
	S1: a[i] = a[i-1] + 1;
	S2: b[i] = a[i];
}

for (i=l; i<n; i++)
	for (j=l; j< n; j++)
		S3: a[i][j] = a[i][j-1] + 1；
            
for (i=l; i<n; i++)
	for (j=l; j< n; j++)
		S4: a [i][ j] = a [i-1][ j] + 1；

第一个循环（S1）中的第一条语句，读取a[i-1]并对a[i]写入,这意味着写入a[i]的值会在下一次迭代中被读取（第i+1次迭代）。因此，有循环传递依赖S1[i]→^TS1[i+1]。 例如，在迭代i=4时，语句S1写入a[4]并读取a[3], a[3]的值是在迭代i=3时写入的。

除此之外，在同一次迭代中写入a[i]的值被S2语句读取，因此有S1[i]→^T S2[i]循环独立依赖 。

在第二层循环中，a[i] [j]中写入的值会在接下来的第j+1次迭代中读取，因此有依赖S3[i, j]→^TS3[i,j+1],其中对for j循环而言是循环传递依赖，而对for i循环而言是循环独立依赖。

在第三层循环中，a[i] [j]中写入的值会在接下来的第i+1次迭代中读取，因此这里有S4[i, j]→^TS4[i+1, j]依赖，其中对for i循环而言是循环传递依赖，而对for j循环而言是循环独立依赖。

总体来说，依赖关系如下：

S1[i]→^TS1[i+ 1]

S1[i]→^TS2[i]

S3[i,j]→^TS3[i,j+1]

S4[i,j]→^TS4[i+1,j]

（2）迭代空间遍历图ITG和循环传递依赖图LDG

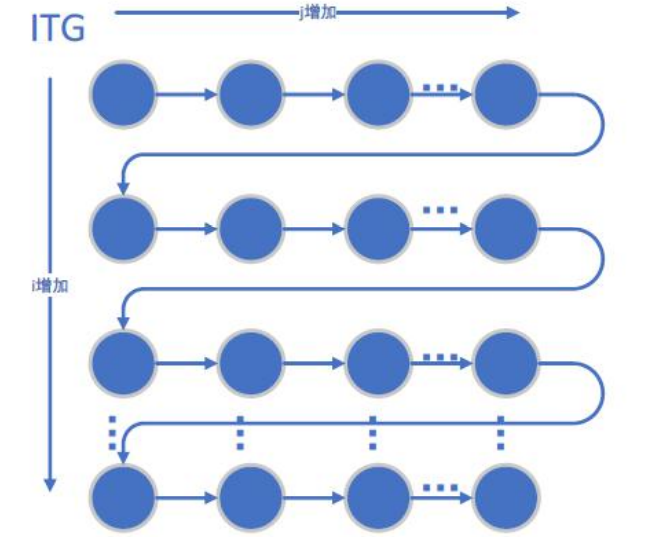
①ITG：以图形方式展示了迭代空间中的遍历顺序。ITG不能显示依赖性; 它只显示循环迭代的访问顺序。

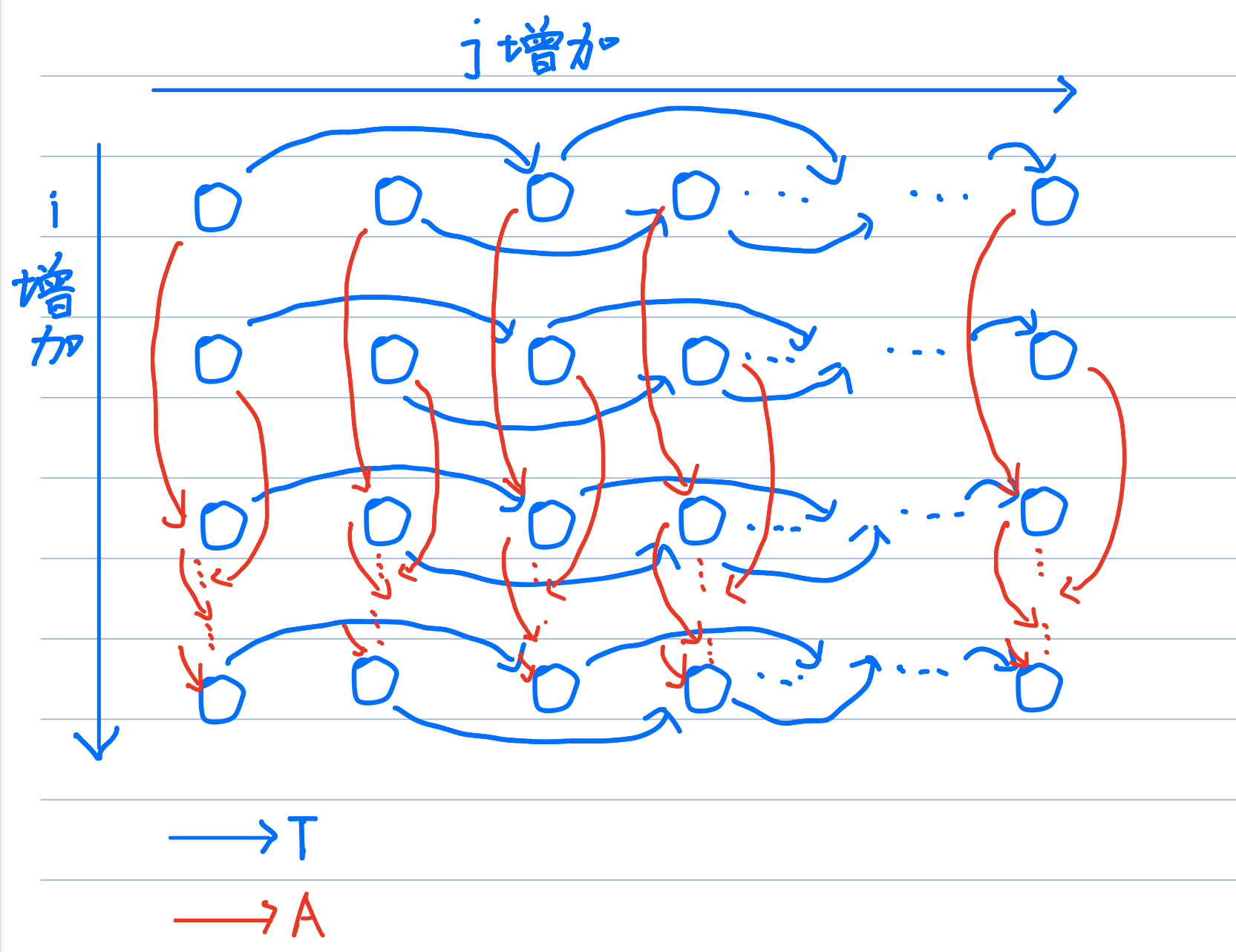
②LDG：以图形方式展示了真/反/输岀依赖，其中一个节点就是迭代空间中的一个点，而有向边显示依赖的方向。换句话说，LDG将最内层循环体中的所有语句视为一个语句组。由于一个节点代表一次迭代中的所有语句，所以LDG不显示循环独立依赖。本质上来说，LDG可以通过绘制每个迭代的依赖关系获得。

快速记忆：

①ITG：访问顺序，看for循环

②LDG： just传递，no独立

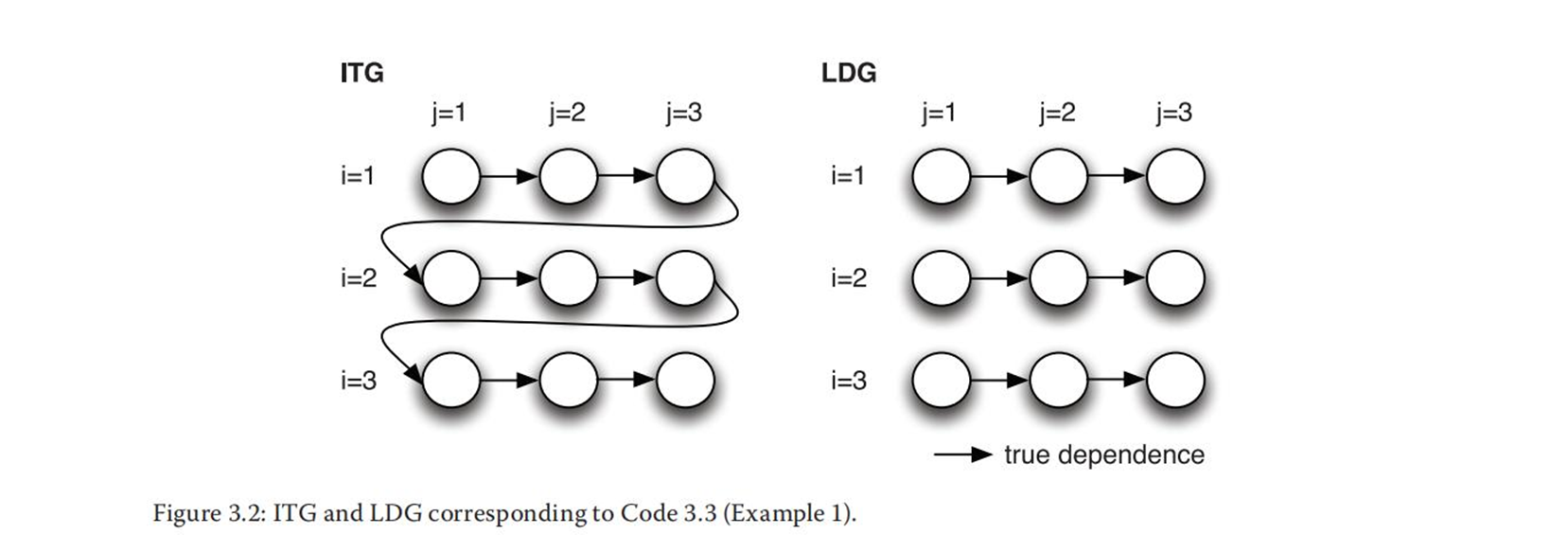
举个栗子：

for (i=1; i<4; i++)
	for (j = 1; j<4; j++)
		S3: a[i][j] = a[i][j-1] + 1;

S3[i,j]→^TS3[i,j+1] //for a

i是循环独立，j是循环传递

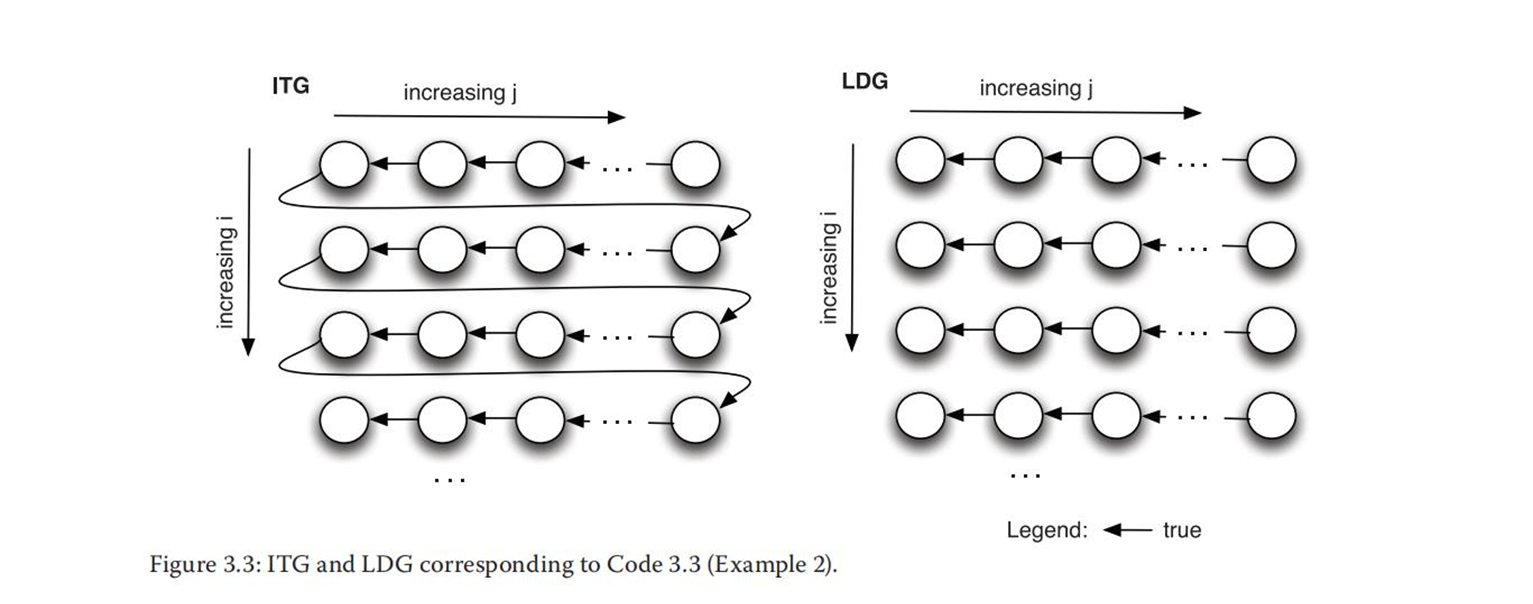
for (i=0; i<n; i++) 
{
	for (j=n-2; j>=0; j--) 
    {
		S2: a[i][j] = b[i][j] + c[i][j];
		S3: b[i] [j] = a[i] [j+1] * d[i] [j];
	}
}

S2[i,j]→^TS3[i,j-1] //for a

S2[i,j]→^AS3[i,j] //for b

i是循环独立，j是循环传递

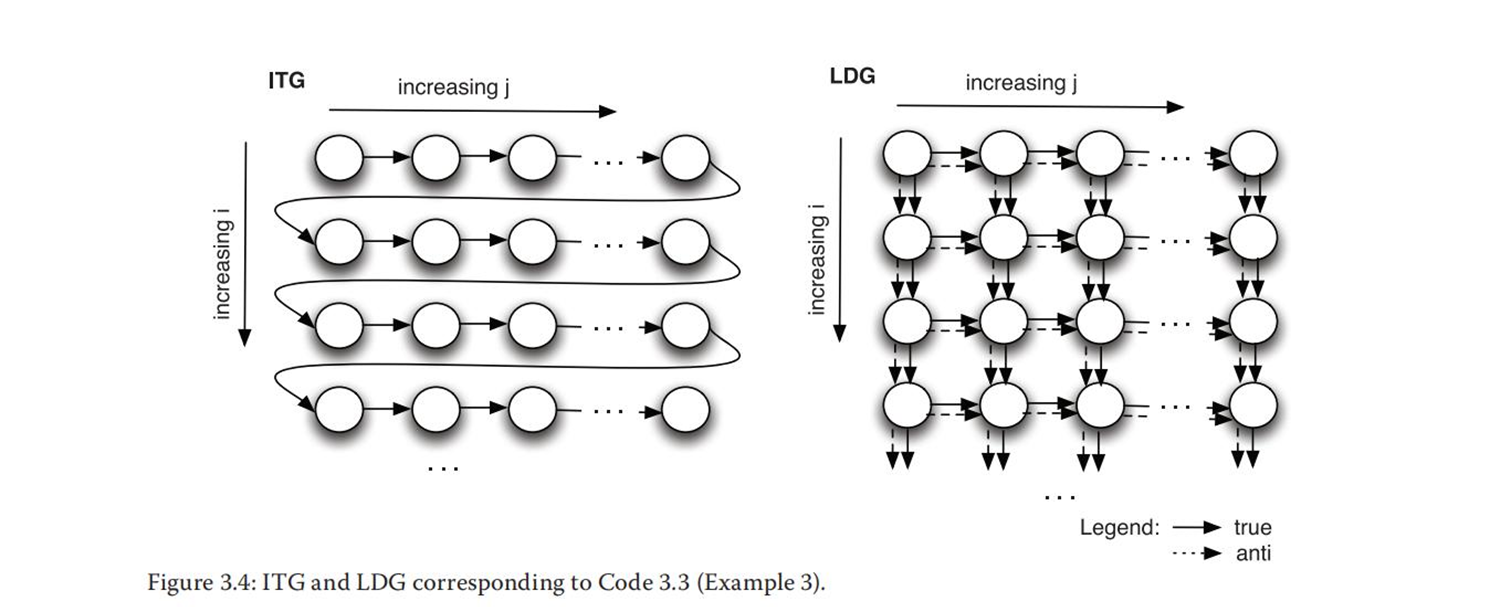
for (i=1; i<=n; i++)
	for (j=l; j<=n; j++)
		S1: a[i][j] = a[i][j-1] + a[i][j+1] + a[i-1][j] + a[i+1][j];

S1[i,j]→^TS1[i,j+1]

S1[i,j]→^TS1[i+1,j]

此处，反依赖的理解：

语句a[i] [j+1]部分再迭代[i,j]中读取的值还未被写入并将在迭代[i,j+1]中被写入。

同理，语句a[i+1] [j]部分在迭代[i,j]中读取的值将在迭代[i+1,j]中被写入。

S1[i,j]→^AS1[i,j+1]

S1[i,j]→^AS1[i+1,j]

i,j都是循环传递

3.3识别循环结构中的并行任务

（1）循环迭代间的并行和DOALL并行

分析哪些循环迭代可以被并行执行是识别并行的最有效的方法之一。为了做到这一点，首先要分析循环传递依赖。第一个原则是必须遵守依赖关系，特别是真依赖。反依赖和输出依赖可以通过私有化移除。暂时假定必须遵守所有的依赖关系。 在LDG中可以通过观察连接代表迭代的两个节点的边直观地看出两个迭代之间的依赖关系。迭代之间的依赖关系也可以被看作连接两个节点的路径（一组边）。只有当两个节点之间没有连接边或路径时，才可以说这两个节点之间没有依赖。彼此之间没有依赖的迭代可以被并行执行。

举个栗子：

for（i=2; i<=n; i++）
	S: a[i] = a[i-2];

S[i]→^AS[i+2]

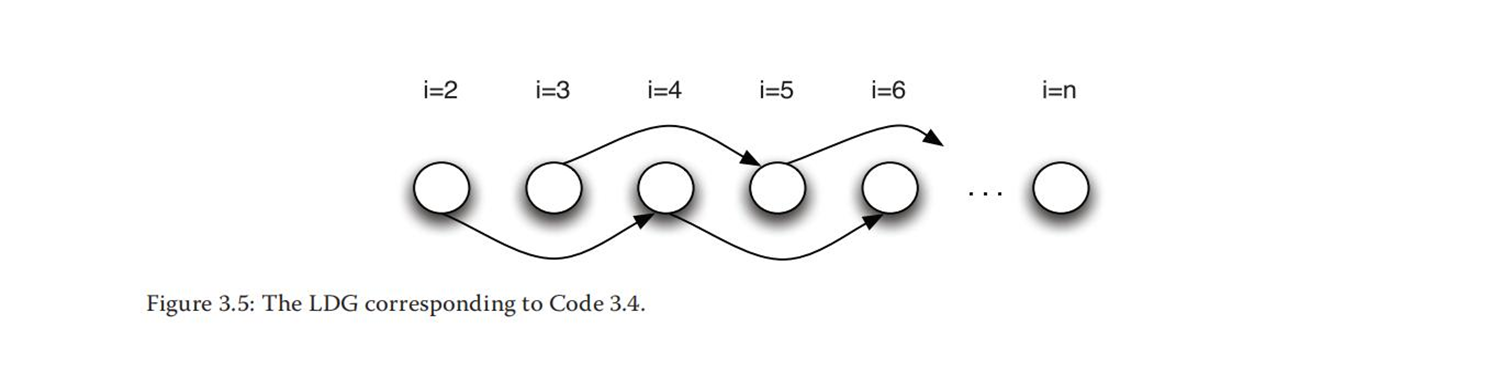
从LDG中可以看到，奇数迭代没有指向偶数迭代的边,偶数迭代也没有指向奇数迭代的边。因此，这里可以提取两个并行任务：一个执行奇数迭代，另一个执行偶数迭代。为了实现这一点，可以将循环分成两个较小的循环。这两个循环现在可以相互并行执行，尽管每个循环内仍然需要顺序执行。

此时，将上述代码的原循环拆分得到的新循环：

for(i=2; i<=n; i+=2)
	S: a[i] = a[i-2];
for(i=3; i<=n; i+=2)
	S: a[i] = a[i-2];

还可以惊奇的发现：

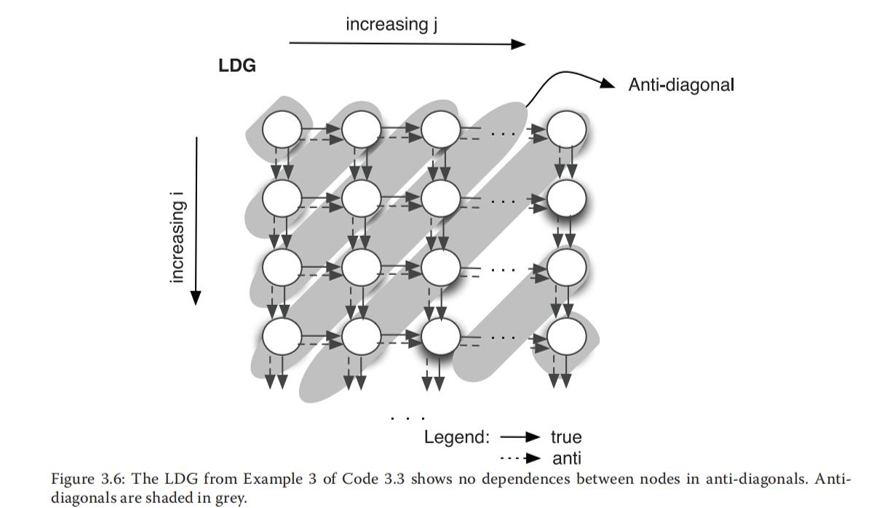
对角线方向也可以没有依赖关系。

不幸的是，为编译器指定这样的并行任务并不容易。例如，OpenMP并行指令只允许为特定的循环指定DOALL并行，但不允许指定循环嵌套中两个循环之间的反对角线并行。解决上述缺陷的一个方法是重构代码，即一个循环遍历反对角线，而另一个内层循环遍历一个反对角线的节点。然后可以为内层循环指定DOALL并行。重构伪代码如下：

计算反对角线的数量
	对每条反对角线
	{
		计算当前反对角线,上点的数量
		对当前反对角线上的每个点
			计算矩阵中的当前点
	}

（2）DOACROSS：循环迭代间的同步并行

DOALL并行很简单，因为它所应用的循环中所有迭代都是可并行任务。通常，DOALL并行循环中并行任务的数量非常大，因此在识别其他类型的并行之前 应该先尝试识别DOALL并行。然而，在一些循环中，由于循环迭代中的循环传递依赖，导致DOALL并行不可行。在这种情况下如何提取并行性？

此时，引入DOACROSS并行。对于即使存在传递依赖的循环，DOACROSS并行也可以提取并行任务。

举个栗子：

for (i=l; i<=N; i++)
	S: a[i] = a[i-1] + b[i] * c[i];

S[i]→^TS[i+1]

i是循环传递

很明显，此时没有DOALL并行性。但b[i]与c[i]相乘的语句没有循环传递依赖，这就带来了并行的机会。

有两种方法可利用这个机会：

①将循环拆分成两个循环

第一个循环只执行没有循环传递依赖的语句部分，而第二个循环只执行有循环传递依赖的语句部分。

for(i=1;i<=N;i++)  //该循环具有DOALL并行
    S1: temp[i] = b[i] * c[i];
for(i=1;i<=N;i++)  //该循环没有
    S2: a[i] = a[i-1] + temp[i];

②在具有部分循环传递依赖的循环中提取并行任务的解决方案是采用DOACROSS 并行性

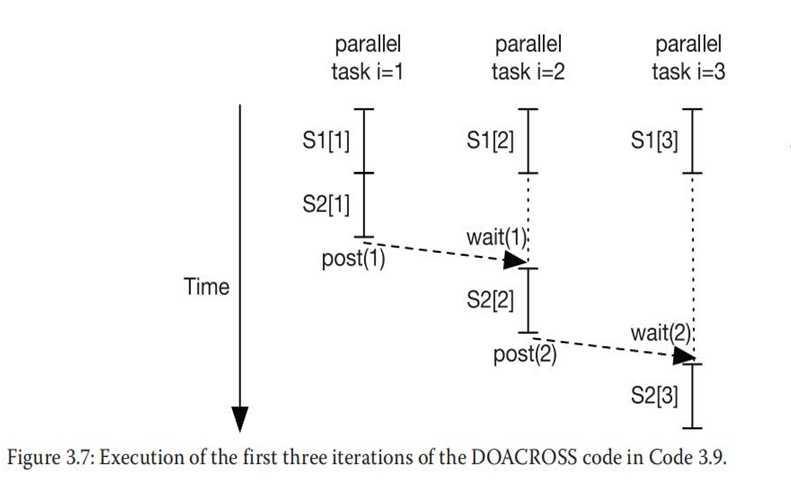
其中每个迭代仍然是并行任务(类似于DOALL)，但插入了同步以确保使用者迭代 (consumer iteration)只读取产生者迭代(producer iteration)产生的数据。

post (0);
for (i=l; i<=N; i++) 
{
	S1: temp = b[i] * c [i];
	wait (i-1);
	S2: a[i] = a[i-1] + temp;
	post (i);
}

（3）循环中语句间的并行

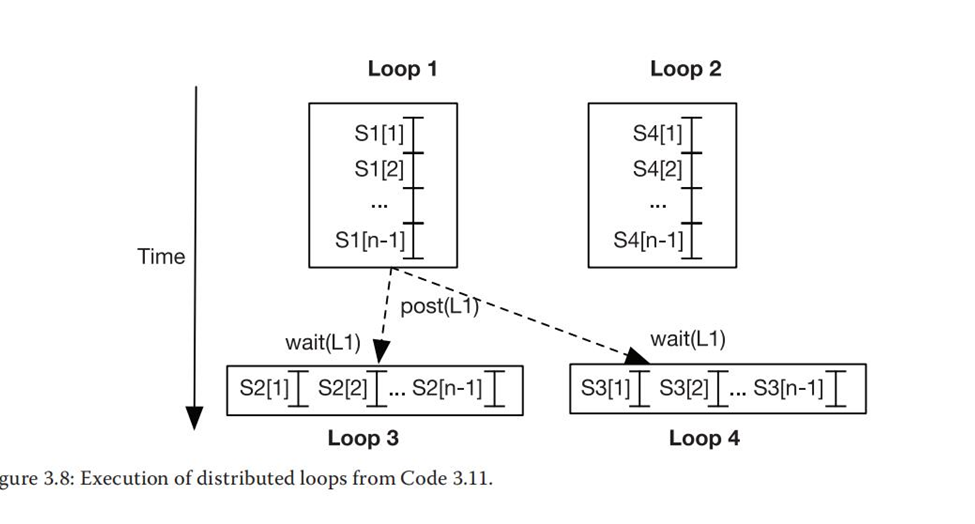
当一个循环具有循环传递依赖时，另一种并行化的方法是将一个循环分发（distribute） 到几个循环中，这些循环执行来自原始循环体的不同语句。

举个栗子：

for (i=0; i<n; i++)
{
	S1: a[i] = b[i+1] * a[i-1];
	S2: b[i] = b[i] * coef;
	S3: c[i] = 0.5 * (c[i] + a[i]);
	S4: d[i] = d[i-1] * d[i];
}

函数并行：每个并行任务在不同数据集上执行不同的计算。

（4）DOPIPE:循环中语句间的流水线并行

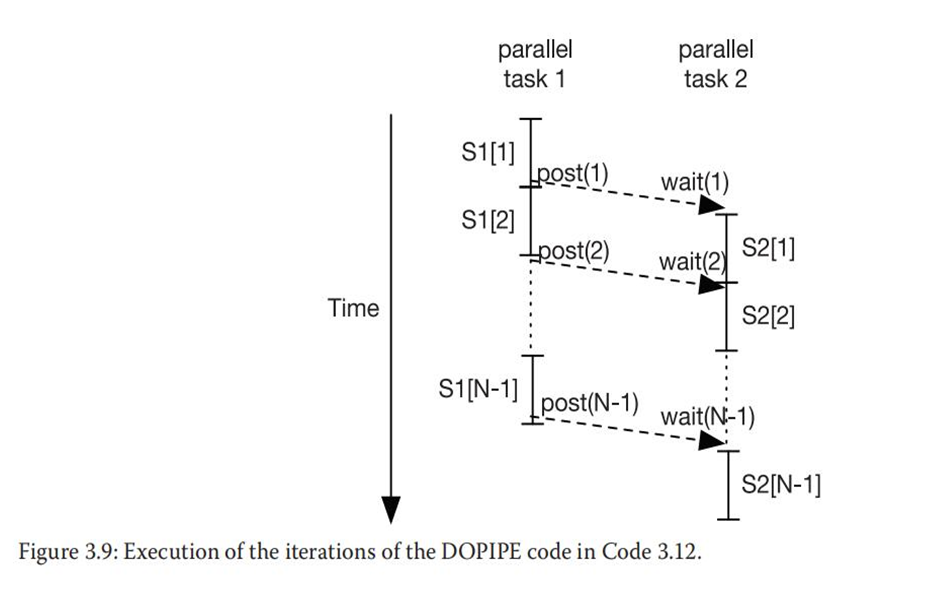
3.4识别其他层面的并行

上述代码是二进制遍历的代码，它以深度优先的搜索方式遍历整个树，并计算和存储了与被搜索的数据相匹配的节点数目。依赖分析揭示了以下依赖:

由于对count的真依赖，有S1→^TS2

由于对count的真依赖，有S1→^TS3

由于对count的真依赖，有S1→^TS4

由于对count的真依赖，有S2→^T3

由于对count的真依赖，有S2→^TS4

由于对count的真依赖，有S3→^TS4

新代码中真依赖数量变少：

由于对count1的真依赖，有S1→^TS2

由于对count2的真依赖，有S1→^TS3

由于对count3的真依赖，有S1→^TS4

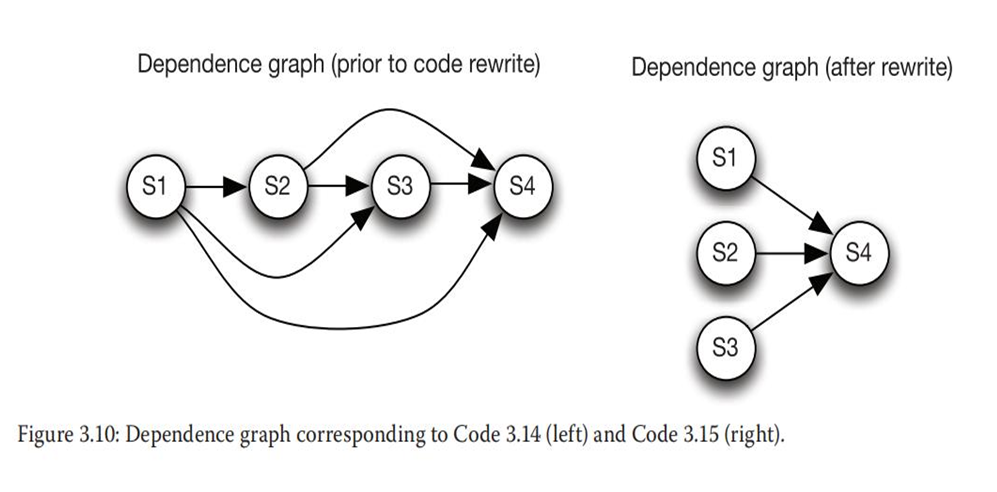
3.5通过算法知识识别并行

分析算法可以带来更多机会以提取并行任务。这是因为代码结构中嵌入了不必要的串行，这是串行编程语言的产物。

举个栗子，考虑一个算法来更新一个水粒子受到相邻的4个水粒子的作用力：

主循环的计算算法是：

While未收敛到一个解do ：
foreach 时间步 do:
	foreach横截面do一次扫描：
		oreach横截面中的点do：	//主循环
			计算与邻居粒子的相互作用力

然后实际的主循环代码引入了人为遍历顺序：

for(i=1; i<=N; i++) 
{
	for(j=1;j<=N; j++) 
    {
		S1: temp = A[i] [j];
		S2: A[i][j] = 0.2 * (A[i][j]+A[i][j-l]+A[i-l][j]  +A[i][j+l]+A[i+l][j])；
		S3: diff += abs(A[i][j]-temp);
	}     
}

分析代码表明唯一的并行机会在反对角线上，因此必须重构代码来利用这个并行机会。 然而，计算的基本算法事实上并没有指定任何特定的顺序，从而确定必须优先更新的横截面的元素。该算法仅指定在一次扫描中，横截面中的每个点必须通过考虑与其邻居的交互来更新一次。

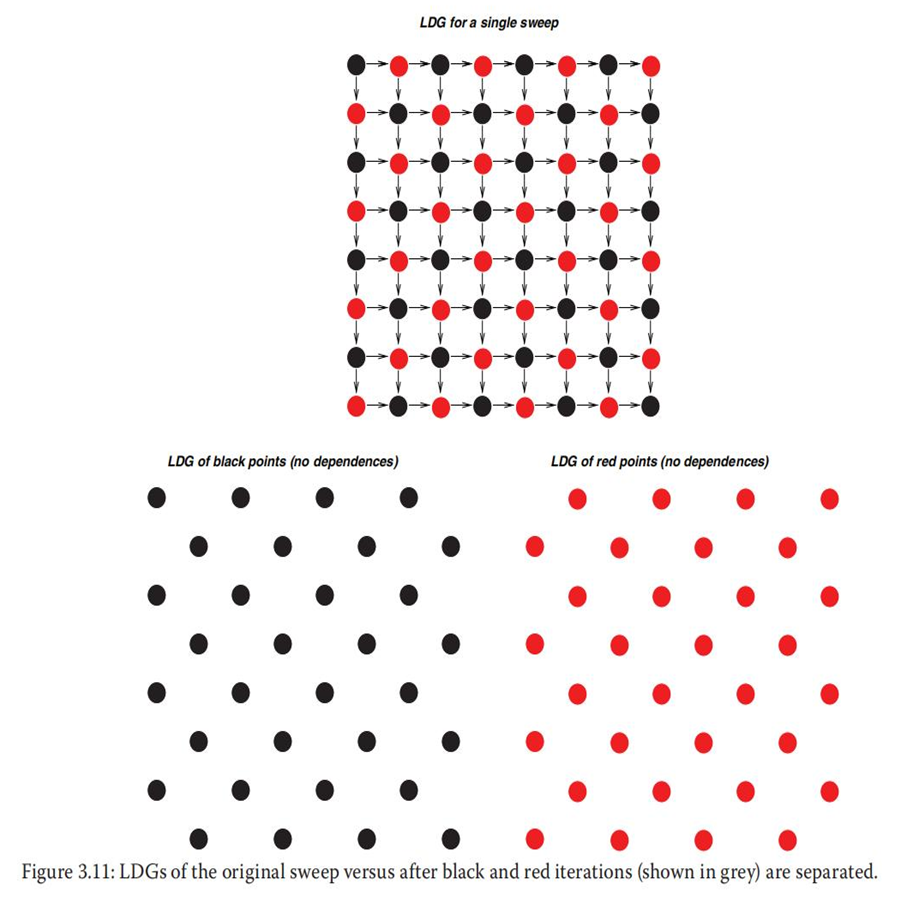
洋流仿真的红黑分区：

//带有DOALL并行的外部和内部循环的黑色扫描
for (i=1; i<=N; i++)
{
	offset = (i+1) % 2;
    for (j=1+offset; j<=N; j+=2)
    {
     	S1: temp = A[i][j];
     	S2: A[i][j] = 0.2 * (A[i][j]+A[i][j-1]+A[i-1][j]+A[i][j+1]+A[i+1][j]);
     	S3: diff += abs(A[i][j] - temp);}
//带有DOALL并行的外部和内部循环的红色扫描
for (i=1; i<=N; i++) 
{
	offset = i % 2;
	for (j=1+offset; j<=N; j+=2)
    {
		S1: temp = A[i] [ j];
		S2: A[i][j] = 0.2 * (A[i][j]+A[i][j-1]+A[i-1][j]+A[i][j+1]+A[i+1][j]);
		S3: diff += abs (A[i][j] - temp);
    }
}

3.6确定变量的范围

①第一步：通过代码分析或算法分析确定并行任务后，就可以并行执行这些并行任务。

通常情况下，并行任务数量多于可用处理器的数量，因此多个任务在分配给线程执行之前经常会合并为较大的任务。执行任务的线程数通常等于或小于可用处理器的数量。在本节中，假设处理器的数量无限，并且为每个任务分配不同的线程。

②第二步：变量分区，这一步确定变量应该具有线程私有作用域还是线程共享作用 域。

这一步是共享存储编程特有的；在消息传递模型中，所有变量都是私有的，因为每个进程都有自己的地址空间。在这一步中，需要通过已经确定的并行任务来分析不同变量的使用，并将其分类到以下行为类别中：

• 只读：变量只由所有任务读取。
• 读/写非冲突：变量只由一个任务读取、写入或既读取又写入；如果变量是矩阵，则其中不同的元素被不同的任务读取/写入。
• 读/写冲突：如果任务并行执行，由一个任务写入的变量可能由不同的任务读取。

读/写冲突变量阻碍并行，因为它引入了线程之间的依赖。因此，这里需要相关的技术来消除这种依赖。

①一种技术就是私有化，私有化为每个读/写冲突变量创建单线程副本，以便每个线程可以单独工作在自己的副本上。

②另一种技术是归约（reduction）,归约为每个读/写冲突变量创建单线程副本，使得每个线程能够在自己的副本中产生部分结果，并且在并行部分的结尾处，所有的部分结果合并成全局结果。

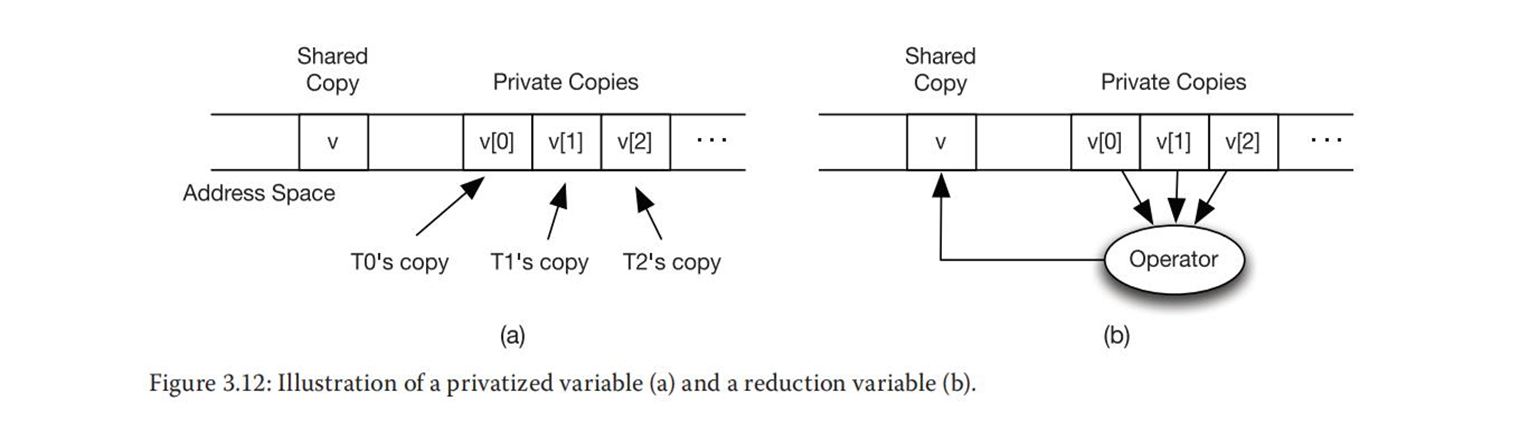
3.7同步

在共享存储模型中，程序员通过同步机制来控制并行线程执行的操作序列。注意同步在线程间而不是任务间执行。所以，在这一步假设任务已经分配给了线程。

① 第一种是两个并行任务的点对点同步，如描述DOACROSS和DOPIPE并行时用到的提交和等待。

②第二种流行的同步是锁。一个锁只能由一个并行线程获得，一旦该线程持有该锁，其他线程将无法获得它，直到当前线程释放该锁。获取锁(lock(name))和释放锁(unlock(name))是在锁上执行的两个操作。因此，本质上讲锁需要保证排他性。

如果一个代码区被一个锁保护，那么可以创建一个临界区，临界区是一个在任何时刻都只允许最多一个线程执行的代码区。临界区对于确保一次只有一个线程访问不可被私有化或归约的读/写冲突变量是有用的。如果一个数据结构受到锁的保护，则一次只能被一个线程访问。

③第三种流行的同步是栅障。栅障定义了一个点，只有在所有线程都到达该点时才允许线程通过。

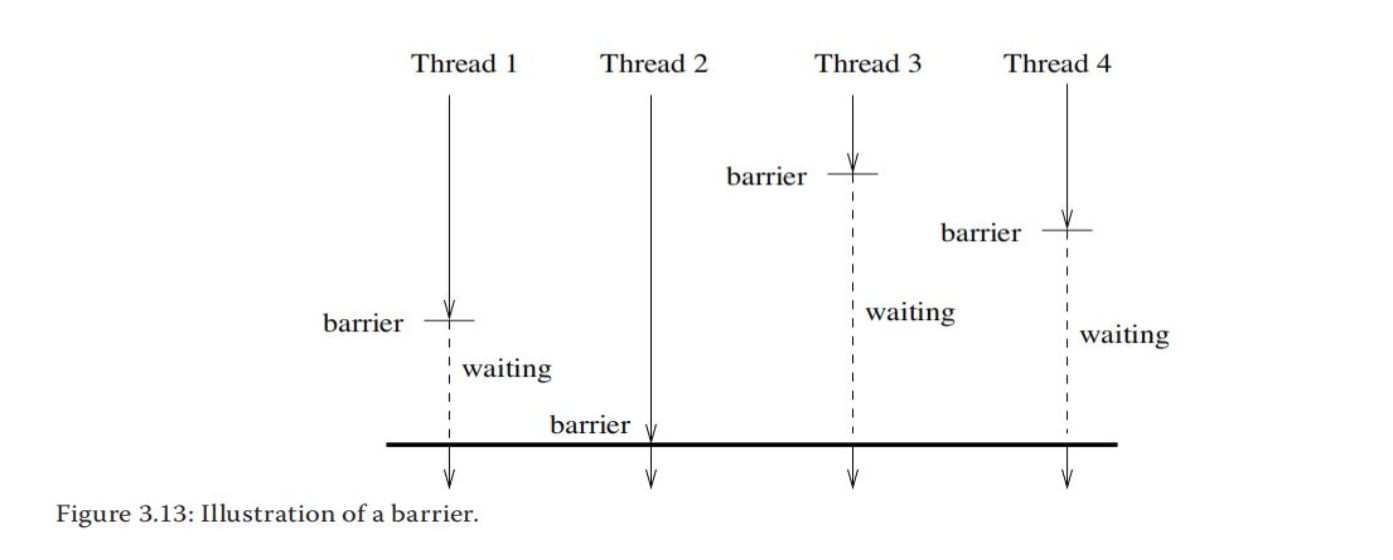
如上图所示，四个线程在不同时间到达栅障点，线程1、3和4必须在栅障内等待直到最后一个线程（线程2）到达。只有这时它们才能执行栅障后的代码。这个例子说明栅障简单易用，它使并行执行的总执行时间取决于最慢线程的执行时间。因此，当使用栅障时，负载均衡是非常重要的。栅障实现的效率也是设计并行计算机的关键目标。

3.8任务到线程的映射

任务映射涉及两个方面：

①如何将任务映射到线程

通常任务比线程更多，这带来了两个问题：哪些任务应该分配给同一个线程，以及如何分配？其中需要解决的问题包括任务管理开销（较大的任务会带来较低的开销）、负载均衡（较大的任务可能会减少负载均衡）以及数据局部性。

②如何将线程映射到处理器，以确保通信的处理器尽可能相互靠近

任务映射的一个考量是静态还是动态地将任务分配给线程。静态任务映射意味着任务在执行之前预先分配给线程。动态任务映射意味着任务在执行之前不会分配给线程。动态任务映射给任务队列管理带来了额外的开销，但有时更容易确保所有线程的负载均衡。动态任务映射往往会增加通信量并减少局部性，因为在编译时不知道数据将由哪个线程使用，因此很难将该数据放置到将要使用它的线程中。最后，也可以采用混合映射，其中映射大部分是静态的，但周期性地评测负载均衡情况，然后相应地调整映射。

负载均衡和任务开销并不是任务映射中唯一重要的因素，通信成本也是一个重要因素。

通信开销分为两种：来自任务映射对算法影响的固有通信和来自任务映射对数据布局方式和架构影响的人为通信。

评估固有通信的一个有用指标是通信-计算比率(CCR)。用线程的通信量除以该线程的计算量。参数是处理器的数量和输入规模。见P63

3.9线程到处理器的映射

解决这个问题的一个简单方法就是什么都不做，即让操作系统线程调度器去决定。

操作系统线程调度器决定何时就绪线程应该运行，以及就绪线程应该运行在哪些处理器上。操作系统将响应时间、公平性、线程优先级、处理器的利用率以及上下文切换的开销考虑在内。

3.10OpenMP概述

OpenMP (开放式多处理)是支持共享存储编程的应用编程接口(API)。

课堂习题：

习题1

注意第二个for循环处：j<=i

答案处的循环传递依赖，笔者一般习惯写为：S1[i,j]→^TS1[i,j+1] //for a （没有本质区别）

(3.4) //for a

(3.5) //for b

(3.6) //for c

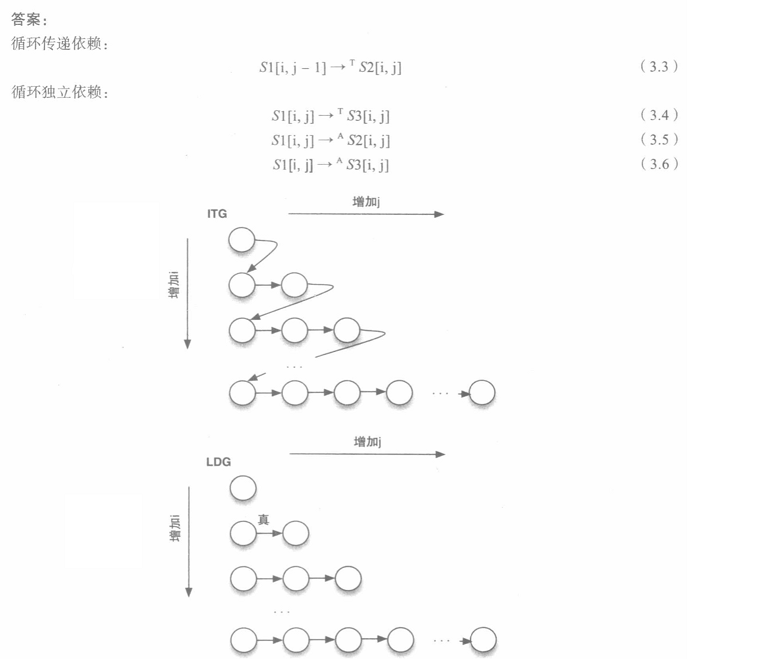
习题2

循环传递依赖：

S1[i,j]→^TS1[i,j+1] //for a

S1[i,j]→^TS1[i,j+2] //for a

(3.11) //for a

(3.12) //for a

习题3

要想并行则不能存在依赖关系，需要进行肉眼判断，显然S4与其他之间不存在依赖关系

DOACROSS代码，signal负责发信号给S2和S3

DOPIPE代码较好记忆，one by one的方式，主要是signal(i,j)和wait(i,j)一一对应。特别的，signal位于主代码后，wait位于主代码前。

习题4

共享越多，通信量越大

课后习题：

重点题目：2,3,4,5,6

习题1

（a）

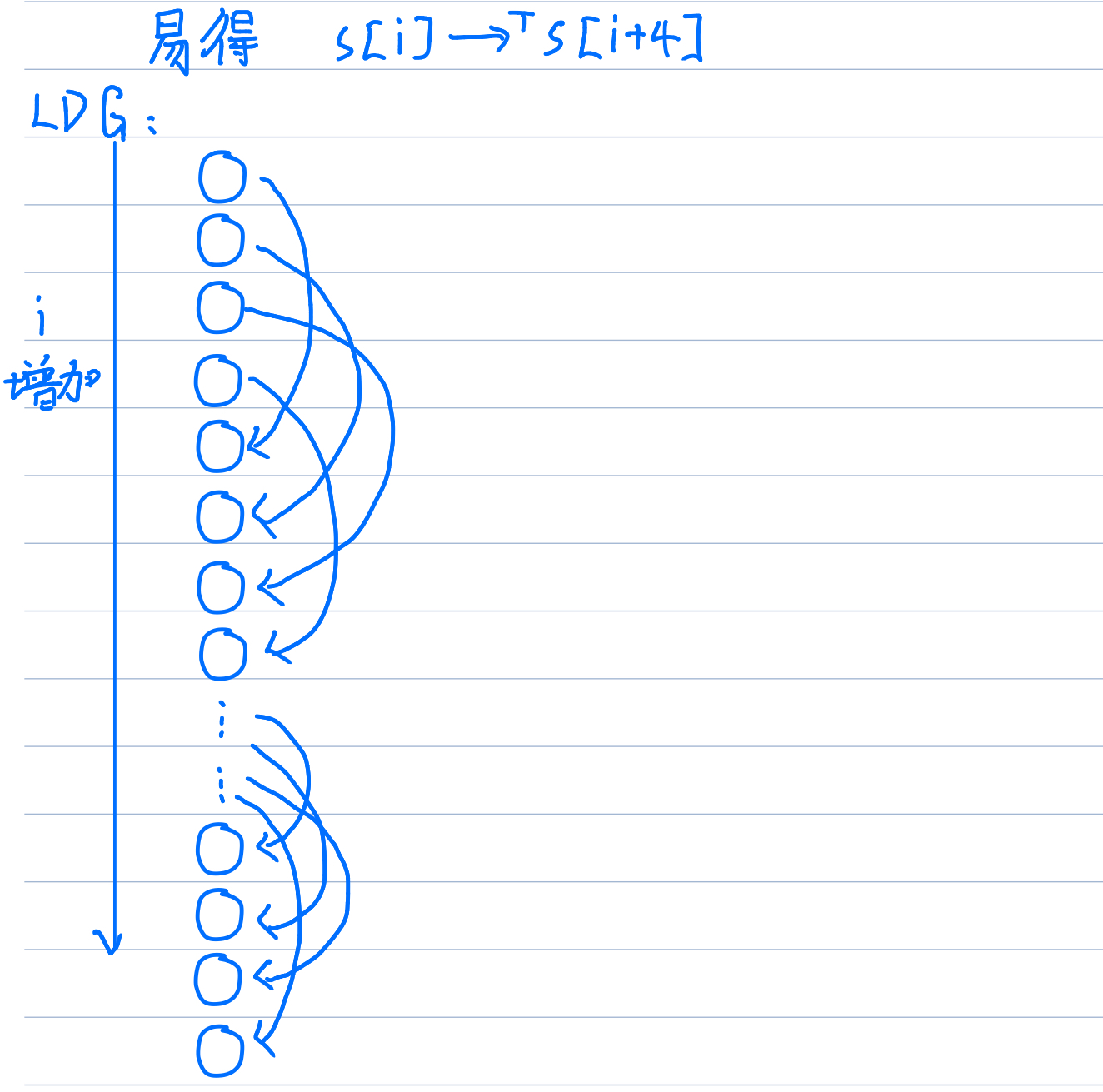
（b）

#progma omp parallel shared(A,n) private(i) section
{
    #progma omp section
	for(i=4;i<=n;i+=4) 
        A[i]=A[i]+A[i-4];
	#progma omp section
	for(i=5;i<=n;i+=4) 
        A[i]=A[i]+A[i-4];
	#progma omp section
	for(i=6;i<=n;i+=4) 
        A[i]=A[i]+A[i-4];
	#progma omp section
	for(i=7;i<=n;i+=4) 
        A[i]=A[i]+A[i-4];
}

习题2

习惯性解决（b），解决后方便画图。

（b）

循环传递依赖：

S1[i, j]→^T S2[i+1, j+1] //for a

循环独立依赖:

S1[i, j]→^T S3[i, j] //for a

S1[i, j]→^A S2[i, j] //for b

S1[i, j]→^A S3[i,j] //for c

（a），（c）

注意内层for循环：j<=i

习题3

习惯性解决（b），解决后方便画图。

（b）

循环传递依赖：

S1[i, j]→^T S2[i+1, j+1] //for a

S3[i-1, j]→^T S1[i, j] //for c

S2[i, j]→^A S2[i+1, j-1] //for b

S3[i-1, j]→^T S2[i+1, j] //for c

循环独立依赖:

S1[i, j]→^T S3[i, j] //for a

S1[i, j]→^A S2[i, j] //for b

（a），（c）

注意内层for循环：j<=i

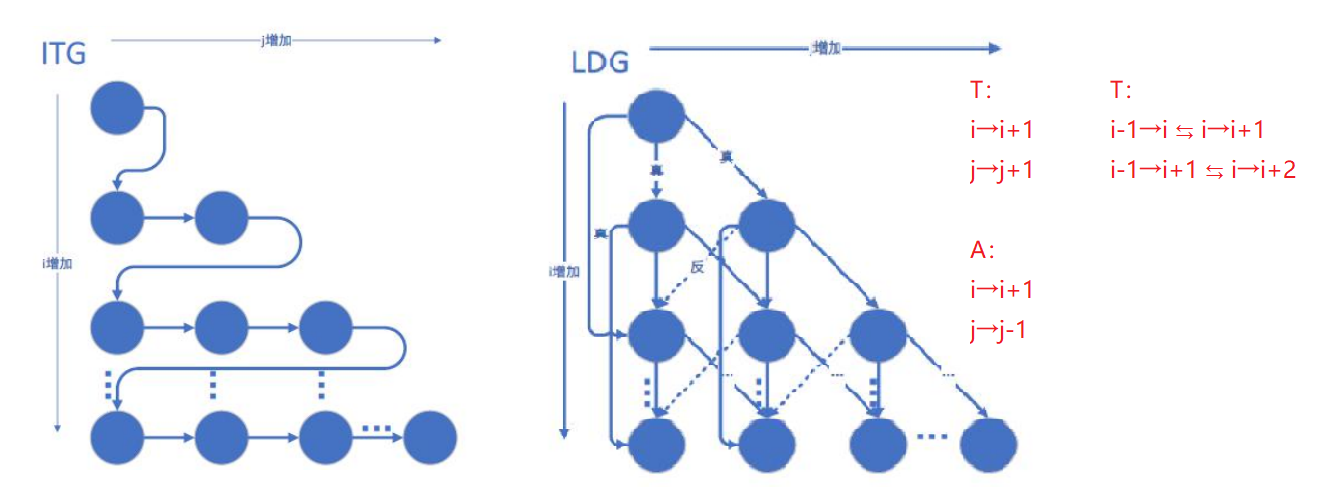
习题4

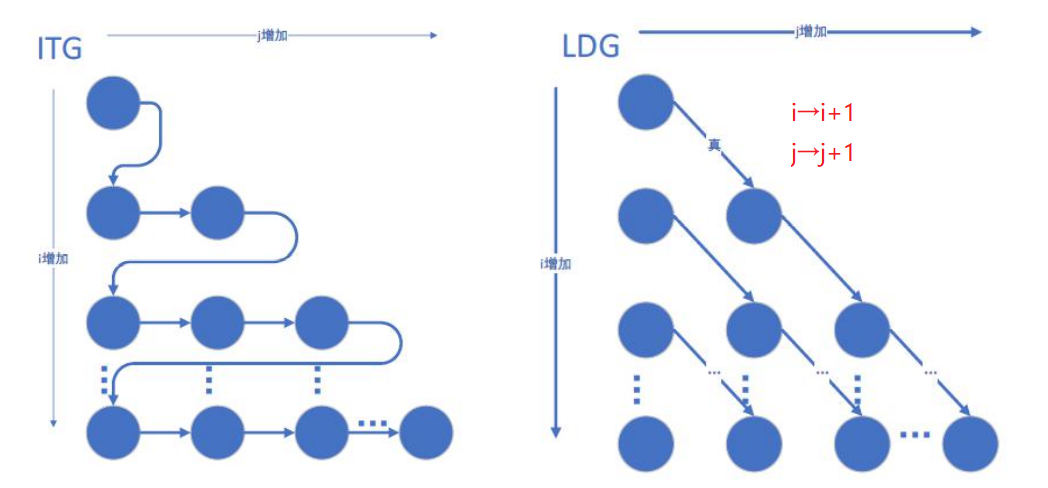
找出所有的依赖：

循环传递依赖：

S[i, j]→^T S2[i, j+2] //for a

S[i, j]→^A S[i+2, j] //for a

ITG：

LDG：

习题5

（a）

signal(1);
for(i=2;i<=N;i++)
{
	wait(i-1);
	S1: a[i]=a[i-1]+b[i-2];
	S2: b[i]=b[i]+1;
	signal(i);
}

（b）

//thread 1
for(i=2;i<=N;i++)
{
	S1: a[i]=a[i-1]+b[i-2];
	signal(i);
}
//thread 2
for(i=2;i<=N;i++)
{
	wait(i-2);
	S2: b[i]=b[i]+1;
}

习题6

for(i=0;i<=N;i++)
{
	k = C[N-1-i];
	for(j=0;j<=N;j++)
    {
        A[i][j] = k*A[i][j]*B[i/2][j];
    }
		
}

仅并行化for i

变量	性质
i	私有变量
k	私有变量
j	私有变量
C	共享变量
B	共享变量
A	共享变量

仅并行化for j

变量	性质
i	共享变量
k	共享变量
j	私有变量
C	共享变量
B	共享变量
A	共享变量

习题7

（a）仅函数并行

#progma omp parallel shared(x,y,rx,ry) private(j,i) sections
{
	#progma omp section
	for (j=2;j<n;j++)
	{
		for(i=2;i<n;i++)
		{
			x[i][j]=x[i][j]+rx[i][j];
		}
	}
	#progma omp section
	for (j=2;j<n;j++)
	{
		for(i=2;i<n;i++)
		{
			y[i][j]=y[i][j]+ry[i][j];
		}
	}
}

（b）仅数据并行

#progma omp parallel for shared(x,y,rx,ry) private(j,i)
{
	for (j=2;j<n;j++)
	{
		for(i=2;i<n;i++)
		{
			x[i][j]=x[i][j]+rx[i][j];
			y[i][j]=x[i][j]+ry[i][j];
		}
	}
}

（c）函数和数据并行

#progma omp parallel shared(x,y,rx,ry) private(j,i) sections
{
	#progma omp section
	#progma omp parallel for
	for (j=2;j<n;j++)
	{
		for(i=2;i<n;i++)
		{
			x[i][j]=x[i][j]+rx[i][j];
		}
	}
	#progma omp section
	#progma omp parallel for
	for (j=2;j<n;j++)
	{
		for(i=2;i<n;i++)
		{
			y[i][j]=y[i][j]+ry[i][j];
		}
	}
}

习题9

#pragma omp parallel for reduction(*: y) default(shared) private(i)
for (i=0;i<n;i++)
	if (x>1 || y>1) y=y*exp(x,A[i]);
print y;