并行多核体系结构基础——第二章知识点和课后习题
本章节主要介绍对并行编程模型的理解、几种广泛运用的并行编程模型和编程模型与体系结构之间的关系。
知识点:
2.1并行程序性能限制因素
从根本上讲,程序员对于以并行方式执行算法或代码的期望是获得比串行算法或代码更短的执行时间。一种分析并行程序执行时间的有用工具是Amdahl定律。(第一章涉及)Amdahl定律表示要获得高可扩展性是困难的,它要求程序的所有部分都几乎可以完全、完美地并行化。那些无法并行的部分必须很少,这样才可能获得可扩展的并行执行性能。
通过增加处理器数量来提升加速比所获得的回报是逐渐递减的,这一点可以从下图看出:
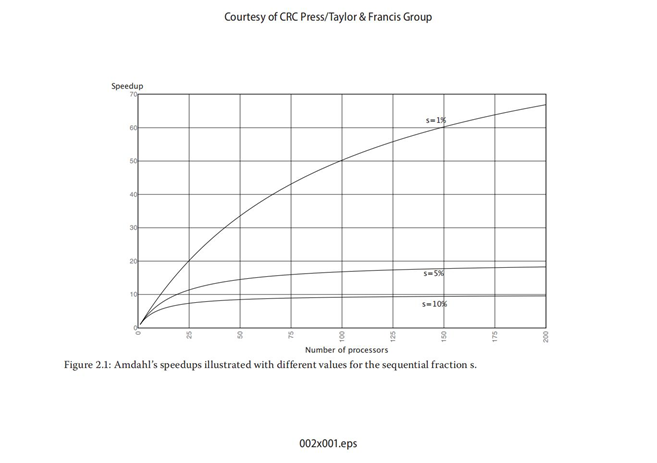
也就是说,处理器个数增加所带来的加速比增长有一个临界值。
串行比例s不是影响加速比的唯一因素。还有一些其他因素会降低加速比,比如负载不均衡、同步开销、通信开销以及线程管理开销。这些因素中的多数开销都会随着处理器个数增加而增大。
从下图中可以看岀,线性增长的开销会导致最大加速比的下降,以及用更少的处理器即能得到最大加速比。在开销以二次方增长时能看到同样的现象。还应当注意到在这些开销下,存在一个加速比最优的线程个数,当线程数超过该值时,加速比会下降。
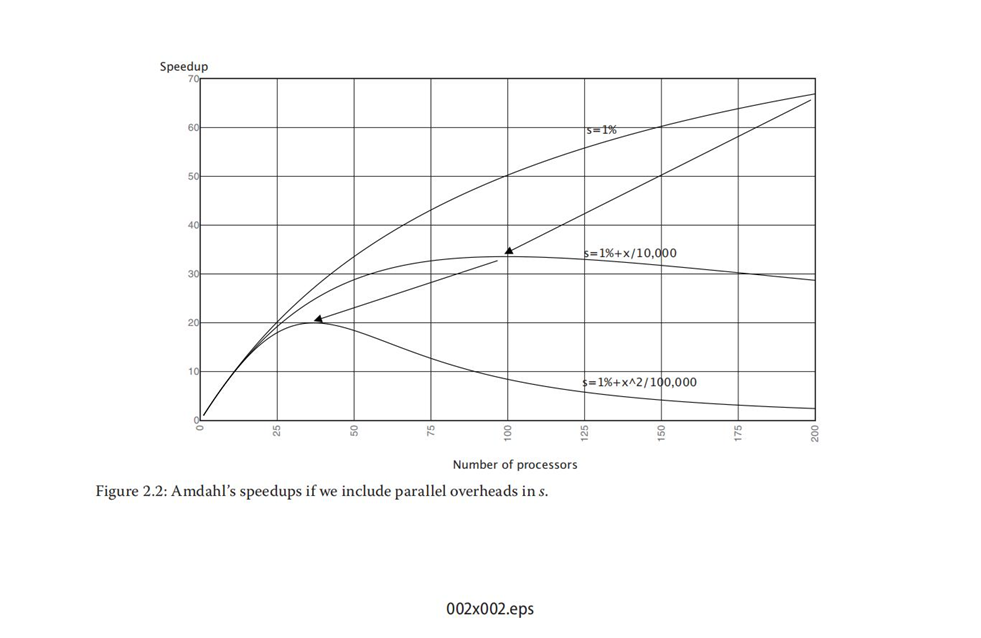
线程个数增长的回报逐渐减少这一现象意味着,通过发掘线程级并行能够收获的性能提升非常有限。当越过拐点后,在一个多核芯片中继续增加核数的做法就不再经济了,因为临界性能收益过小或者是负值。(边际效益)
从能效角度看,线程级并行的能效随着线程个数增长而下降。其原因是,功耗至少会随着处理器个数线性增长,与功耗的增长相比,加速比只会按一个较小的比例增长。因此,功耗-性能比会随着线程个数增长,它等价于能效的下降。仅当加速比能够完美地随线程个数增长时,能效才可以保持住。
两个概念:
①弱可扩展(weak scaling):如果输入集合的大小随线程个数按比例增长,且效率不随着线程数的增大而降低则通常称为弱可扩展。
②强可扩展(strong scaling):如果输入集合的大小是固定的,效率不随着线程数的增大而降低则通常称为强可扩展。
Amdahl定律中存在一个歧义,即一个程序的串行执行时间(T1)的构成。这可以有如下几种选项:
①使用与并行执行相同的并行程序,但以单线程运行在单处理器上。
②该程序的串行版本。
③该程序的最佳串行版本。
采用第一种选项是不正确的。因为串行执行不应当包含并行开销,如线程创建、并行库调用等。
第二种使用程序串行版本的选项更正确一些,因为并行开销没有包含在内。但仍应当注意该选项的一个潜在问题,即所使用串行程序的编程实现是否足够理想。
正确的选项是最后一个,它使用该程序的最佳串行版本来测量,这里所说的“最佳”既指算法层面,也指代码层面。
2.2并行编程模型
两种广泛应用的并行编程模型:共享存储和消息传递。
消息传递模型更多地用于较大型系统(数百到数千核),而共享存储模型更多地用于较小型系统。
把一个并行任务定义为一个计算单元,计算单元间可相互独立执行。多个并行任务可以在不同的处理器(核)上运行。
两种编程模型特性:
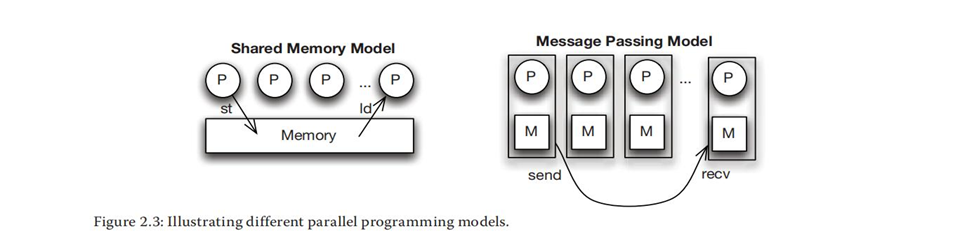
共享存储模型的编程抽象是,不同线程或进程执行的并行任务能够访问内存的任何位置,这样它们可以通过写入(通过store指令)和读取(通过load指令)内存位置实现相互间的隐式通信,这与同属一个进程的多个线程间共享地址空间类似。多用线程实现
消息传递模型中,进程拥有各自的本地内存,一个进程不能访问另一个进程的内存,这样进程间为了交换数据,就需要通过显式地传递包含数据值的消息彼此通信。多用进程实现
线程通信模型:

上述代码所示的线程模型中,同属一个进程的多个线程共享同一地址空间,因此子线程可以自动地知道变量a和b的值,尽管这两个变量的值是由主线程初始化的。然而,在主线程对变量a和b初始化之前,要阻止子线程访问这两个变量,为此使用一个变量signal, 它的值初始设置为0,子线程将等待直到signal的值变为1。最后,在子线程执行完毕之前主线程不能继续运行,因此,主线程一直等待直到signal变量被子线程修改为1。
进程通信模型:

在进程模型中,由于进程的地址空间是私有的,一个子进程无法自动地知道变量a和b的值。如上述代码所示,主进程和子进程之间必须通过显式的发送和接收消息来进行通信。由于进程之间并不共享地址空间,主进程必须发送一条包含变量a和b的消息,该消息必须由子进程接收。
对于线程模型来说,由于不需要用显式的通信来传递数据,避免了通信开销,从这个角度讲这种模型更轻量,但它需要同步来控制不同线程的操作顺序,且线程数量不能太多。
对于进程模型来说,由于需要用显式的通信来传递数据,收发消息的开销难以避免,从这个角度讲这种模型不够轻量,然而从另一方面看,显式的消息收发同时起到了同步两个进程操作顺序的作用,要求任务粒度较大。
(1)共享存储与消息传递模型的对比
下表归纳了共享存储模型和消息传递模型之间的差异:

共享存储模型无须在线程之间传输数据,但需要显式的同步操作来控制线程间访问数据的顺序。
消息传递模型通过发送和接收消息在进程间传输数据,这些通信操作隐式地起到了控制进程间访问数据顺序的同步作用。
OpenMP程序实例:
#include<stdio.h>
#include<omp.h>
int main()
{
#pragma omp parallel for num_threads(4)
for (int i = 0; i < 6; i++)
{
printf("i=%d, thread ID=%d\n", i, omp_get_thread_num());
}
return 0;
}
然而,一旦并行程序编写出来并开始运行,如果程序员希望将其扩展到更多处理器上,数据存放在哪里以及如何排布就会对性能造成显著的影响。
就通信的粒度来说,消息传递模型常用于任务间通信不很频繁且涉及大量数据的情形,而共享存储模型常用于任务间通信更频繁且每次涉及的数据量较小的情形。原因是发送消息的延迟通常较高,这是由于发送时需要将数据组成消息,并在目的端将消息分拆为数据。当消息传递模型更多地用于大型系统(处理器个数更多)时,上述分析就表现得更加突出。这是因为大型系统的通信延迟更大,因而那些善于较少通信、较长消息的编程模型更适合于这类系统。(移动数据不如移动计算)
(2)一个简单的例子 ⭐⭐⭐
假设要在两个处理器上进行矩阵相乘,如下代码,将两个二维矩阵A和B相乘,结果存放到第三个矩阵Y中。
此时,假设在不考虑性能开销和可扩展性的情况下,将矩阵乘的最内层“for k”循环并行化 (实际上将外层“for i”循环并行化的开销会更小)。假设用一个线程执行循环的一半迭代, 用另一个线程执行剩下的一半循环迭代。线程的ID分别为0和1。
矩阵相乘代码:
#define MATRIX_DIM 500
double A[MATRIX_DIM][MATRIX_DIM],B[MATRIX_DIM][MATRIX_DIM],Y[MATRIX_DIM][MATRIX_DIM];
int i, j, k;
for (i=0; i<MATRIX_DIM; i++)
{
for (j=0; j<MATRIX_DIM; j++)
{
Y[i][ j] = 0.0;
for (k=0; k<MATRIX_DIM; k+ + )
{
Y[i] [j] = Y[i] [j] + A[i] [k] * B[k] [j];
} //for k
} //for j
} //for i
矩阵相乘的共享存储代码:
#define MATRIX_DIM 500
double A[MATRIX_DIM][MATRIX_DIM], B[MATRIX_DIM][MATRIX_DIM],Y[MATRIX_DIM][MATRIX_DIM];
int i, j, k, tid;
int kpriv[2], startiter[2], enditer[2];
for (i=0; i<MATRIX_DIM; i++)
{
for (j=0; j<MATRIX_DIM; j + + )
{
Y[i] [ j] = 0.0;
tid = begin_parallel () ; // 创建一个附加线程
startiter[tid] = tid * MATRIX_DIM/2;
enditer[tid] = startiter[tid] + MATRIX_DIM/2;
for (kpriv [tid] =startiter[tid] ; kpriv[tid] <enditer [tid];kpriv[tid] ++)
{
begin_critical ();
Y[i][j] = Y[i][j] + A[i][kpriv[tid]] * B[kpriv[tid]][j];
end_critical ();
} // for k
barrier ();
end_parallel () ; // 结束附加线程
} // for j
} // for i
...
在代码中,首先要定义哪些代码区间需要被多线程执行,以及哪些代码区间只能由一个线程执行。这些并行代码区间用begin_parallel()和end_parallel()分隔开。假定操作系统或线程库负责创建或分配第二个线程,并对不同的线程返回不同的tid,即初始线程(或父线程)得到的返回值为0,而子线程得到的返回值为1。接下来,两个线程要运行循环的不同迭代区间,因此它们需要算出各自的循环下标范围。这通过线程特有(thread-specific)的(startiter和enditer)数据拷贝(其值由tid计算得),以及使用线程特有的循环下标变量kprive来实现,这样,每个线程就可以追踪它自己的当前循环下标。注意,如果使用原来的循环下标变量k,两个线程将会互相修改覆盖对方的k从而造成相互干扰,因此,每一处k都必须替换为其线程私有版本kprive。通过私有变量,线程间不再相互干扰,因为每一个线程使用变量的私有拷贝,如线程0使用kprive[0]而线程1使用kprive[1]。这一转换用术语称为私有化。这些新的变量并不是真正意义上的私有化,像线程不能访问或修改其他线程的私有变量那样。这些新的私有变量仍然在共享存储中,只不过它们的用途是私有的,即在没有bug的程序中,每个线程只访问自己的变量。
循环体使用begin_critical和end_critical包围。两个线程可能同时更新变量Y[i] [j],这样就存在一个可能性,即两个线程读取了相同的旧值,各自生成新值并同时写入新值,导致一个新值覆盖了另一个新值。这种结果称为竞争,它将产生不正确且不可预知的结果。为了避免竞争。一次只能允许一个线程对Y[i] [j]进行读-修改-写。 因此,线程库必须提供相应的原语支持,在上述代码中,假定的原语begin_critical和end_critical,它们用来标出临界区的起始和结束。一个临界区一次只允许一个线程进入,这样,临界区就将执行串行化了,也就是取消了像个线程间的并行性。尽管这样对性能不利,但同时说明,在共享存储并行程序中,为了确保一个计算按照某种顺序执行,需要在代码中显式地插入同步。最后,语句barrier是另一个同步语句,用来确保所有线程都达到该同步点后,才允许任何线程通过该点继续执行。如果后序计算不依赖于先前的并行执行结果,barrier也可省略。
矩阵相乘的消息传递代码:
#define MATRIX_DIM 500
double A[MATRIX_DIM][MATRIX_DIM], B[MATRIX_DIM][MATRIX_DIM],Y[MATRIX_DIM][MATRIX_DIM];
int i, j, k, tid;
int startiter, enditer;
double temp, temp2;
tid = begin_parallel(); //创建一个附加线程
startiter = tid * MATRIX_DIM/2;
enditer = startiter+MATRIX_DIM/2;
if(tid == 0)
{
send(1, A[0][MATRIX_DIM/2-1]..A[MATRIX_DIM-1][MATRIX_DIM-1]);
send(1, B[MATRIX_DIM/2-1][0]..B[MATRIX_DIM-1][MATRIX_DIM-1]);
}
else
{
recv(0, A[0][MATRIX_DIM/2-1]..A[MATRIX_DIM-1][MATRIX_DIM-1]);
recv(0, B[MATRIX_DIM/2-1][0]..B[MATRIX_DIM-1][MATRIX_DIM-1]);
}
for (i=0; i<MATRIX_DIM; i++)
{
for (j=0; j<MATRIX_DIM; j + + )
{
Y[i][j] = 0.0;
temp = Y[i][j];
for(k=startiter;k<enditer;k++)
{
temp = temp + A[i][k]*B[k][j];
}// for k
if(tid == 0)
{
recv(1,&temp2);
Y[i][j] = temp+temp2;
}
else
{
send(0,temp);
}
}//for j
}//for i
end_parallel();
在消息传递程序中,多个进程间不共享同一内存,因此,所有的变量和数据结构在两个进程中都不是同一拷贝。在代码中,假设初始时只有进程拥有矩阵A和B的准确数据。因此,在主进程请求另一个进程执行一部分循环之前,先要把另一个进程计算所需的那部分矩阵数据发送给对方。另一个进程将执行循环迭代的另一班,它需要读取矩阵A的右半部分和矩阵B的下半部分。这样,在子进程开始计算之前,父进程必须发送矩阵A和B的一般(上述代码send部分),同时子进程必须接受父进程发送的一半矩阵(上述代码recv部分)。在矩阵数据传输完毕后,两个线程使用其startiter和enditer值开始各自的计算。矩阵A和B元素相乘结果累加到一个临时变量temp中,在计算结束时,子进程将部分结果发送给主进程。主进程接收这部分结果,并与自身的计算结果合并,写入Y[i] [j]。
上述代码中,假设发送send和接收recv都是阻塞式的,即当消息缓冲区满时,send将阻塞;当等待的消息未到达时,recv将阻塞。因此,send和recv实际上起到了同步两个进程间计算顺序的结果。
(3)其他编程模型
①分区化全局地址空间(PGAS)
它尝试将共享存储和消息传递两种编程模型的优点结合到一起,即消息传递模型的数据局部性(分区)特点和共享存储模型的数据访问便利性特点。
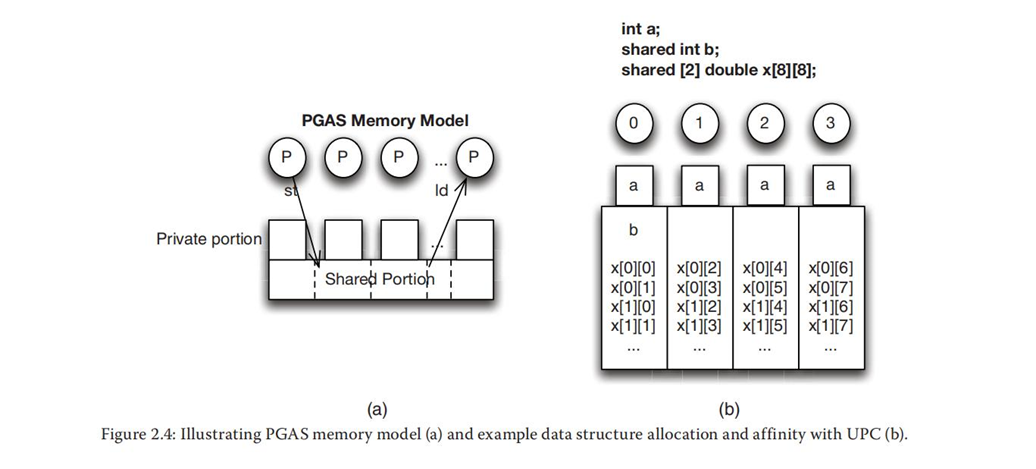
其地址空间包括一个私有部分和一个共享部分。每个线程都分配一个私有部分,该部分只能由线程自己访问,在非一致存储系统结构(NUMA)中,它与线程具有自动的亲和力(affinity)。共享部分则可以被所有线程访问(读和写),这部分被分区为多个具有不同亲和力的区域。数据亲和力定义了数据的分布,即数据应当被分配在共享空间的哪块内存,因此,它可以用于改善局部性,但不能用于限制其他线程访问这些区域。
②数据并行编程模型
数据并行编程模型是一种与单指令流多数据流(SIMD)计算机紧密关联的编程模型

上图给出了一种128位宽的向量寄存器,它能够装入多个数据项,数据项的个数则取决于数据项宽度:两个64位数据项、4个32位数据项、8个16位数据项或16个8位数据项。
③MapReduce
在MapReduce编程中,程序员提供(最少)两个函数:map()和reduce(),它们将在不同的阶段执行。在map阶段,map函数处理输入数据并生成中间结果,中间结果的形式是<key, value〉对的列表。在reduce阶段,reduce函数读取这些key-value对,将那些key值相同的value值规约到一起。
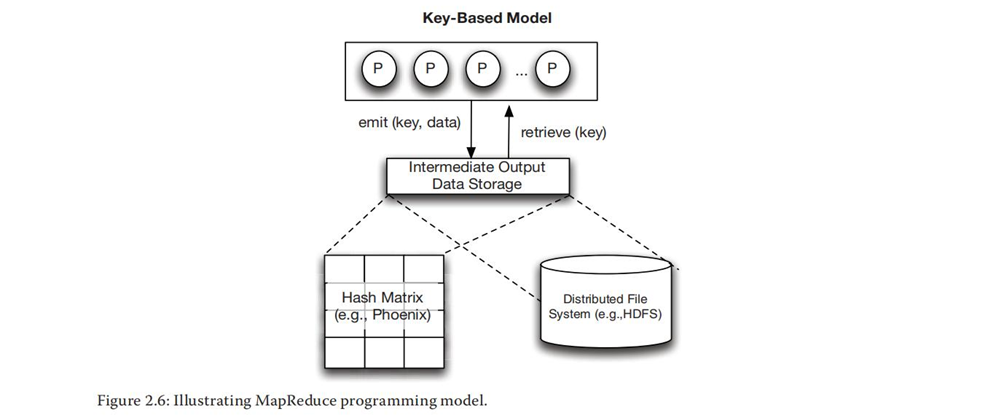
MapReduce编程模型的主要特性是,数据不是直接通过位置访问的,数据的位置被抽象了,map阶段使用key值将数据存入中间结果,并在reduce阶段使用key值从中间结果中提取。
MapReduce的另一个重要特性是它允许的并行性类型。
④事务内存
事务内存(Transactional Memory, TM)是一种编程模型,它允许程序员将一段代码定义为一个事务。事务的概念来源于数据库编程。在数据库中,一个事务必须具备ACID特性,即原子性(atomicity)、一致性(consistency)、隔离性(isolation)和持久性(durability)。
TM提供的是乐观并发性(optimistic concurrency),即线程遇到事务时,将继续执行代码块而不是阻。
课后作业

(a)消息传递
int i,j,k,tid;
float A[n][m],B[m][p],Y[n][p],C[n][p],x;
...
tid = begin_parallel();
start = tid*n/2;
end = start+n/2;
if(tid==0)
{
send(1,A[n/2-1][0]...A[n-1][m-1]);
send(1,B[0][0]...B[m-1][p-1]);
send(1,C[n/2-1][0]...C[n-1][p-1]);
}
else
{
recv(0,A[n/2-1][0]...A[n-1][m-1]);
recv(0,B[0][0]...B[m-1][p-1]);
recv(0,C[n/2-1][0]...C[n-1][p-1]);
}
for(i=start;i<end;i++)
{
for(j=0;j<p;j++)
{
x=0;
for(k=0;k<m;k++)
{
x = x+A[i][k]*B[k][j];
}
Y[i][j] = x+C[i][j];
}
if(tid==0)
{
recv(1,Y[n/2][0]...Y[n-1][p-1]);
}
else
{
send(0,Y[n/2][0]...Y[n-1][p-1]);
}
}
end_parallel();
(b)共享存储
int i,j,k,tid;
float A[n][m],B[m][p],Y[n][p],C[n][p],x;
int ipriv[2],statr[2],end[2];
...
tid = begin_parallel();
start[tid]=tid*n/2;
end[tid]=start[tid]+n/2;
for(ipriv[tid]=start[tid];ipriv[tid]<end[tid];ipriv[tid]++)
{
for(j=0;j<p;j++)
{
x=0;
for(k=0;k<m;k++)
{
x = x+A[ipriv[tid]][k]*B[k][j];
}
begin_critical();
Y[ipriv[tid]][j] = x+C[ipriv[tid]][j];
end_critical();
barrier();
}
}
end_parallel();
自行拓展
以矩阵相乘为例。Y=A*B
#define N 500
double A[N][N],B[N][N],Y[N][N];
int i, j, k;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
{
Y[i][j] = 0.0;
for(k=0; k<N; k++)
{
Y[i] [j] = Y[i] [j] + A[i] [k] * B[k] [j];
} //for k
} //for j
} //for i
矩阵相乘的共享存储代码:
① for k
#define N 500
double A[N][N], B[N][N],Y[N][N];
int i, j, k, tid;
int kpriv[2], start[2], end[2];
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
{
Y[i][j] = 0.0;
tid = begin_parallel () ; // 创建一个附加线程
start[tid] = tid * N/2;
end[tid] = start[tid] + N/2;
for (kpriv[tid]=start[tid]; kpriv[tid]<end[tid]; kpriv[tid]++)
{
begin_critical ();
Y[i][j] = Y[i][j] + A[i][kpriv[tid]] * B[kpriv[tid]][j];
end_critical ();
} // for k
barrier();
end_parallel(); // 结束附加线程
} // for j
} // for i
②for i
#define N 500
double A[N][N],B[N][N],Y[N][N];
int i, j, k, tid;
int ipriv[2], statr[2], end[2];
Y[i][j] = 0.0;
tid = begin_parallel(); //创建一个附加线程
start[tid] = tid * N/2;
end[tid] = start[tid] + N/2;
for(ipriv[tid]=start[tid]; ipriv[tid]<end[tid]; ipriv[tid]++)
{
for(j=0;j<N;j++)
{
for(k=0;k<N;k++)
{
begin_critical();
Y[ipriv[tid]][j] += A[ipriv[tid]][k] * B[k][j];
end_critical();
}
barrier();
}
}
end_parallel(); // 结束附加线程
③for j
#define N 500
double A[N][N],B[N][N],Y[N][N];
int i, j, k, tid;
int jpriv[2], statr[2], end[2];
for(i=0;i<N;i++)
{
Y[i][j] = 0.0;
tid = begin_parallel(); //创建一个附加线程
start[tid] = tid * N/2;
end[tid] = start[tid] + N/2;
for(jpriv[tid]=start[tid]; jpriv[tid]<end[tid]; jpriv[tid]++)
{
for(k=0;k<N;k++)
{
begin_critical();
Y[i][jpriv[tid]] += A[i][k] * B[k][jpriv[tid]];
end_critical();
}
barrier();
}
end_parallel(); // 结束附加线程
}
矩阵相乘的消息传递代码:
①for k
#define N 500
double A[N][N], B[N][N],Y[N][N];
int i, j, k, tid;
int start, end;
double temp, temp2;
tid = begin_parallel(); //创建一个附加线程
start = tid * N/2;
end = start + N/2;
if(tid == 0)
{
send(1, A[0][N/2-1]..A[N-1][N-1]);
send(1, B[N/2-1][0]..B[N-1][N-1]);
}
else
{
recv(0, A[0][N/2-1]..A[N-1][N-1]);
recv(0, B[N/2-1][0]..B[N-1][N-1]);
}
for (i=0; i<N; i++)
{
for (j=0; j<N; j + + )
{
Y[i][j] = 0.0;
temp = Y[i][j];
for(k=start;k<end;k++)
{
temp = temp + A[i][k]*B[k][j];
}// for k
if(tid == 0)
{
recv(1,&temp2);
Y[i][j] = temp+temp2;
}
else
{
send(0,temp);
}
}//for j
}//for i
end_parallel();
②for i
#define N 500
double A[N][N], B[N][N],Y[N][N];
int i, j, k, tid;
int start, end;
double temp, temp2;
tid = begin_parallel(); //创建一个附加线程
start = tid * N/2;
end = start + N/2;
if(tid == 0)
{
send(1, A[0][N/2-1]..A[N-1][N-1]);
send(1, B[N/2-1][0]..B[N-1][N-1]);
}
else
{
recv(0, A[0][N/2-1]..A[N-1][N-1]);
recv(0, B[N/2-1][0]..B[N-1][N-1]);
}
Y[i][j] = 0.0;
temp = Y[i][j];
for (i=start; i<end; i++)
{
for (j=0; j<N; j++)
{
for(k=0;k<N;k++)
{
temp = temp + A[i][k]*B[k][j];
}
if(tid == 0)
{
recv(1,&temp2);
Y[i][j] = temp+temp2;
}
else
{
send(0,temp);
}
}
}
end_parallel();
③for j
#define N 500
double A[N][N], B[N][N],Y[N][N];
int i, j, k, tid;
int start, end;
double temp, temp2;
tid = begin_parallel(); //创建一个附加线程
start = tid * N/2;
end = start + N/2;
if(tid == 0)
{
send(1, A[0][N/2-1]..A[N-1][N-1]);
send(1, B[N/2-1][0]..B[N-1][N-1]);
}
else
{
recv(0, A[0][N/2-1]..A[N-1][N-1]);
recv(0, B[N/2-1][0]..B[N-1][N-1]);
}
for (i=0; i<N; i++)
{
Y[i][j] = 0.0;
temp = Y[i][j];
for (j=start; j<end; j++)
{
for(k=0;k<N;k++)
{
temp = temp + A[i][k]*B[k][j];
}
if(tid == 0)
{
recv(1,&temp2);
Y[i][j] = temp+temp2;
}
else
{
send(0,temp);
}
}
}
end_parallel();

 对并行编程模型的浅理解
对并行编程模型的浅理解

