稳定匹配 - Stable Matching
鉴于网络导论书上本章节稳定匹配内容以研究生与导师双选为例,文字理解起来较为绕,故转载本文用以理解该算法。
这篇文章将会对稳定匹配算法进行图文介绍及Python代码的实现,第一部分会针对稳定匹配的Gale-Shapley算法进行解析,第二部分就是用Python对该算法进行实现。
1、稳定匹配算法原理
1.1、介绍
稳定匹配(Stable Matching)问题就是假设现在有N个男生和N个女生跳舞选择伴侣,然后最开始的时候男、女生按照下面情况对彼此进行排序选择舞伴(见图1):
- 每个男生都对女生按照最喜欢到最不喜欢进行排序;
- 同样的,女生也是按照最喜欢的到最不喜欢对男生进行排序。
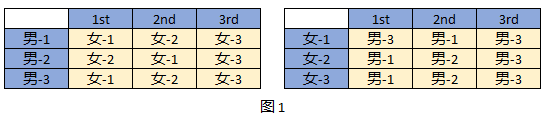
算法目标:每个男生都找到唯一一个女舞伴,反之亦如此,从而达到了所谓的稳定匹配。
演示步骤:
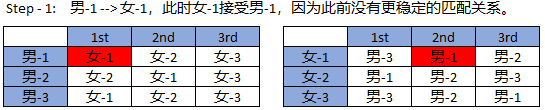
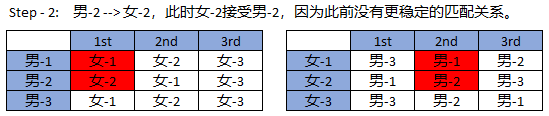
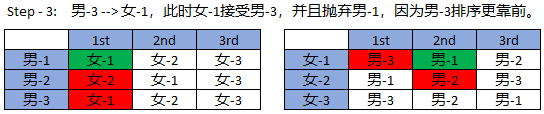
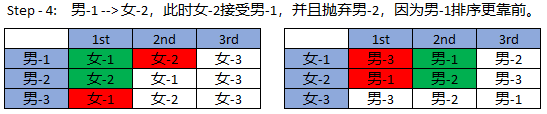
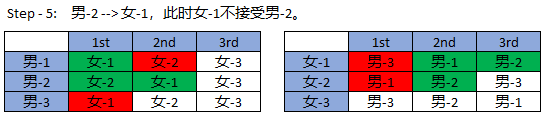
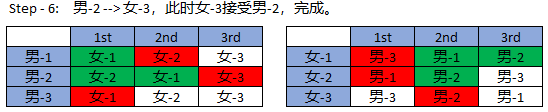
1.2、Gale-Shapley Algorithm
# 首先初始化所有男生的状态为自由
initialize each person to be free
# 当男生没有未曾被匹配过并且也没有向所有其他女生寻求舞伴过时不断循环
while some man m is not yet matched:
# 每个男生按照对女生的喜欢程度选择舞伴
w := m's most favroite woman to whom he has not yet proposed
# 如果女生未被匹配到,则与男生进行配对
if w is also not yet matched:
w and m are paired
# 如果女生与已匹配的男生相比更喜欢当前的这个男生,则拆散重新匹配
elif w favors m to her current matched m':
w and m are paired and m' is dis-matched
# 否则该女生拒绝成为男生的舞伴
else:
w rejects m
# 返回所有匹配成功的舞伴对
return matched pairs
2、Python代码实现
import copy
# 男的所期望的对象
manPrefers = dict((m, prefs.split(', ')) for [m, prefs] in (line.rstrip().split(': ')
for line in open('men.txt')))
# 女的所期望的对象
womenPrefers = dict((m, prefs.split(', ')) for [m, prefs] in (line.rstrip().split(': ')
for line in open('women.txt')))
men = sorted(manPrefers.keys())
women = sorted(womenPrefers.keys())
# 定义检测函数检测匹配的伴侣是否稳定
def check(engaged):
inverseengaged = dict((v,k) for k,v in engaged.items())
for w, m in engaged.items():
shelikes = womenPrefers[w]
shelikesbetter = shelikes[:shelikes.index(m)]
helikes = manPrefers[m]
helikesbetter = helikes[:helikes.index(w)]
for man in shelikesbetter:
womenOftheMan = inverseengaged[man]
manLoves = manPrefers[man]
if manLoves.index(womenOftheMan) > manLoves.index(w):
print("%s 和 %s 更喜欢彼此相比起他们当前的伴侣: %s 和 %s" % (w, man, m, womenOftheMan))
return False
for woman in helikesbetter:
manOfTheWomen = engaged[woman]
womanLoves = womenPrefers[woman]
if womanLoves.index(manOfTheWomen) > womanLoves.index(m):
print("%s 和 %s 更喜欢彼此相比起他们当前的伙伴:%s 和 %s" % (m, woman, w, manOfTheWomen))
return False
return True
def stableMatching():
free_men = men[:]
engaged = {}
manPref_temp = copy.deepcopy(manPrefers)
womenPref_temp = copy.deepcopy(womenPrefers)
while free_men:
man = free_men.pop(0)
manList = manPref_temp[man]
woman = manList.pop(0)
fiance = engaged.get(woman)
if not fiance:
engaged[woman] = man
print(" %s 和 %s 成为伴侣" % (man, woman))
else:
womenList = womenPref_temp[woman]
if womenList.index(fiance) > womenList.index(man):
engaged[woman] = man
print(" %s 舍弃 %s 而和 %s 成为伴侣" % (woman, fiance, man))
if manPref_temp[fiance]:
free_men.append(fiance)
else:
if manList:
free_men.append(man)
return engaged
if __name__ == '__main__':
print('\n伴侣匹配:')
engaged = stableMatching()
print('\n伴侣匹配:')
print(' ' + ',\n '.join('%s 和 %s 成为伴侣' % couple for couple in sorted(engaged.items())))
print()
print('伴侣稳定性检测通过' if check(engaged) else '伴侣稳定性检测不通过')
print('\n\n因交换而产生伴侣搭配错误')
engaged[women[0]], engaged[women[1]] = engaged[women[1]], engaged[women[0]]
for woman in women[:2]:
print(' %s 现在和 %s 成为伴侣' % (woman, engaged[woman]))
print()
print('伴侣稳定性检测通过' if check(engaged) else '伴侣稳定性检测不通过')
3、结论
此处回归研究生S与导师P双选的案例。
- G-S算法在至多N2次迭代后终止,且算法终止时所得到的集合是一个完全匹配
证明如下:

- G-S算法终止时所得到的集合Ω一定是一个稳定匹配
证明如下:

-
公平性,G-S算法所有的执行得到的都是对学生满意、对教师最不理想的稳定匹配
-
稳定匹配的前提条件:每一个学生与每一个老师之间必须具有配对的可能性
-
一个左右节点数相同的二分图存在完全匹配的充要条件是它不包含抑制集, 即存在抑制集是不存在完全匹配的唯一理由
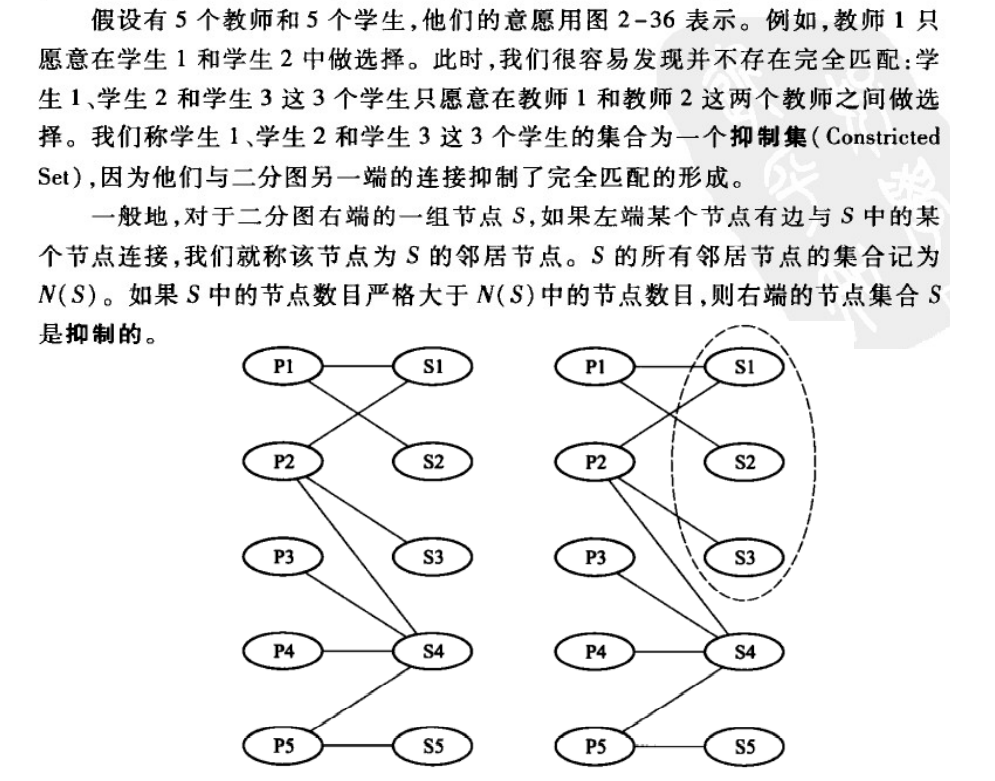

 稳定匹配算法的了解
稳定匹配算法的了解

