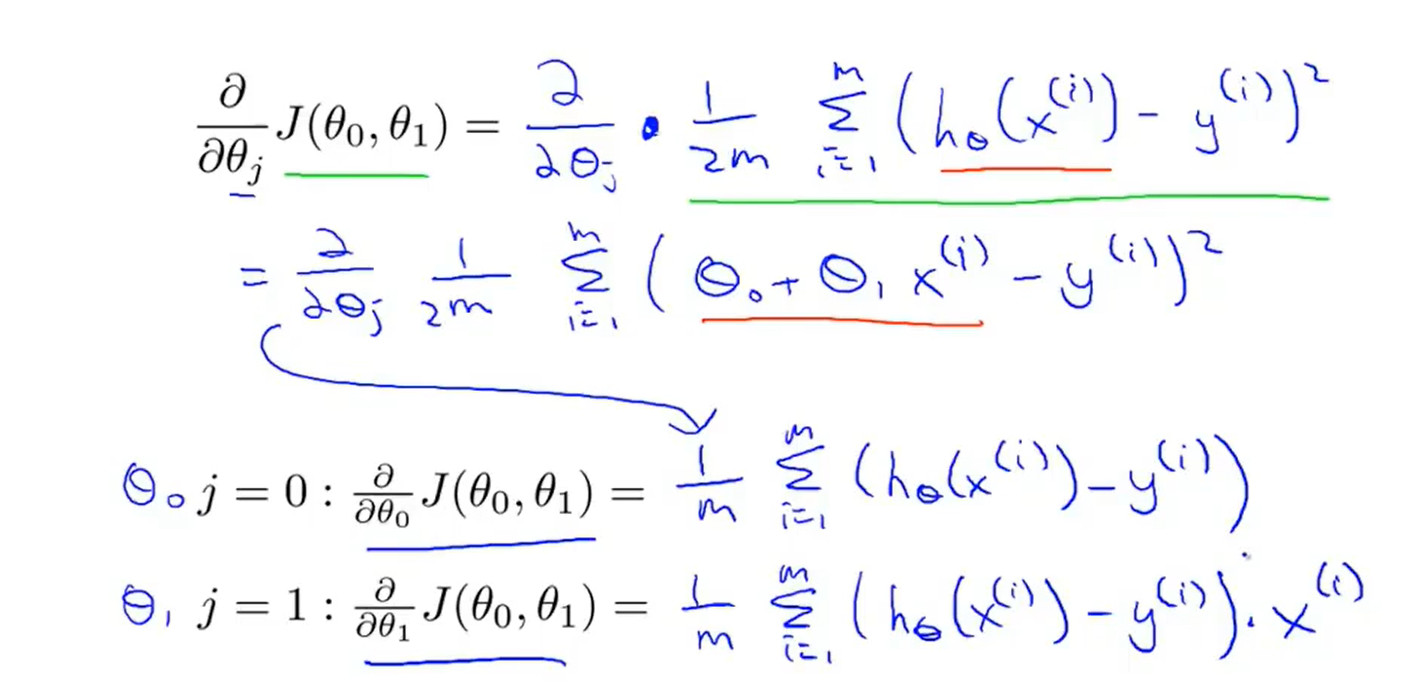Machine learning(2-Linear regression with one variable )
1、Model representation
- Our Training Set [训练集]:
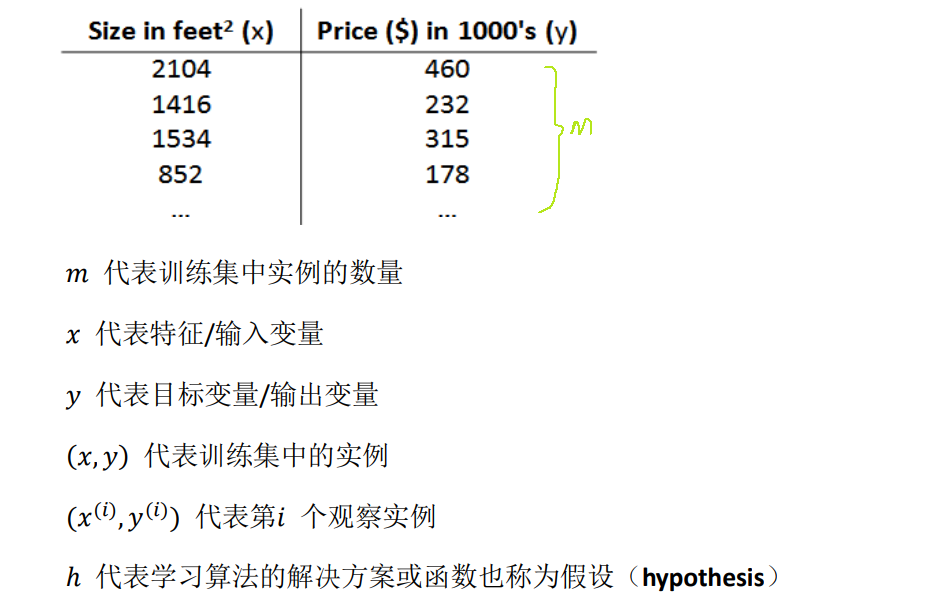
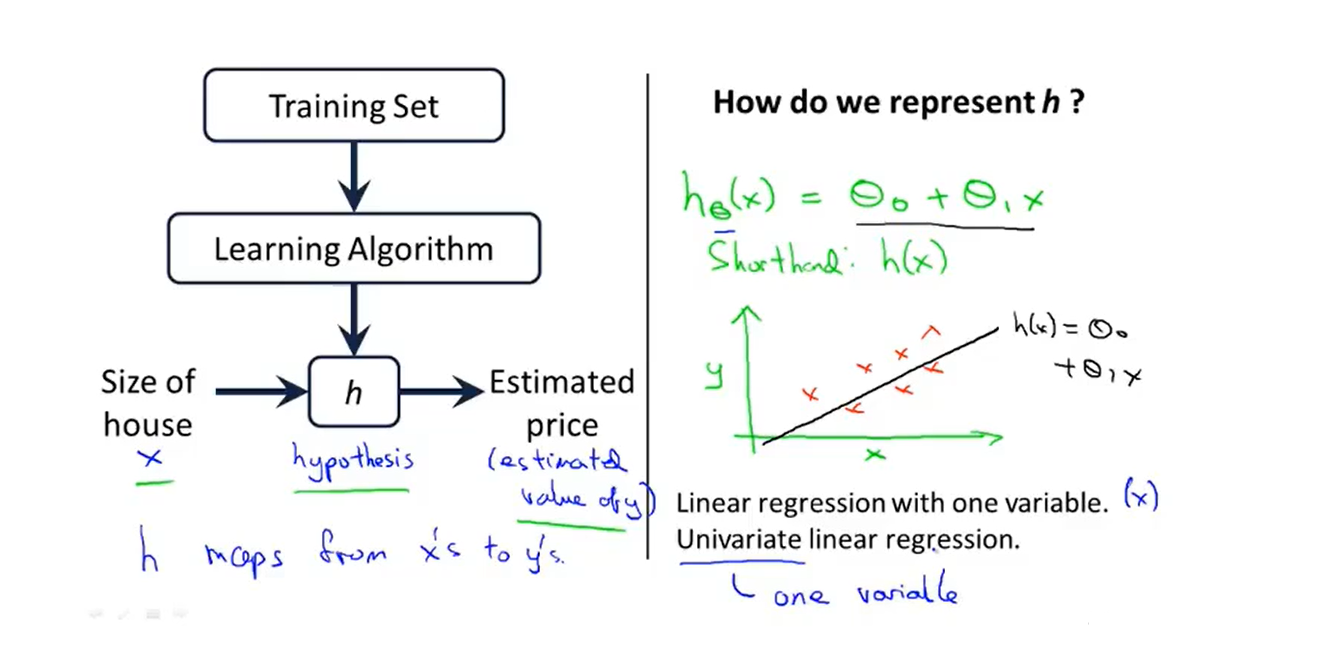
- We will start with this ‘’Housing price prediction‘’ example first of fitting linear functions, and we will build on this to eventually have more complex models
2、Cost function
- 代价函数(平方误差函数):It figures out how to fit the best possible straight line to our data
- So how to choose θi's ?

- and just try:
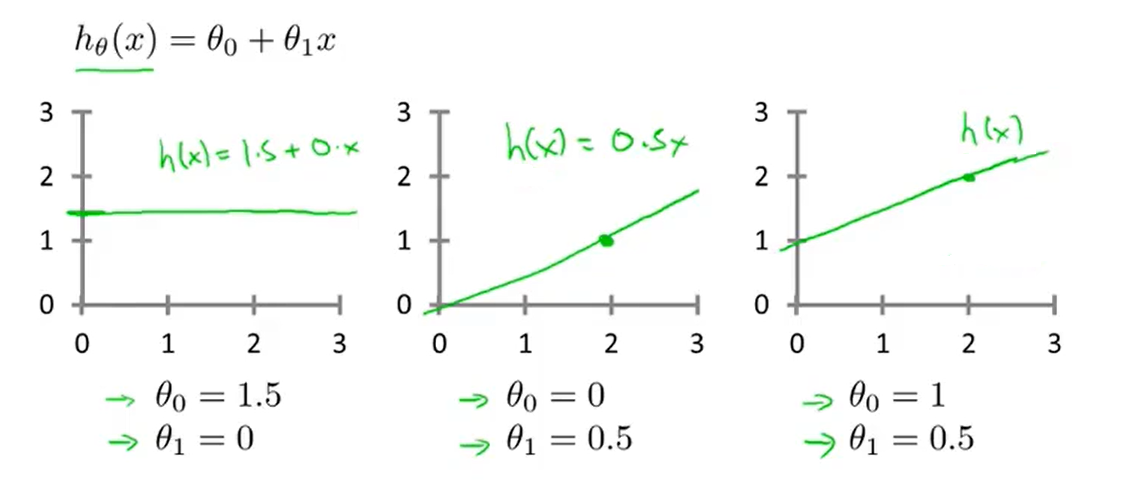
- The parameters we choose determine the accuracy of the straight line we get relative to our training set
- But there is modeling error 建模误差
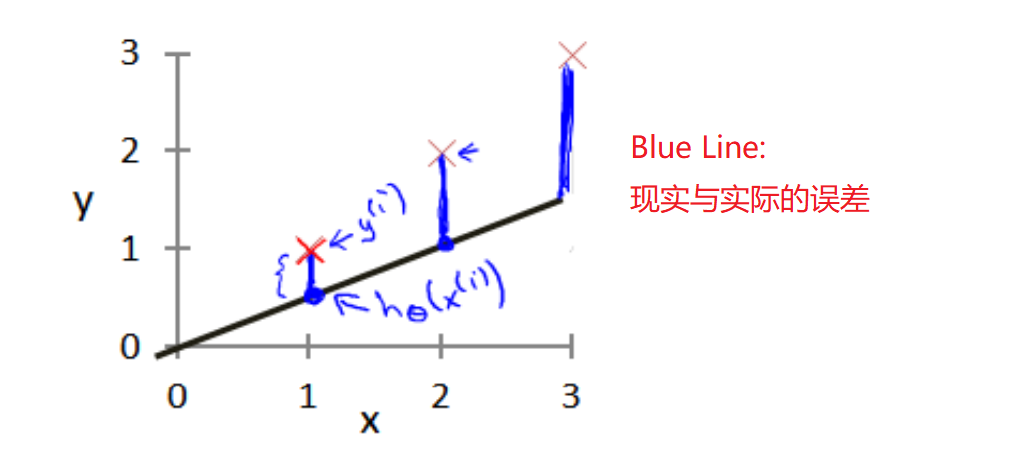
-
Our goal is to select the model parameters that minimize the sum of squares of modeling errors
-
That is to minimize the cost function!
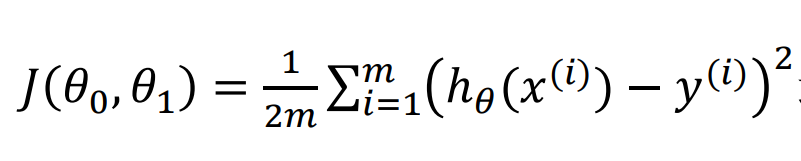
-
summary:

2-1、Cost function introduction I
- We look up some plots to understand the cost function
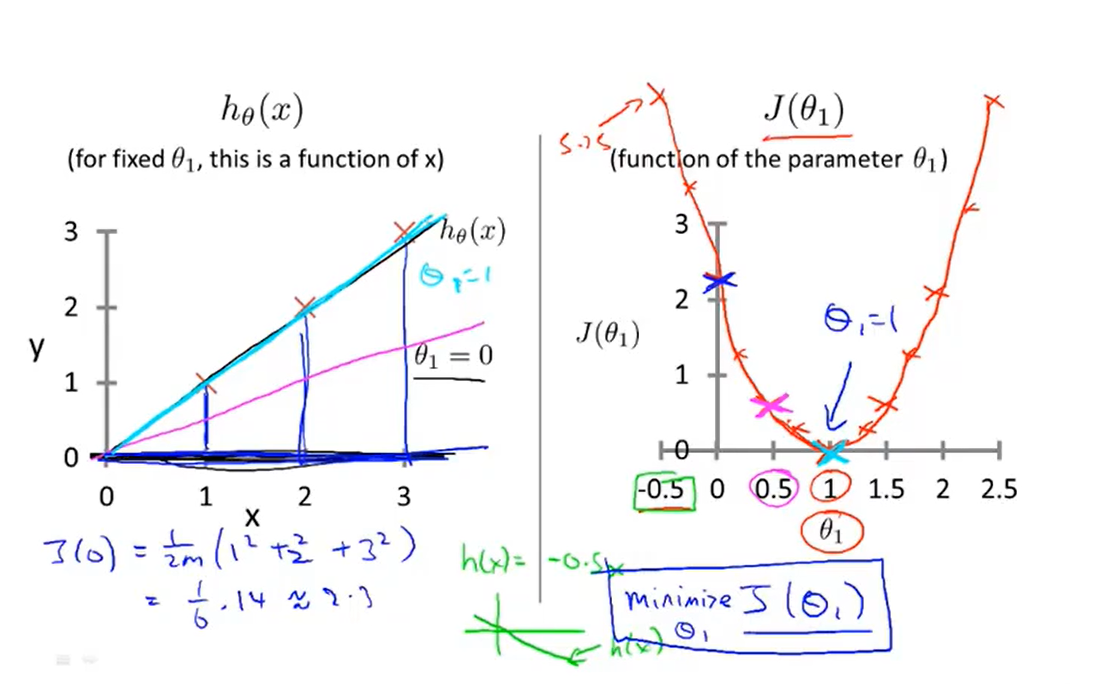
2-2、Cost function introduction II
- Let's take a look at the three-dimensional space diagram of the cost function(also called a convex function 凸函数)
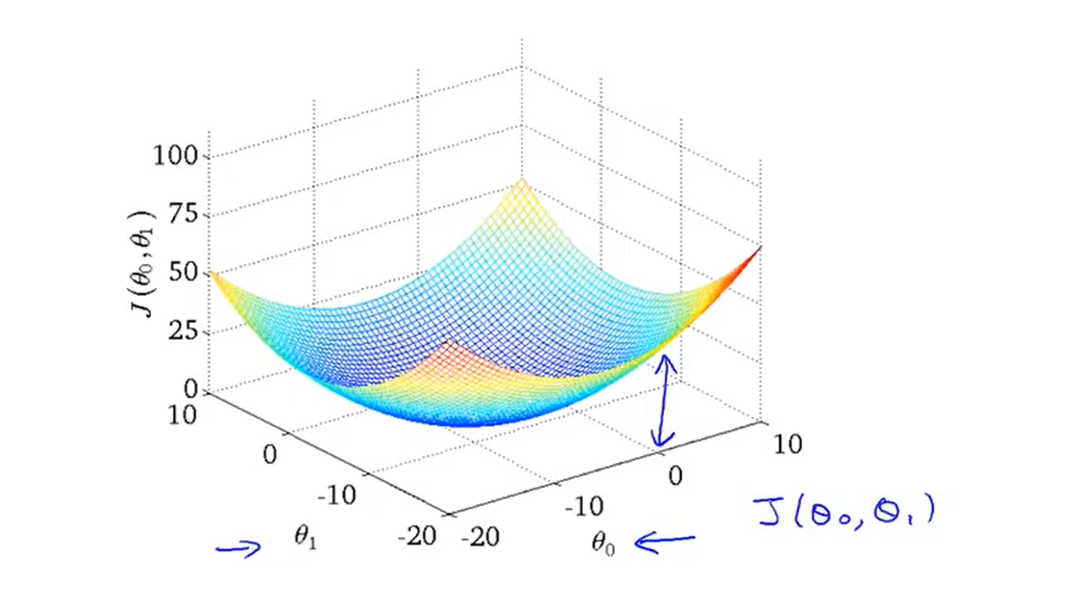
- And here is an example of a contour figure:
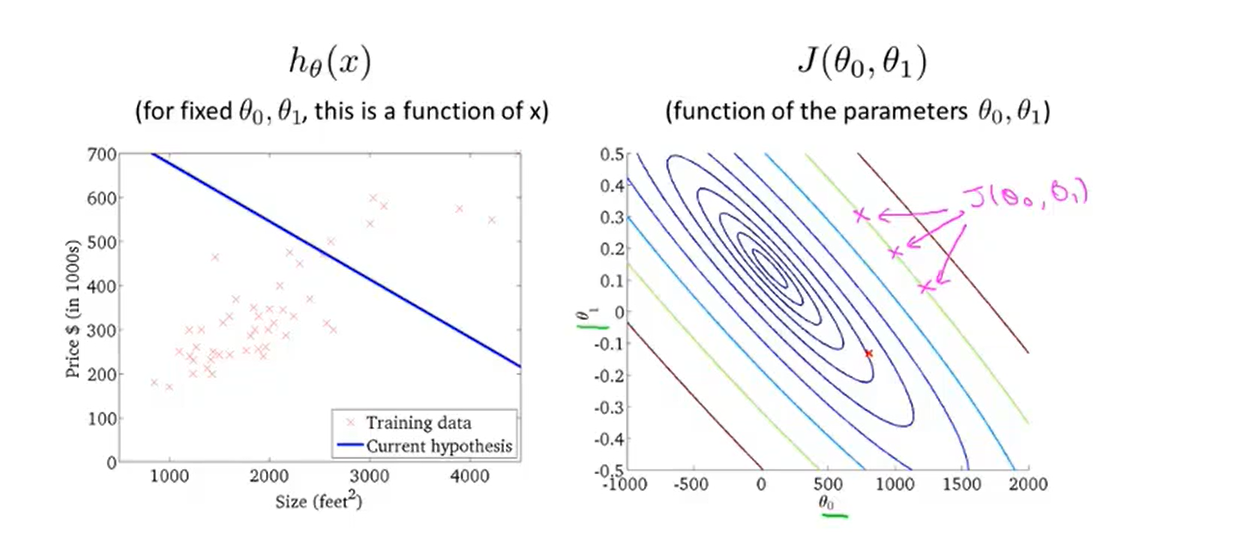
- The contour figure is a more convenient way to visualize the cost function
3、Gradient descent
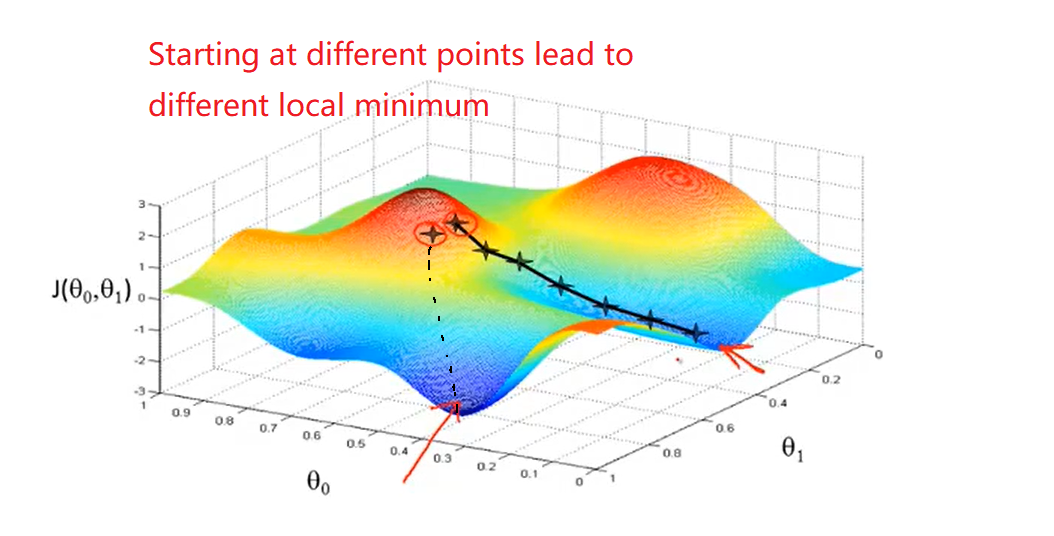
- It turns out gradient descent(梯度下降) is a more general algorithm and is used not only in linear regression. I will introduce how to use gradient descent for minimizing some arbitrary function J

- The formula of the batch gradient descent algorithm :

4、Gradient descent intuition
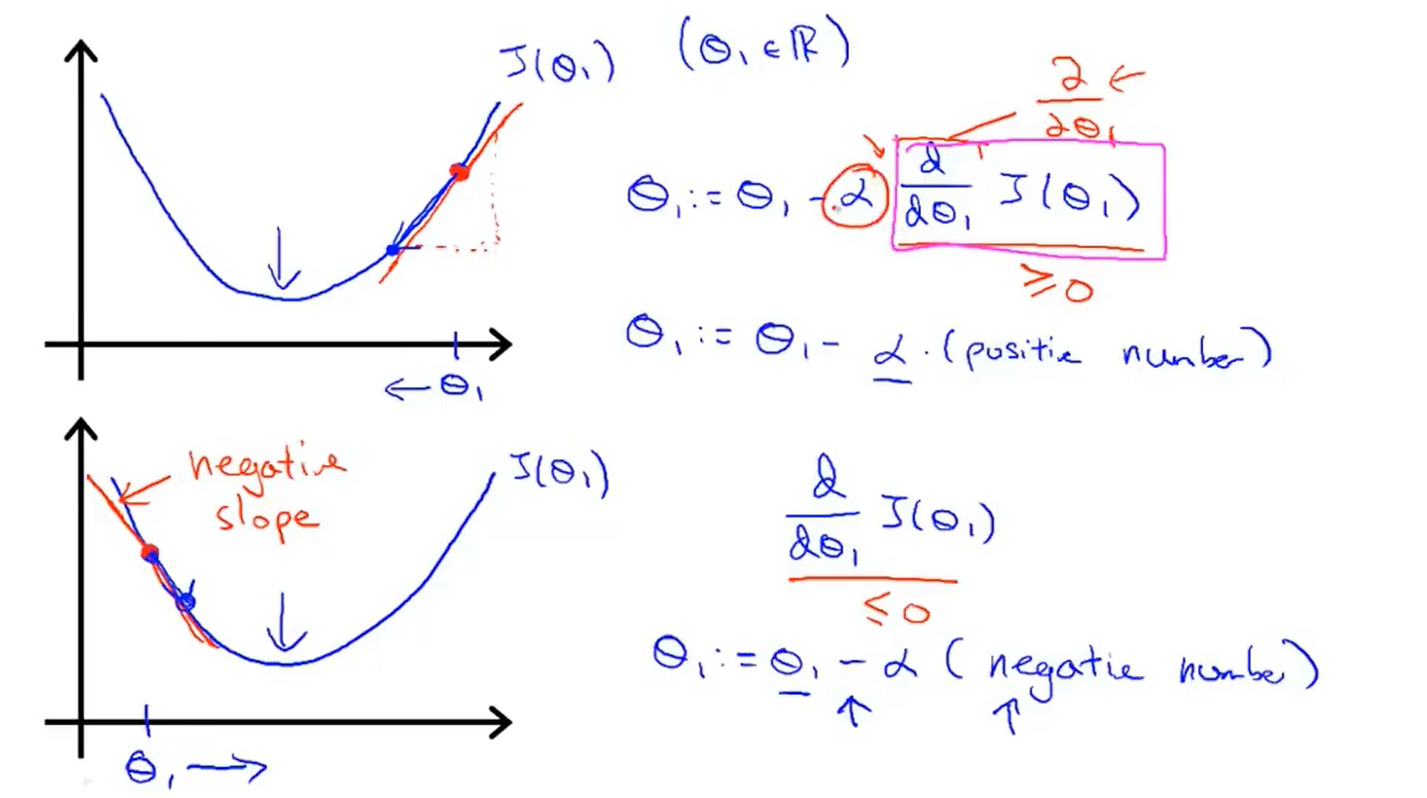
-
Derivative term purpose :get closer to the minimum
-
-
Learning rate α :
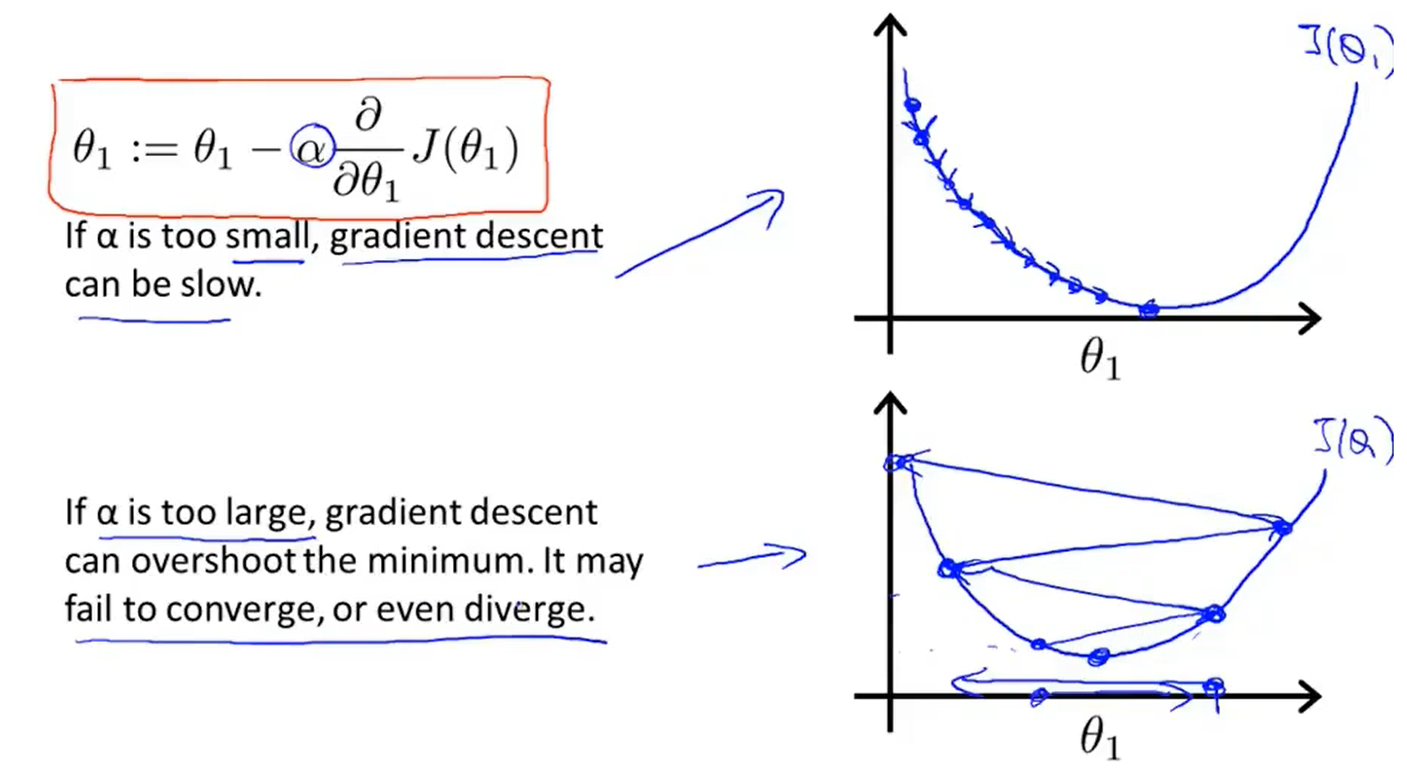
- But what if my parameter θ1 is already at a local minimum?
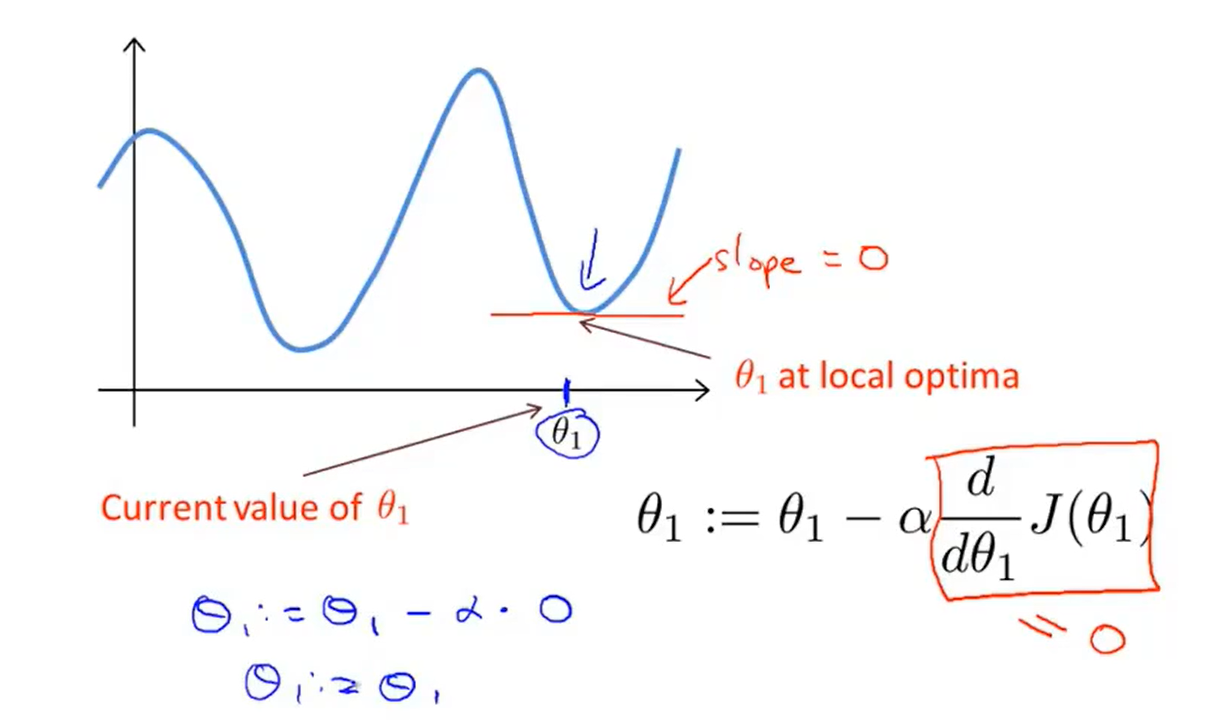
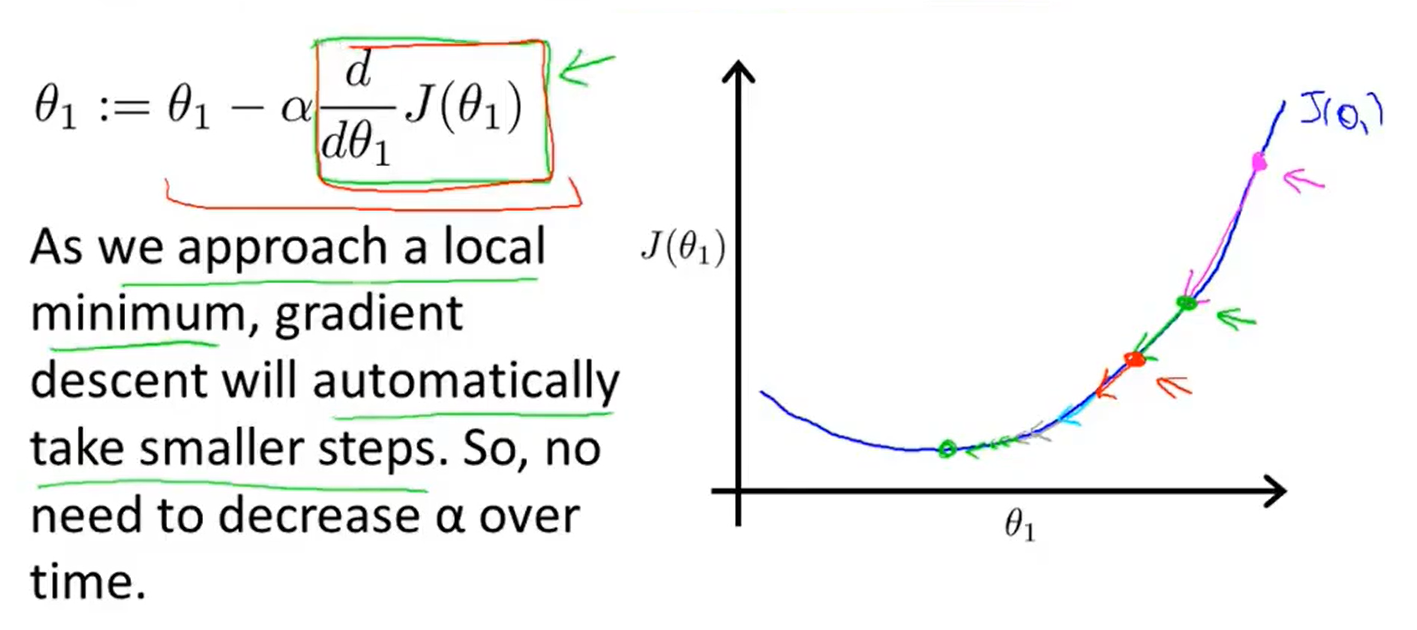
- Gradient descent can converge to a local minimum, even with the learning rate α fixed

 在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。
在统计学中,线性回归(Linear Regression)是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。