无标度网络模型

小世界网络模型是一种典型的均匀网络，其节点度分布类似于泊松分布，说 明在现实中大多数人都拥有差不多规模的社交圈。但是在现实中的许多网络中， 比如互联网，有些活跃用户的社交圈是远远大于非活跃用户的，并且活跃用户也 往往具有更高的话语权和影响力。在 Barabasi 等研究者对其互联网等拓扑结构的 研究时发现， 万维网、演员合作网络以及电力网络的度分布均符合幂律分布。

1999 年 10 月，Barabasi 与 Albert 在《Science》上发表了《Emergence of Scaling in Random Networks》，提出了无标度网络，其具体构建方法如下：

1、 增长：网络的规模是不断增加的，若有一个包含m₀个节点的连通网络，之后每新增一个节点就将该节点连接到已存在的m个节点上，且有m ≤ m₀

2、 优先连接：一个新节点与一个已存在的节点i连接的概率为Π_i，并且节点i的连接概率与该节点度k_i有关：

BA无标度网络演化的过程如下图所示。

若一个 BA 无标度网络含有 N 个节点，其度分布符合：

平均路径长度：

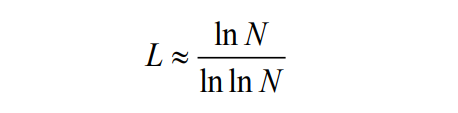
聚类系数：

可以看出，BA 无标度网络的度分布函数可用指数为 3 的幂律函数表示。从 聚类系数与平均路径长度中可知，当节点数渐渐增多时，BA 无标度网络的聚类特性并不明显，但具有小世界特性。