二次型可逆线性变换的两道真题
真题最后的总结
一、题目1
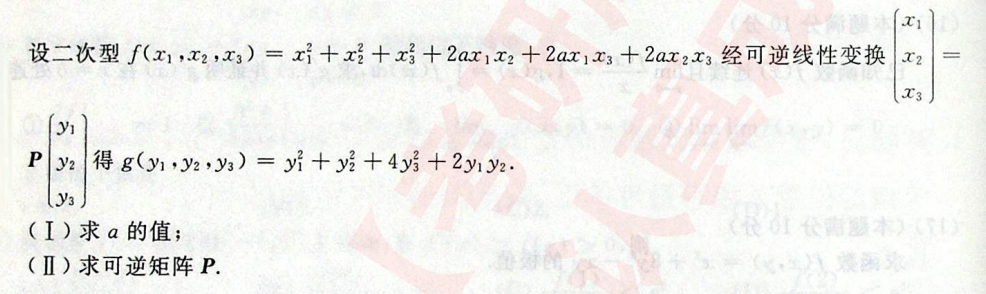
第一问：
运用合同的充要条件可以解出：
同样这里还可以写出f和g的分别的二次型矩阵，分别记为A和B，由r(A)=r(B)=2<3，则不满秩，|A|=0，但此时解出a有两个不同值，需要反代回矩阵检验r(A)
第二问：
本题思路：
同时考察配方法，何为配方法？复习一下讲义知识：
二、题目2
第一问：
这里的一个考点为：实对称矩阵若合同，则一定相似
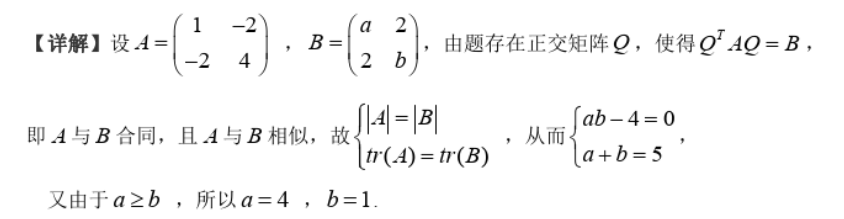
第二问：
唯一需要知道的：正交矩阵Q的转=Q的逆
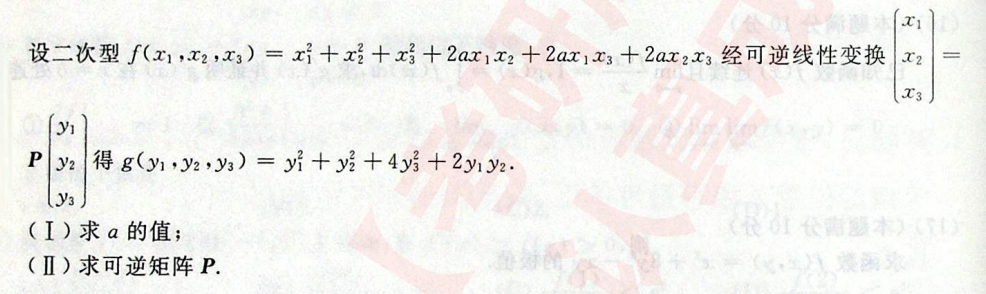
第一问：
运用合同的充要条件可以解出：
同样这里还可以写出f和g的分别的二次型矩阵，分别记为A和B，由r(A)=r(B)=2<3，则不满秩，|A|=0，但此时解出a有两个不同值，需要反代回矩阵检验r(A)
第二问：
本题思路：
同时考察配方法，何为配方法？复习一下讲义知识：
第一问：
这里的一个考点为：实对称矩阵若合同，则一定相似
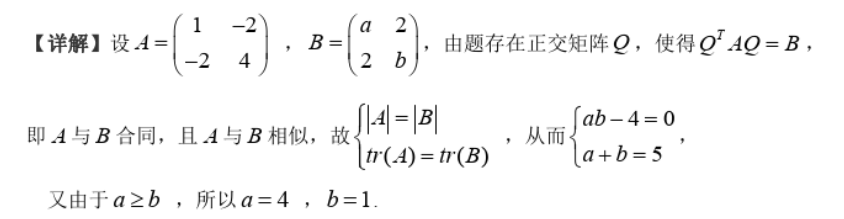
第二问：
唯一需要知道的：正交矩阵Q的转=Q的逆
