二叉树遍历序列还原

二叉树的遍历序列还原需要两个序列来确定，其中中序序列是必不可少的，这里根据真题,介绍的是利用中序和后序序列还原，中序和前序还原方法类似。

如果子树非空的情况下，中序遍历的特点是先遍历左子树，再输出父节点，再遍历右子树。 后序遍历的特点是先遍历左子树和右子树，最后输出父节点，整个过程是递归进行的。

根据这样的特点，我们可以得知，对于后序序列，最后一个输出的肯定是整棵树的根节点。而对于中序序列，每一个父节点的左边输出的节点一定是左子树上的节点，右边输出的节点一定是右子树上的节点。

有了这样的特点，我们就可以把还原分成左子树和右子树来递归进行。

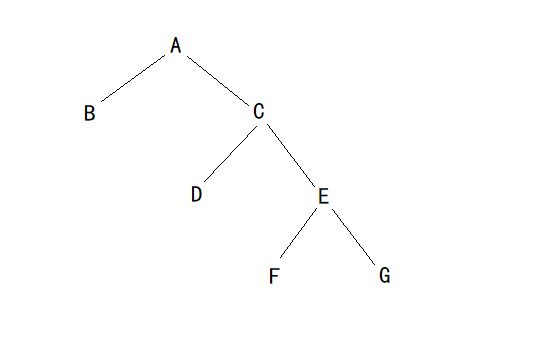
对于样例，还原步骤如下

图例：左子树 父节点 右子树

step1:从后往前遍历后序序列，第一个元素为a，说明为根节点

​ b a dcfeg

step2:第二个元素为c，a的右子树指向c

​ d c feg

step3:第三个元素为e，c的右子树指向e

​ f e g

step4:第四个元素为g，e的右子树指向g，没有左右子树了，停止。

这是dfs树右子树的一支，对左子树的操作类似。

经过这样一系列操作，最后就能复原整棵二叉树。