Taylor公式原来可以这么简单
1、Taylor公式
解决:含有高阶导数的中值定理或定积分、极限运算等题目
条件:f(x)在x=x0领域内(n+1)阶可导
结论:f(x)=Pn(x)+Rn(x)
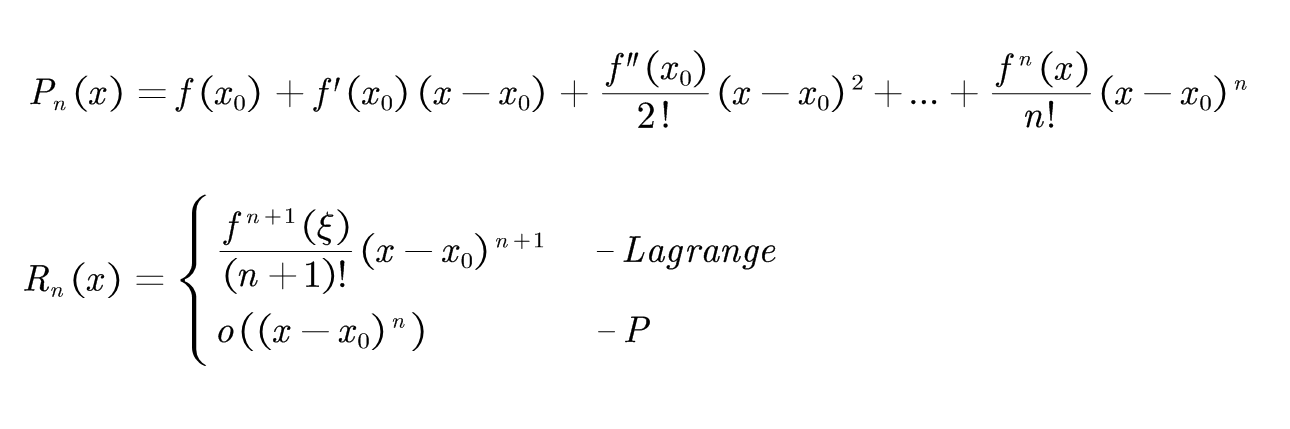
2、x和x0的取值

3、Taylor在中值定理中的运用
如下情况我们可以尝试使用(或Lagrange完全用不了):
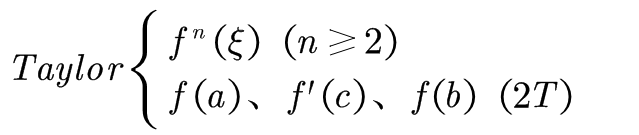





或给定f(x)及区间[a,b],将f(a)、f(b)分别在(a+b)/2处展开或将f((a+b)/2)分别在a、b两处展开,要根据证明结果来判断怎样展开。


可见完成步骤如下:
- 分析要使用Taylor
- 写出泰勒公式(一般都是Lagrange形式)
- 根据情况,使用加减、绝对值、介值定理等条件归纳
- 整合得出证明成立
4、Taylor在定积分中的运用
如下情况我们可以尝试使用:






可见完成步骤如下:
- 分析要使用Taylor,用f还是F
- 写出泰勒公式(一般都是Lagrange形式)
- 根据情况,使用积分、加减、绝对值、介值定理等条件归纳
- 整合得出证明成立
5、Taylor在极限中的运用
就是我们俗称的泰勒公式(皮亚诺形式),记住如下自推即可:
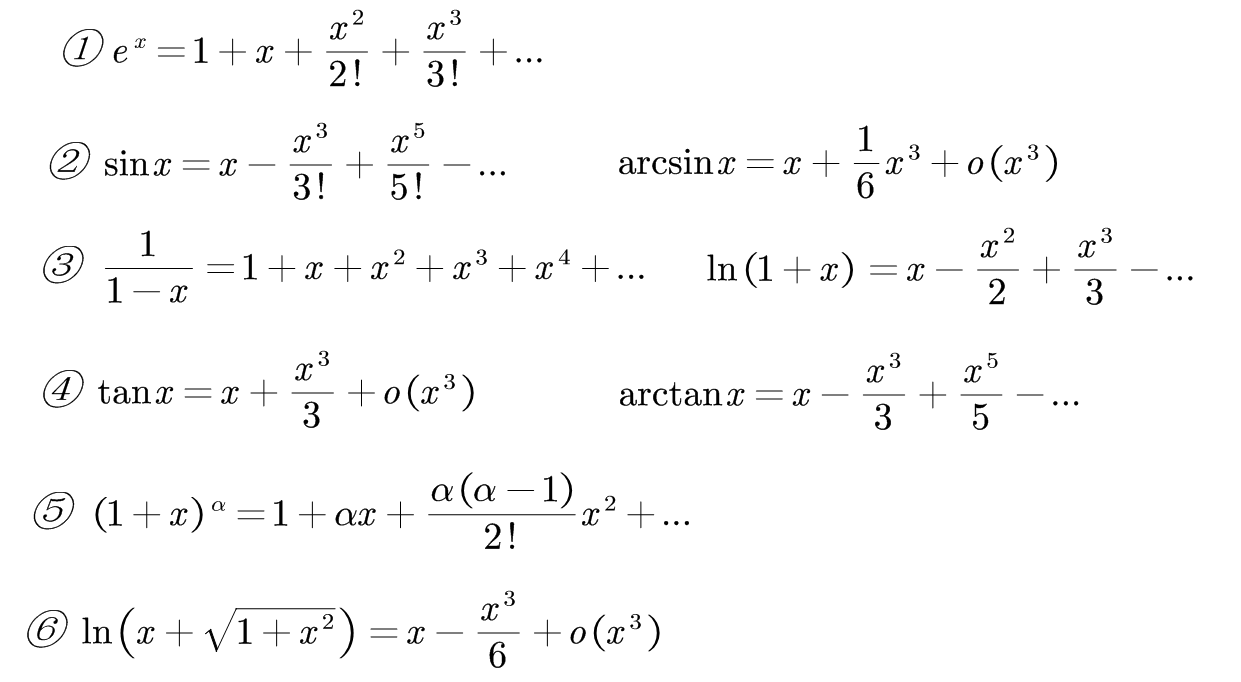
极大程度简化了极限的运算,展示一道题有兴趣可以算一下(答案可以百度哈)
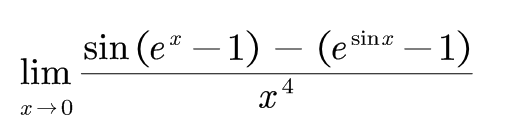
先写到这,还会有补充。

 把Taylor公式做了个总结,原来还是可以很简单的嘛!
把Taylor公式做了个总结,原来还是可以很简单的嘛!

