动态查找操作

在查找表中做查找操作的同时进行插入数据或者删除数据的操作，称此类表为动态查找表。

一、二叉排序树

二叉排序树（Binary Sort （Search） Tree也称为 二叉搜索树）要么是空二叉树，要么具有如下特点：

• 二叉排序树中，如果其根结点有左子树，那么左子树上所有结点的值都小于根结点的值；
• 二叉排序树中，如果其根结点有右子树，那么右子树上所有结点的值都大于根结点的值；
• 二叉排序树的左右子树也要求都是二叉排序树

由上可观：二叉排序树的定义本身依赖于递归思想

如下图所示，即为一个二叉排序树：

1、动态操作

查找操作：

由于二叉排序树的特点:(左子树<根结点<右子树),所以每次查找一个关键字，需要先和根结点进行比较：

如果这个关键字小于根结点的值，则再到这个根结点的左子树进行同样的比较操作一直进行下去直到找到该关键字，表示查找成功，或者是空指针，表示查找失败。

如果这个关键字大于根结点的值，则再到这个根结点的右子树进行同样的比较操作一直进行下去直到找到该关键字，表示查找成功，或者是空指针，表示查找失败。

插入操作：

①空树：直接插入新结点返回成功

②树不空：检查是否存在关键字重复的结点：

​ a.存在：返回插入失败

​ b.不存在：检查根结点的值和待插入关键字值的大小关系递归插入左右子树

删除操作：

①删除的是叶子结点 方法：直接删去该结点即可

②删除的是仅有左子树或者右子树的结点 方法：子承父业

③删除的是左右子树都有的结点 方法：进行中序遍历，找到待删除结点的直接前驱或者直接后继结点，用该结点来替换待删除结点，再删除该结点。

第三种情况（难点）图解：

2、Java代码实现

主要看删除操作，原作者：CSDN-梅森上校 在此补齐了一些注释。

定义树节点

copy
package DEMO.BinarysearchtreeDemo;

public class TreeNode<E> {
    E element;
    TreeNode<E> parent;        //父节点
    TreeNode<E> leftChild;    //左孩子 
    TreeNode<E> rightChild;  //右孩子

    public TreeNode(E element, TreeNode<E> parent) {
        this.element=element;
        this.parent=parent;
    }

    public TreeNode(){}

    //Alt+insert quick get/set

    public E getElement() {
        return element;
    }

    public void setElement(E element) {
        this.element = element;
    }

    public TreeNode<E> getParent() {
        return parent;
    }

    public void setParent(TreeNode<E> parent) {
        this.parent = parent;
    }

    public TreeNode<E> getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(TreeNode<E> leftChild) {
        this.leftChild = leftChild;
    }

    public TreeNode<E> getRightChild() {
        return rightChild;
    }

    public void setRightChild(TreeNode<E> rightChild) {
        this.rightChild = rightChild;
    }
}

二叉排序树算法

copy
package BlueBridge.Chapter5.BinarysearchtreeDemo;

import java.util.Iterator;
import java.util.NoSuchElementException;

public class BinarySortTree<E> {
    //根节点
    private TreeNode<E> root = null;
    //树中元素个数
    private int size = 0;
    //空参构造
    public BinarySortTree() {}
    //统计二叉树中的结点
    public int countSize() {
        return size;
    }
    //获得结点元素值
    public E getRoot() {
        return root == null? null:root.element;
    }

    /**
     * 递归实现: 查找指定元素element是否在树中存在
     * ①空树：直接插入新结点返回成功
     * ②树不空：检查是否存在关键字重复的结点：
     *          a.存在：返回插入失败
     *          b.不存在：检查根结点的值和待插入关键字值的大小关系递归插入左右子树
     * @param t 表示从此节点开始往下查找
     * @param element 指定要查找的元素
     * @param f 保存t的父节点
     * @param p 若查找成功p指向此数据元素节点，否则返回查找路径上的最后一个节点
     * @return 在则true 不在则false
     */
    private boolean searchBST(TreeNode<E> t, Object element, TreeNode<E> f, TreeNode<E> p) {
        if (t==null) {
            p = f;
            return false;
        }
        Comparable<? super E > e =(Comparable<? super E>) element;
        int cmp = e.compareTo(t.element);
        if (cmp < 0) {
            return searchBST(t.leftChild, element, t, p);
        } else if (cmp > 0) {
            return searchBST(t.rightChild, element, t, p);
        } else {
            p = t;
            return true;
        }
    }

    /**
     * 非递归实现 ，学习一下就行
     * @param element 指定要查找的元素
     * @param p 若查找成功p指向此数据元素节点，否则返回查找路径上的最后一个节点
     * @return 在则true 不在则false
     */
    private boolean searchBST_2(Object element, TreeNode<E>[] p) {
        Comparable<? super E> e = (Comparable<? super E>) element;
        TreeNode<E> parent = root;
        TreeNode<E> pp = null;
        // 保存parent父节点
        while (parent != null) {
            int cmp = e.compareTo(parent.element);
            pp = parent;
            if (cmp < 0) {
                parent = parent.leftChild;
            } else if (cmp > 0) {
                parent = parent.rightChild;
            } else {
                p[0] = parent;
                return true;
            }
        }
        p[0] = pp;
        return false;
    }

    /**
     * 插入操作
     * @param element 指定要查找的元素
     * @return element已在二叉树中返回false，否则如果找不到指定元素，进行插入动作后返回true
     */
    public boolean add(E element) {
        TreeNode<E> t = root;
        if (t == null) {
            // 如果根节点为空
            root = new TreeNode<E>(element, null);
            size = 1;
            return false;
        }
        Comparable<? super E> e = (Comparable<? super E>) element;
        TreeNode[] p = new TreeNode[1];
        if (!searchBST_2(element, p)) {
            // 查找失败，插入元素
            TreeNode<E> s = new TreeNode<E>(element, p[0]);
            int cmp = e.compareTo((E) p[0].element);
            if (cmp < 0) {
                p[0].leftChild = s;
            }
            if (cmp > 0) {
                p[0].rightChild = s;
            }
            size++;
            return true;
        }
        return false;
    }

    /**
     *  移除节点，同时调整二叉树使之为二叉排序树 实现原理：
     *  假设要删除的节点为p，其父节点为f，而p是f的左节点 分三种情况讨论:
     *      1.若p为叶子节点，直接删除
     *      2.若p有只有一个左孩子或者一个右孩子，则删除p，使PL或者PR为f的左子树
     *      3.若p的左右子树均不为空，由二叉排序树的特点可知在删除p前，中序遍历此二叉树
     *      可以得到一个有序序列，在删去p后为了保持其他元素的相对位置不变，可以这样做：
     *      令p的直接前驱(或直接后继)替代p，然后删除其直接前驱或直接后继。其直接前驱可由 中序遍历的特点获得
     *
     * @param o 要移除的结点
     * @return 查找到该节点 移除后返回true ，否则返回false
     */
    public boolean remove(Object o) {
        TreeNode<E>[] p = new TreeNode[1];
        if (searchBST_2(o, p)) {
            deleteTreeNode(p[0]); // 查找成功，删除元素
            return true;
        }
        return false;
    }

    private void deleteTreeNode(TreeNode<E> p) {
        size--;
        if (p.leftChild != null && p.rightChild != null) {
            // 如果p左右子树都不为空，找到其直接后继，替换p
            TreeNode<E> s = successor(p);
            p.element = s.element;
            p = s;
        }
        TreeNode<E> replacement = (p.leftChild != null ? p.leftChild : p.rightChild);

        if (replacement != null) { // 如果其左右子树有其一不为空
            replacement.parent = p.parent;
            if (p.parent == null) // 如果p为root节点
                root = replacement;
            else if (p == p.parent.leftChild) // 如果p是左孩子
                p.parent.leftChild = replacement;
            else
                p.parent.rightChild = replacement; // 如果p是右孩子

            p.leftChild = p.rightChild = p.parent = null; // p的指针清空

        } else if (p.parent == null) { // 如果全树只有一个节点
            root = null;
        } else { // 左右子树都为空,p为叶子节点
            if (p.parent != null) {
                if (p == p.parent.leftChild)
                    p.parent.leftChild = null;
                else if (p == p.parent.rightChild)
                    p.parent.rightChild = null;
                p.parent = null;
            }
        }
    }

    /**
     *
     * @return 以中序遍历方式遍历树时，t的直接后继 （主要处理第三种情况）
     */
    static <E> TreeNode<E> successor(TreeNode<E> t) {
        if (t == null)
            return null;
        else if (t.rightChild != null) {
            TreeNode<E> p = t.rightChild; // 往右，然后向左直到尽头
            while (p.leftChild != null)
                p = p.leftChild;
            return p;
        } else { // rightChild为空，如果t是p的左子树，则p为t的直接后继
            TreeNode<E> p = t.parent;
            TreeNode<E> ch = t;
            while (p != null && ch == p.rightChild) {
                ch = p; // 如果t是p的右子树，则继续向上搜索其直接后继
                p = p.parent;
            }
            return p;
        }
    }

    public Iterator<E> itrator() {
        return new BinarySortIterator();
    }

    /**
     * 返回中序遍历此树的迭代器
     */
    private class BinarySortIterator implements Iterator<E> {
        TreeNode<E> next;
        TreeNode<E> lastReturned;

        public BinarySortIterator() {
            TreeNode<E> s = root;
            if (s != null) {
                while (s.leftChild != null) {
                    s = s.leftChild; // 找到中序遍历的第一个元素
                }
            }
            next = s; // 赋给next
        }

        @Override
        public boolean hasNext() {
            return next != null;
        }

        @Override
        public E next() {
            TreeNode<E> e = next;
            if (e == null)
                throw new NoSuchElementException();
            next = successor(e);
            lastReturned = e;
            return e.element;
        }

        @Override
        public void remove() {
            if (lastReturned == null)
                throw new IllegalStateException();
            if (lastReturned.leftChild != null && lastReturned.rightChild != null)
                next = lastReturned;
            deleteTreeNode(lastReturned);
            lastReturned = null;
        }
    }

    // 测试代码
    public static void main(String[] args) {
        BinarySortTree<Integer> tree = new BinarySortTree<Integer>();
        tree.add(62);
        tree.add(15);
        tree.add(68);
        tree.add(12);
        tree.add(46);
        tree.add(65);
        tree.add(79);
        tree.add(35);
        tree.add(57);


        System.out.println("root=" + tree.getRoot());
        System.out.println("二叉树的中序遍历：");
        Iterator<Integer> it = tree.itrator();
        while (it.hasNext()) {
            System.out.print(it.next()+"\t");
        }
        System.out.println();
        System.out.println(tree.countSize());
// 省略前面的代码
// 一个add插入操作
//        System.out.println("插入一个节点 53");
//        tree.add(53);
//        System.out.println("root=" + tree.getRoot());  
//        System.out.println("二叉树的中序遍历：");
//        Iterator<Integer> it2 = tree.itrator();  
//        while (it2.hasNext()) {  
//            System.out.print(it2.next()+"\t");  
//        }  
//        System.out.println();
//        System.out.println(tree.countSize()); 
    }
}

3、性能分析

二叉排序树的性能和二叉排序树的高度有关，或者说和二叉排序树的形状有关

4、一道例题

二、平衡二叉树（AVL树）

平衡二叉树(AVL树)是特殊的二叉排序树，特殊的地方在于左右子树的高度之差绝对值不超过1，而且左右子树又是一棵平衡二叉树。

其实就是在二叉树的基础上，若树中每棵子树都满足其左子树和右子树的深度差都不超过 1，则这棵二叉树就是平衡二叉树。

• 这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(log2N)。

• 定义结点左子树与右子树的高度差为该结点的平衡因子，则平衡二叉树结点的平衡因子的值只可是−1、0或1

• 查找过程和二叉排序树完全相同

如上图，其中 （a） 的两棵二叉树中由于各个结点的平衡因子数的绝对值都不超过 1，所以 （a） 中两棵二叉树都是平衡二叉树；而 （b） 的两棵二叉树中有结点的平衡因子数的绝对值超过 1，所以都不是平衡二叉树。

1、平衡化的实现

整个实现过程是通过在一棵平衡二叉树中依次插入元素(按照二叉排序树的方式)，若出现不平衡，则要根据新插入的结点与最低不平衡结点的位置关系进行相应的调整。分为LL型、RR型、LR型和RL型4种类型整理自CSDN作者-清塘荷韵_kathy和博客园作者-守攻，各调整方法如下(下面用A表示最低不平衡结点)：

（1）LL型调整：

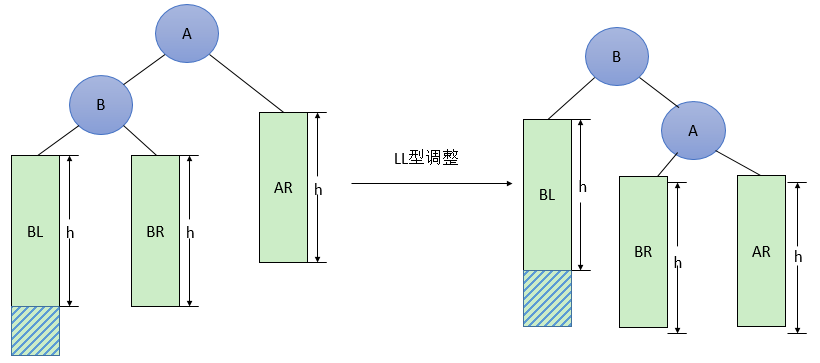
由于在A的左孩子(L)的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1增至2。下面图1是LL型的最简单形式。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B顺时针旋转一样。

LL型调整的一般形式如下图所示，表示在A的左孩子B的左子树BL(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

• 将A的左孩子B提升为新的根结点；

• 将原来的根结点A降为B的右孩子；

• 各子树按大小关系连接(BL和AR不变，BR调整为A的左子树)。

（2）RR型调整：

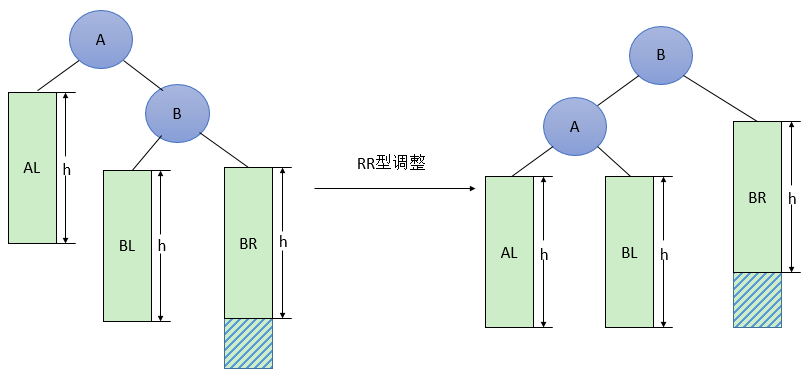
由于在A的右孩子(R)的右子树(R)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。下图是RR型的最简单形式。显然，按照大小关系，结点B应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡，A结点就好像是绕结点B逆时针旋转一样。

RR型调整的一般形式如下图所示，表示在A的右孩子B的右子树BR(不一定为空)中插入结点(图中阴影部分所示)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

• 将A的右孩子B提升为新的根结点；

• 将原来的根结点A降为B的左孩子；

• 各子树按大小关系连接(AL和BR不变，BL调整为A的右子树)。

（3）LR型调整：

由于在A的左孩子(L)的右子树(R)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由1变为2。下图是LR型的最简单形式。显然，按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。

LR型调整的一般形式如下图所示，表示在A的左孩子B的右子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

• 将C的右孩子B提升为新的根结点；

• 将原来的根结点A降为C的右孩子；

• 各子树按大小关系连接(BL和AR不变，CL和CR分别调整为B的右子树和A的左子树)。

（4）RL型调整：

由于在A的右孩子(R)的左子树(L)上插入新结点，使原来平衡二叉树变得不平衡，此时A的平衡因子由-1变为-2。下图是RL型的最简单形式。显然，按照大小关系，结点C应作为新的根结点，其余两个节点分别作为左右孩子节点才能平衡。

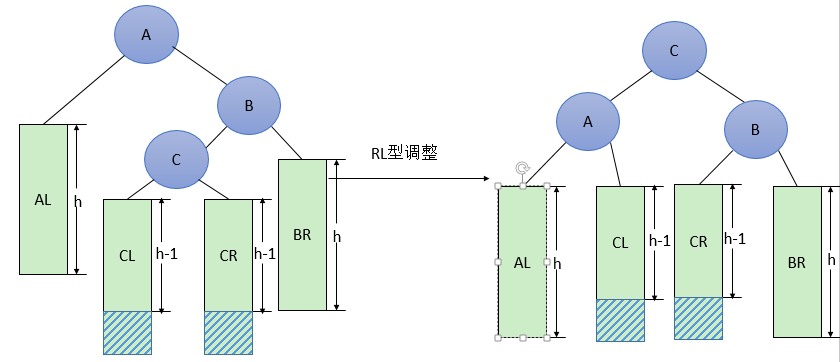
RL型调整的一般形式如下图所示，表示在A的右孩子B的左子树(根结点为C，不一定为空)中插入结点(图中两个阴影部分之一)而导致不平衡( h 表示子树的深度)。这种情况调整如下：

• 将C的右孩子B提升为新的根结点；

• 将原来的根结点A降为C的左孩子；

• 各子树按大小关系连接(AL和BR不变，CL和CR分别调整为A的右子树和B的左子树)。

平衡二叉树的深度接近logN的数量级，从而保证在二叉排序树上插入、删除和查找等操作的平均时间复杂度为O(logN)。

2、一道例题

首先学会找平衡因子，平衡因子看哪个值先为-2（哪个根左右子树或子树高度差超过1，这个根的平衡因子就为-2，并且如果有两个平衡因子-2的，旋转那个靠近插入值那边的那个根）

如上图所示案例，节点16的平衡因子为-2，产生了不平衡，因此从16开始调整

插入位置	如何调整
插入结点在发现者左子树的左边	LL调整，左单旋
插入结点在发现者右子树的右边	RR调整，右单旋
插入结点在发现者左子树的右边	LR调整，右左双旋
插入结点在发现者右子树的左边	RL调整，左右双旋

注意：在双旋过程中，注意不要让双旋的名称误解了，名称仅仅是表示插入结点相对于发现结点的位置，左右双旋是先右单旋在左单旋，右左双旋是先左单旋再右单旋

3、删除操作

平衡二叉树的删除也涉及到删除后的连接问题。其删除一般分为4种情况：整理自CSDN作者-别是清欢
1）删除叶子结点；
2）删除左子树为空，右子树不为空的结点：
3）删除左子树不为空，右子树为空的结点；
4）删除左右子树都不为空的结点。

删除叶子结点很简单，直接删除即可，此处不再赘述。

（1）左子树为空，右子树不为空

---

以图中的平衡二叉树为例。
现要删除结点105，结点105有右子树，没有左子树，则删除后，只需要将其父结点与其右子树连接即可。

删除结点会使相应子树的高度减小，可能会导致树失去平衡，如果删除结点后使树失去平衡，要调整最小不平衡子树使整棵树达到平衡。删除和插入一样，在删除的过程中要时刻保持树的平衡性。

（2）左子树不为空，右子树为空

---

要删除一个结点，结点有左子树没有右子树，这种情况与上一种情况相似，只需要将其父结点与其左子树连接即可。例如要删除图中的结点100，其删除过程如图所示：

（3）左右子树均不为空

---

如果要删除的结点既有左子树又有右子树，则要分情况进行讨论。

• 如果该结点x的平衡因子为0或者1 ，找到其左子树中具有最大值的结点max，将max的内容与x的元素进行交换，则max即为要删除的结点。由于树是有序的，因此找到的max结点只可能是一个叶子结点或者一个没有右孩子的结点。

例如现在有一棵平衡二叉树。现在要删除结点20，结点20的平衡因子是1，则在其左子树中找到最大结点15，将两个结点的数值互换。然后删除结点20。

在删除结点20之后，平衡二叉树失去了平衡，结点10的平衡因子为2，则需要对此最小不平衡子树进行调整，此次调整类似于插入，先进性一次左旋转再进行一次右旋转即可，调整后的结果如图：

• 如果要删除的结点其平衡因子为-1，则找到其右子树中具有最小值的结点min，将min与x的数据值进行互换，则min即为新的要删除的结点，将结点删除后，如果树失去了平衡，则需要重新调整。由于平衡二叉树是有序的，因此这样的结点只可能是一个叶子结点，或者是一个没有左子树的结点。