图的应用(二)——最短路径
本文很大一部分摘抄其他优质博客,因为考研时间有限,无时间仔细创作,但内容和代码绝对都是精挑细选且认真实验过,都很好理解。
一、最短路径
在带权图中源点到终点的多条路径中,寻找一条各边权值之和最小的路径,在非带权图中两点之间经过变数最少的路径,即最短路径。
我们平时坐地铁就是一个很好的实际问题:怎样才能最短的路途到达目的地呢?

二、迪杰斯特拉(Dijkstra)算法
主要思想:是以起始点为中心向外层层扩展,直到扩展到终点为止。更具体讲,是运用贪心思想实现的,首先把起点到所有点的距离存下来,然后找个最短的,然后松弛一次再找出最短的,所谓的松弛操作就是,遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近,如果更近了就更新距离,这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。
具体实现如下:
1.构建一个连通图如图

2.设置一个数组dist,以点A为起点进行搜索,初始化到各点距离是无穷大
A->B = 6,即dist[B] = 6;A->C = 3,即dist[C] = 3;最短路径为A->C;

3.把C当做起点,这时,A到B最短路径A->B = 5,A->D = 6,A->E = 7,修改数组

4.按照以上规则依次进行搜索



5.直到遍历到最后一个元素终止,即得出A到各点最短路径

Java代码实现:
public class Dijkstra {
/*
* 参数adjMatrix:为图的权重矩阵,权值为-1的两个顶点表示不能直接相连
* 函数功能:返回顶点0到其它所有顶点的最短距离,其中顶点0到顶点0的最短距离为0
*/
public int[] getShortestPaths(int[][] adjMatrix) {
int[] result = new int[adjMatrix.length]; //用于存放顶点0到其它顶点的最短距离
boolean[] used = new boolean[adjMatrix.length]; //用于判断顶点是否被遍历
used[0] = true; //表示顶点0已被遍历
for(int i = 1;i < adjMatrix.length;i++) {
result[i] = adjMatrix[0][i];
used[i] = false;
}
for(int i = 1;i < adjMatrix.length;i++) {
//用于暂时存放顶点0到i的最短距离,初始化为Integer型最大值
int min = Integer.MAX_VALUE;
int k = 0;
for(int j = 1;j < adjMatrix.length;j++) { //找到顶点0到其它顶点中距离最小的一个顶点
if(!used[j] && result[j] != -1 && min > result[j]) {
min = result[j];
k = j;
}
}
used[k] = true; //将距离最小的顶点,记为已遍历
for(int j = 1;j < adjMatrix.length;j++) {
//然后,将顶点0到其它顶点的距离与加入中间顶点k之后的距离进行比较,更新最短距离
if(!used[j]) { //当顶点j未被遍历时
//首先,顶点k到顶点j要能通行;这时,当顶点0到顶点j的距离大于顶点0到k再到j的距离或者顶点0无法直接到达顶点j时,更新顶点0到顶点j的最短距离
if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1))
result[j] = min + adjMatrix[k][j];
}
}
}
return result;
}
public static void main(String[] args) {
Dijkstra test = new Dijkstra();
int[][] adjMatrix = {{0,6,3,-1,-1,-1},
{6,0,2,5,-1,-1},
{3,2,0,3,4,-1},
{-1,5,3,0,2,3},
{-1,-1,4,2,0,5},
{-1,-1,-1,3,5,0}};
int[] result = test.getShortestPaths(adjMatrix);
System.out.println("顶点0到图中所有顶点之间的最短距离为:");
for(int i = 0;i < result.length;i++)
System.out.print(result[i]+" ");
}
}
//output
//
//顶点0到图中所有顶点之间的最短距离为:
//0 5 3 6 7 9
//最短距离就是9
详细图解(仍有迷惑可戳):

注意:Dijkstra算法只能应用于不含负权值的图。因为在大多数应用中这个条件都满足,所以这种局限性并没有影响Dijkstra算法的广泛应用。
其次,大家要注意把Dijkstra算法与寻找最小生成树的Prim算法区分开来。两者都是运行贪心法思想,但是Dijkstra算法是比较路径的长度,所以必须把起点到相应顶点之间的边的权重相加,而Prim算法则是直接比较相应边给定的权重。
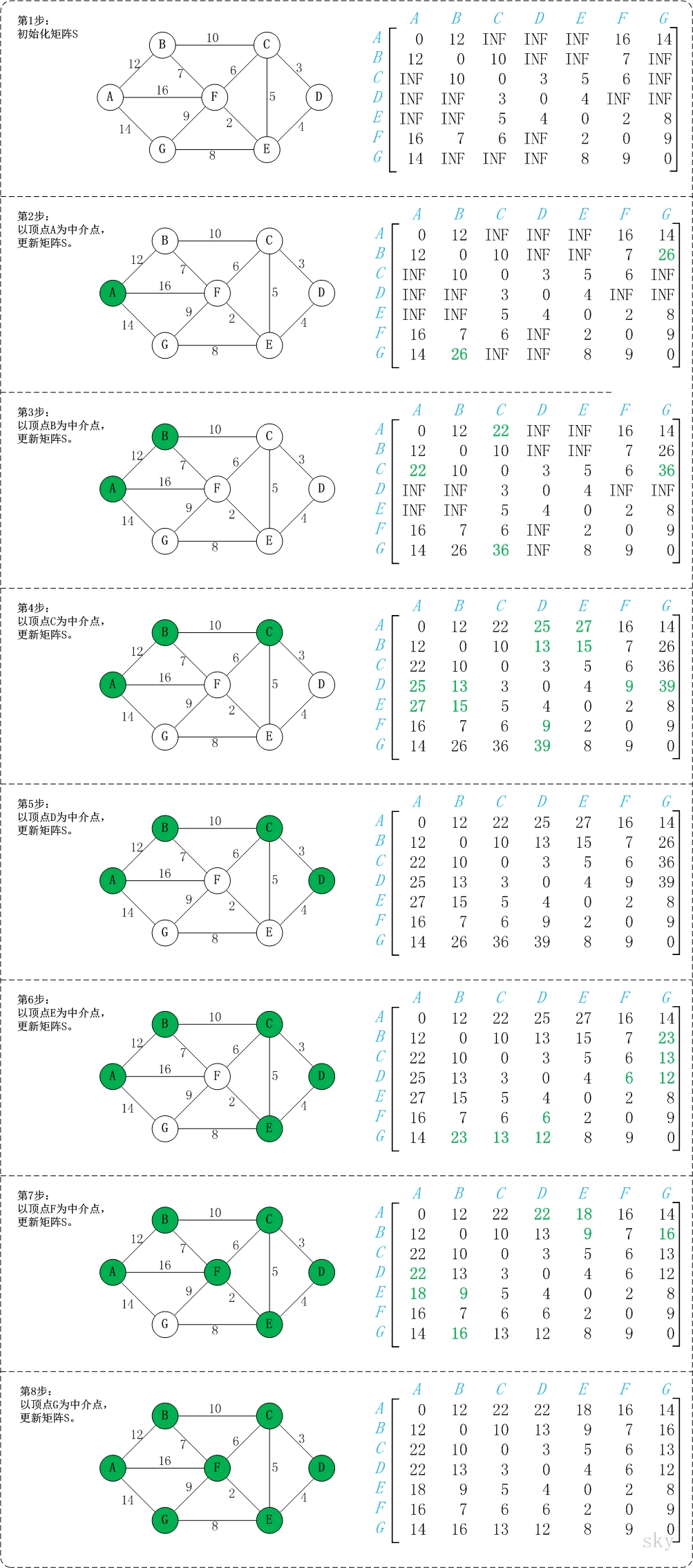
三、弗洛伊德(Floyd)算法
主要思想:将顶点i到j的直接距离依次与顶点i到顶点j之间加入k个中间节点之后的距离进行比较,从中选出最短的一组距离,即为顶点i到顶点j的最短距离,然后重复上述步骤求取其它顶点之间的最短距离。又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法。
具体实现如下:
以上图G4为例,来对弗洛伊德进行算法演示。
Java代码实现:
public class Floyd {
/*
* 参数adjMatrix:给定连通图的权重矩阵,其中权重为-1表示两个顶点不能直接相连
* 函数功能:返回所有顶点之间的最短距离权重矩阵
*/
public void getShortestPaths(int[][] adjMatrix) {
for(int k = 0;k < adjMatrix.length;k++) {
for(int i = 0;i < adjMatrix.length;i++) {
for(int j = 0;j < adjMatrix.length;j++) {
if(adjMatrix[i][k] != -1 && adjMatrix[k][j] != -1) {
int temp = adjMatrix[i][k] + adjMatrix[k][j]; //含有中间节点k的顶点i到顶点j的距离
if(adjMatrix[i][j] == -1 || adjMatrix[i][j] > temp)
adjMatrix[i][j] = temp;
}
}
}
}
}
public static void main(String[] args) {
Floyd test = new Floyd();
int[][] adjMatrix = {{0,-1,3,-1},
{2,0,-1,-1},
{-1,7,0,1},
{6,-1,-1,0}};
test.getShortestPaths(adjMatrix);
System.out.println("使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为:");
for(int i = 0;i < adjMatrix.length;i++) {
for(int j = 0;j < adjMatrix[0].length;j++)
System.out.print(adjMatrix[i][j]+" ");
System.out.println();
}
}
}
//output:
//
//使用Floyd算法得到的所有顶点之间的最短距离权重矩阵为:
// 0 10 3 4
// 2 0 5 6
// 7 7 0 1
// 6 16 9 0
注意,Floyd算法计算最短距离可以有负权值的边,但不能有权值和为负数的回路。
四、C语言核心代码
代码学习于王道数据结构,仅供参考。
1、Dijkstra
void Dijkstra(MGraph G,int v,int path[ ],int dist[ ]){ //v是源点的下标
int s[maxSize]; //数组s记录当前找到了到哪些顶点的最短路径 找到了对应值为1 没找的对应值为0
int i,j,min,u;
//初始化 将path dist s 数组的初值确定
for(i=0 ; i<G.vexnum ; i++){
dist[i]=G.edge[v][i]; //dist初值为源点到各个顶点的边的权值
s[i]=0; //一开始没有一个顶点
if(G.edge[v][i]<65535)path[i]=v; //与源点连通的顶点的path值存源点下标
else path[i]=-1;//刚开始到源点没有路径的顶点path值为-1
}
s[v]=1; //源点加入集合s
path[v]=-1; //源点不存在到自身的路径
//下面的循环中包含两部分作用:①内层第一个for循环是找到 到剩余顶点中距离最小的 顶点u 并把它加入最短路径②内层第二个for循环是由新加入的顶点u来判断是否找到了新的更短路径,如果有就更新,没有就不做任何操作
for(i=0;i<G.vexnum;i++){
min=65535;
for(j=0;j<G.vexnum;j++){
if(s[j]==0&&dist[j]<min){ //从剩余的顶点中找到距离最小的顶点
u=j;
//u用于保存当前找到的距离最小的顶点下标 当循环结束u保存的就是最小距离的顶点下标
min=dist[j];
}
}
s[u]=1;//到u的距离是最小的,所以把顶点u加入最短路径
for(j=0;j<G.vexnum;j++){
if(s[j]==0 && dist[u]+G.Edges[u][j]<dist[j]){
dist[j]=dist[u]+G.Edges[u][i];
//如果由新加入最短路径的顶点u到其他剩余顶点的距离变短了则
//修改到剩余顶点的距离为较小值
path[j]=u;//这条较短的路径是由顶点u过来的
}
}
}
}
时间复杂度:迪杰斯特拉算法的核心部分在于一个双重循环,这个双重循环的内循环又是两个并列的单重for循环组成(找距离最小顶点和更新距离),任意取其中一个循环中的操作为基本操作,都可以得出迪杰斯特拉算法的时间复杂度为O(n²) 其中n为图中的顶点数。
2、Floyd
void Floyd(MGraph G,int Path[][]){
int i, j, k ;
int A[MaxSize][MaxSize];
//对数组A[][]和Path[][]进行初始化
for(i=0; i<G.vexnums; i++){
for(j=0; j<G.vexnums; j++){
A[i][j]=G.Edges[i][j];
Path[i][j]=-1;
}
}
for(k=0; k<G.vexnums; k++){
for(i=0; i<G.vexnums; i++){
for(j=0; j<G.vexnums; j++){
if(A[i][j]>A[i][k]+A[k][j]){//如果顶点i到顶点j的距离比顶点i经过顶点k到顶点j的距离长,则更新从顶点i到顶点j的距离为较小值,并且存储k表示路径经过顶点k
A[i][j]=A[i][k]+A[k][j];
Path[i][j]=k;
}
}
}
}
}
弗洛伊德算法的核心为一个三重循环,所以时间复杂度为O(n³) 其中n是图中的顶点数。

 本篇重点掌握Dijkstra算法即可。
本篇重点掌握Dijkstra算法即可。